表面张力是什么？表面张力沿着什么方向？

表面张力。

· Part 1：力，不是简单的拉拉扯扯 ·

熟悉物理的朋友们一定很熟悉身边的力：重力、弹力、支持力、库仑力……每提到一个力的名字，脑海中大都可以浮现出一幅示意图，其中相互作用的两个物体之间你推我搡、你拉我扯。

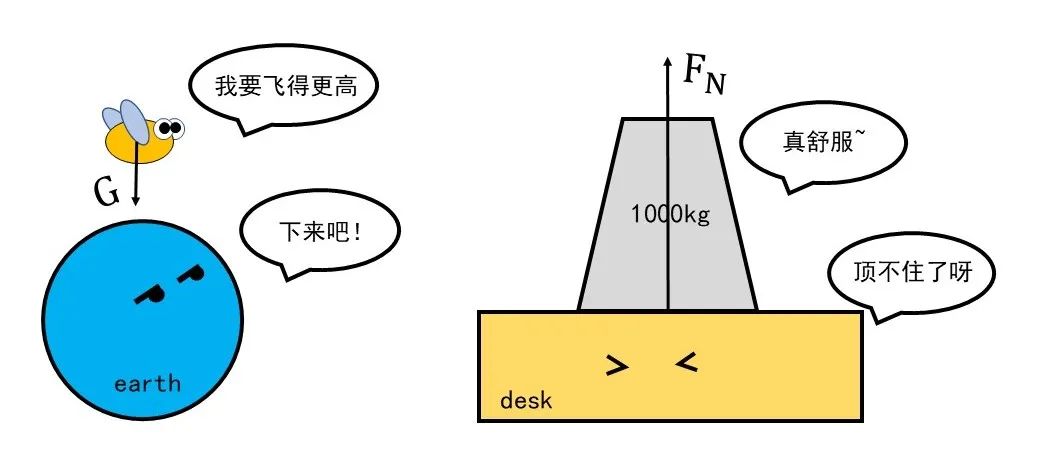
图1 重力与支持力示意

这样的理解虽然直观，但是缺少了几分更加深入的视角，也没办法真正理解什么是表面张力。那怎么办呢？我们来看看与力对应的能量（特指势能）。以重力为例，大家可能听说过重力势能，即某一地球附近的物体由于处于一定的高度而蕴含的能量。更加直观地讲，如果以地面为势能零点，则物体在重力的作用下下落到地面所能释放的能量就是重力势能。

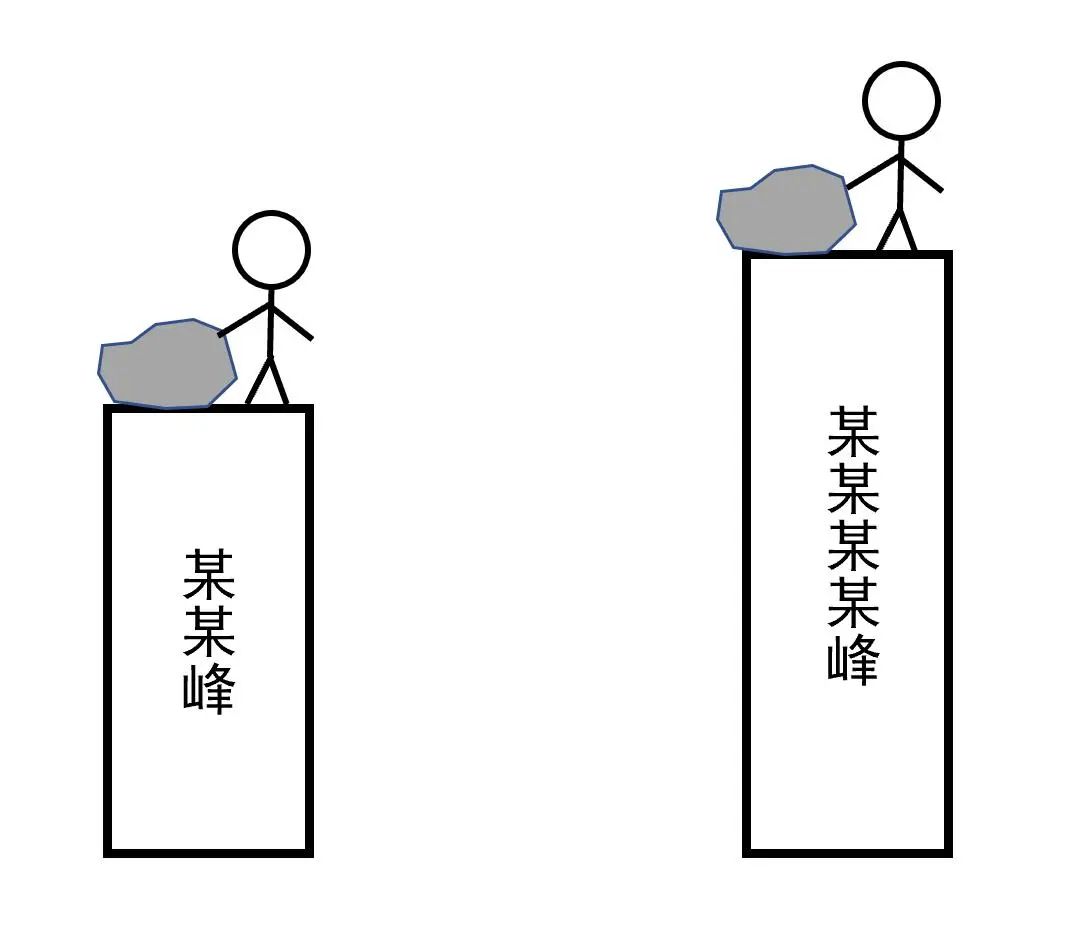
图2 重力势能的对比

如图2所示，如果小编从相对低一些的某某峰和高一些的某某某某峰推下一块同样的石头，哪个释放的重力势能大呢？很显然是从高一些的某某某某峰更大。那么，大了多少呢？

如果忽略重力随高度的变化，即认为石头的重力是一个常量G，那么答案是：

其中dL为两峰之间的高度差。稍加变形，我们就得到

这说明，重力是每升高单位高度带来的重力势能的变化！类似的，弹簧弹力是每拉长单位长度所带来的弹性势能的变化，分子间作用力是分子间距离每变化单位长度所带来的体系势能的变化……原来，与任意的势能对应的力都可以这样理解。

此时，小编优雅地问道：那么，表面张力是什么？

读者齐声答道：表面每增长单位面积而带来的表面能的变化！

小编鼓掌后追问：表面能是什么？表面张力沿着什么方向？

读者沉默，向小编投来期待的目光……

·Part 2：张力，不过是吹个泡泡 ·

其实，上面所谈及的问题可以很直观地从量纲看出来。我们都接触过做功的概念，功的单位和能量一样，都是焦耳J。而功是物体受到的某个力（单位为N）与物体在力的方向上移动的距离（单位为m）的乘积，即：1 J = 1 N·m。那么，力的单位除了N还可以写作 J/m，即每移动1m所引起的能量的变化。

然而有一种物理量的量纲是J/m2，它代表着每单位面积蕴含的能量，这个物理量便是比表面能。比表面能是一个涉及分子间作用的概念，我们需要从微观去认识。

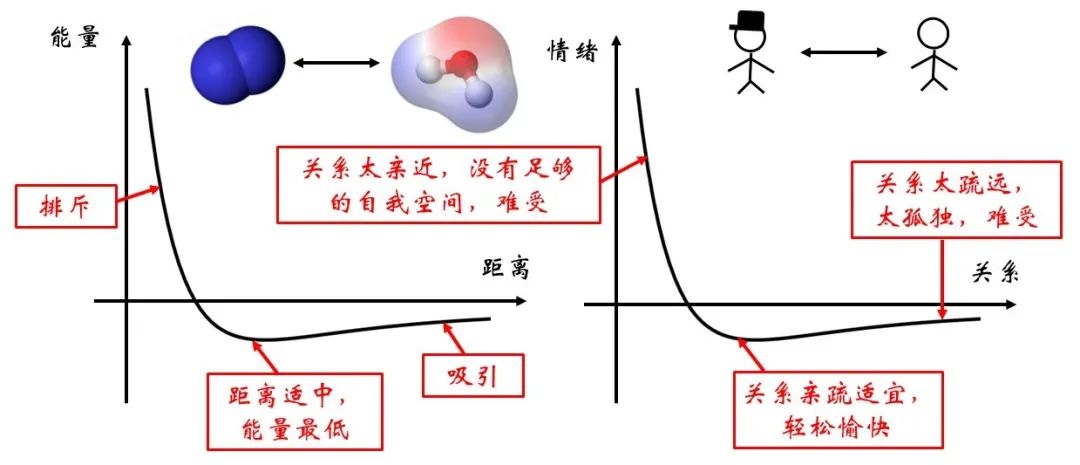
图3 氮气与水分子间作用势能的图示

在微观世界存在着多种多样的分子，比如上图所示的氮气与水分子。分子间组成的体系的势能与分子间的距离有关。这种关系正如两个人之间的关系，远了近了都不好。如果距离太近，彼此之间没了自我空间，情绪会不稳定，因此会产生相互排斥的作用；如果距离太远，每个人都太孤独，便会相互思念，彼此吸引。当彼此的距离恰到好处，便对应着能量的最低点，较为稳定。

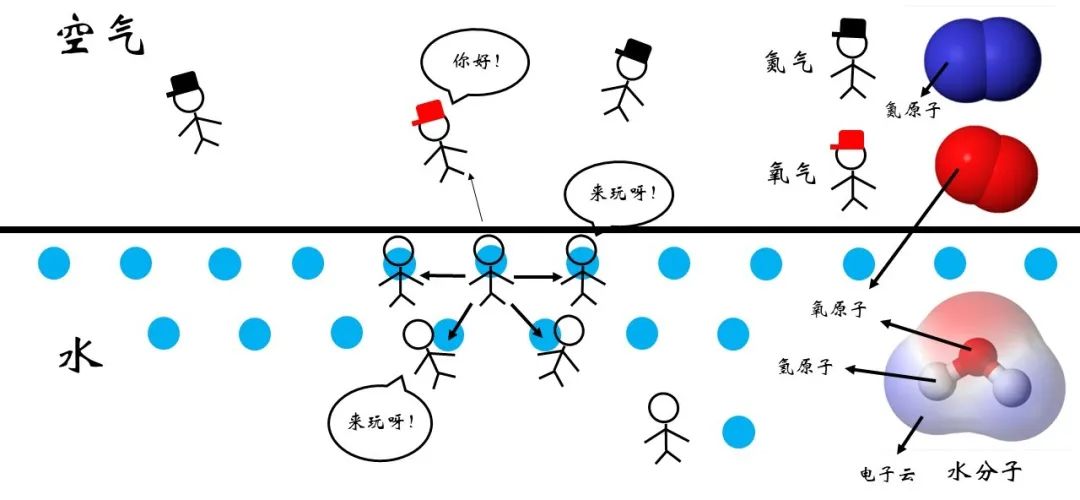
图4 水-空气界面示意

然而，这种关系的稳定程度是与双方分子的种类有关的。如图4所示，对于水-空气的界面而言，处于表面的水分子周围的分子种类较为丰富，除了其他水分子，还有空气中的氧气、氮气等分子。

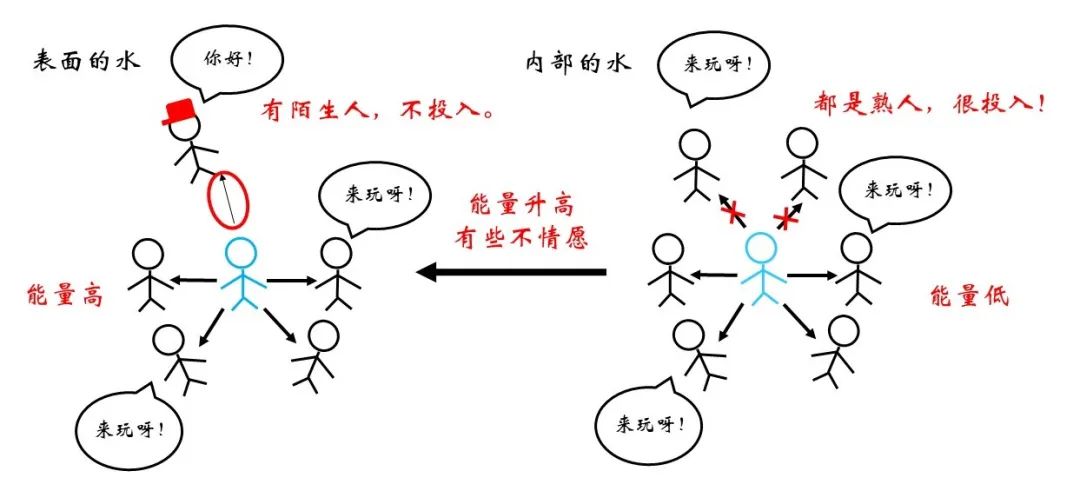
图5 内部与表面水对比

俗话说“物以类聚，人以群分”，更加相似的同类分子间往往关系更为融洽，而不同种分子间的关系则相对疏远。在物理上表现为同类分子间的势能曲线最低点更低。因此，对于一个存在于内部的水分子，如果来到表面，需要断开与同类分子的部分关系，而代之以与比较“生疏”的空气分子间的作用，显然是不情愿的！这体现为能量的升高。那么，什么情况下水分子要从内部来到表面呢？正是吹泡泡的时候。

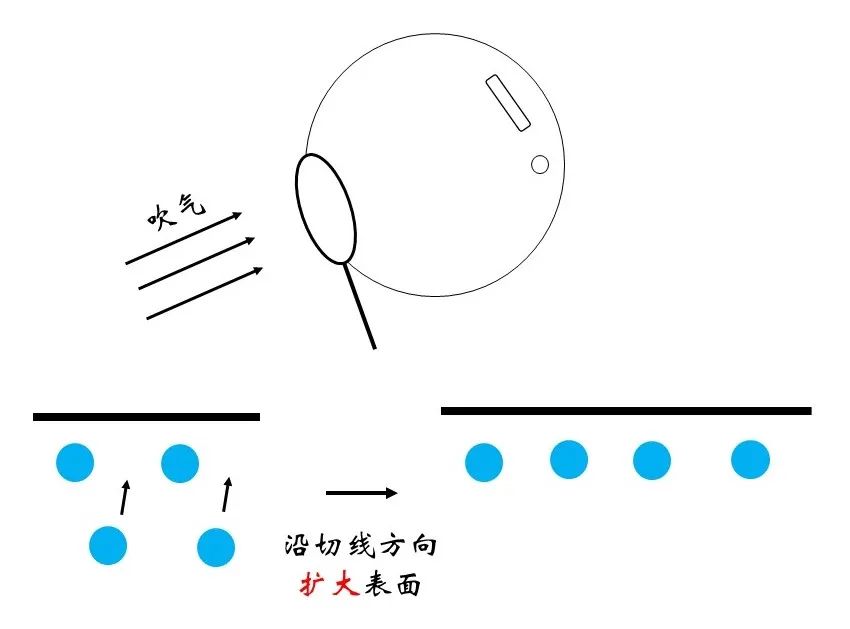
图6 吹泡泡过程示意

用圆环蘸一些肥皂水，肥皂水的体积是基本恒定的。当我们吹入空气使泡泡的表面积变得更大，自然泡泡的厚度会变薄。进一步解释就是，一定会有更多的水分子从内部来到表面，而这个过程是内部分子所不情愿的，因此会带来能量的升高。那么，表面每扩展单位的面积带来的能量升高是多少？这个数值正是比表面能。

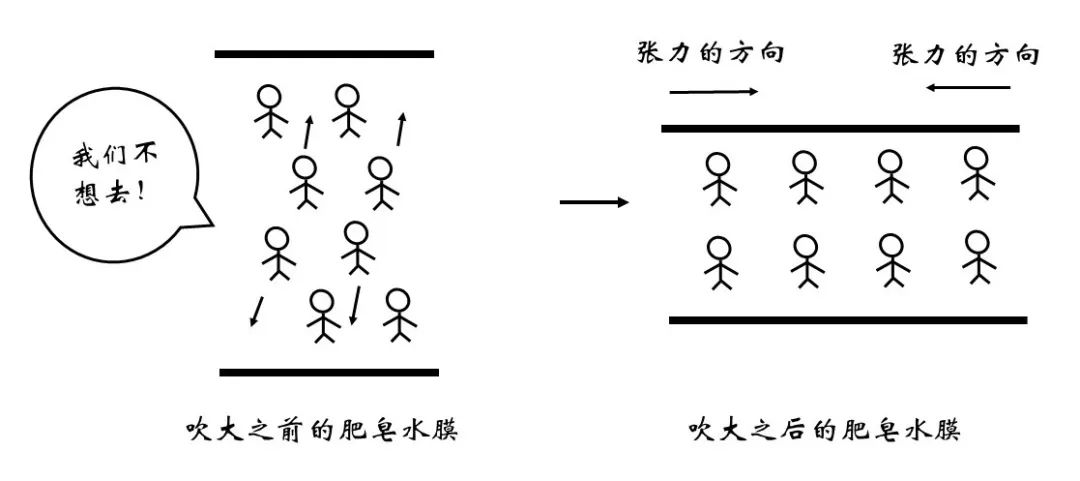
图7 表面的增大伴随肥皂泡变薄

我们曾经提到比表面能的单位是J/m2，而将这个物理量从力的角度去理解对于处理一些问题更加直观，我们常常将比表面能称为表面张力。而J/m2 = N/m，并不是力的单位N，因此表面张力代表的是作用在单位长度的表面上的力。在下图所示的实验中，肥皂水膜在力F的牵拉下长大，表面张力便是

其中，分母上的2来自于正反两侧都有表面的产生。

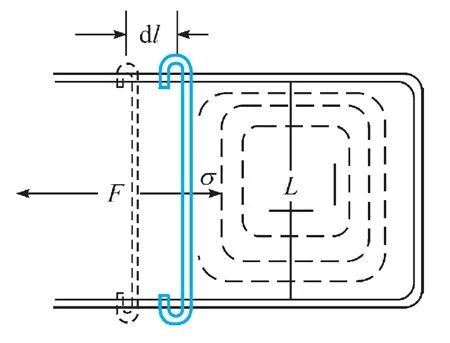
图8 表面张力实验示意图 | 图片源于【1】

那么表面张力的方向是什么呢？我们同样类比重力、弹力等力。简单回顾不难发现，如果将表面张力理解为单位面积形变引起的能量升高，那么对应的力应该指向使得能量降低的方向。对于表面张力，自然就是沿切线使得表面收缩的方向。

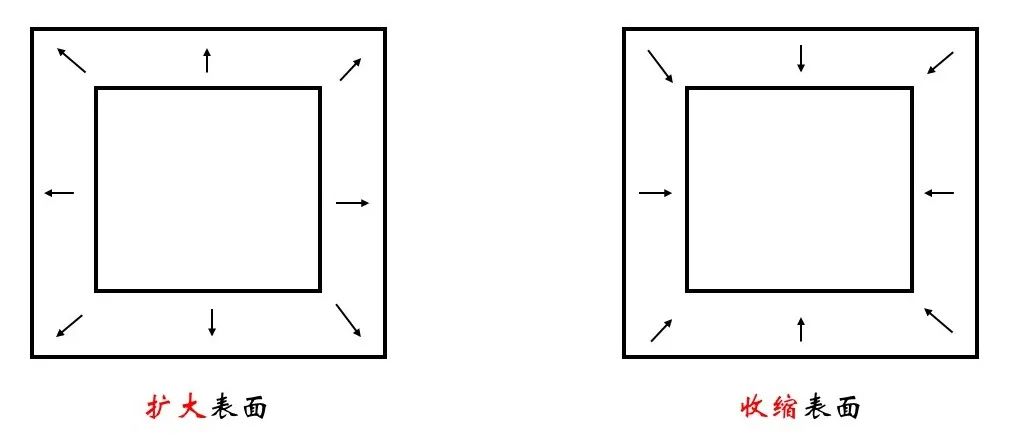
图9 表面张力的方向示意

· Part 3：追求球形，张力与重力之争 ·

在这一部分开始前，首先提出一个问题：在失重条件下，液滴会呈现什么形状？

稍加回忆，看过太空授课的读者应该都想起了那颗悬浮在太空中的球形水滴。

没错，失重环境下的液滴正是呈现球形，因为在一定的体积下，球体的表面积最小，因此球形液滴的总表面能最低。那么，在有重力的情况下呢？

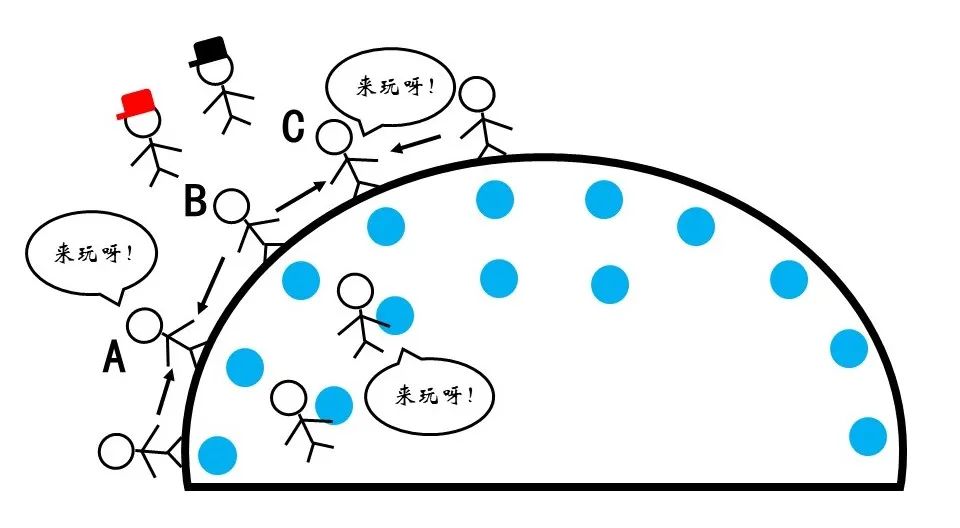
图11 表面分子有进入内部的趋势

在液滴的表面，每个分子都会受到沿切线的表面张力，效果上相当于每个分子（如A和C）都在拉周围的分子（如B）。B受到的周围表面分子的力的合力指向内部，有进入内部的趋势。这种张力的作用使得液滴尽可能维持着接近球形的状态，即拥有尽可能小的表面积。然而，重力起到另一种作用。

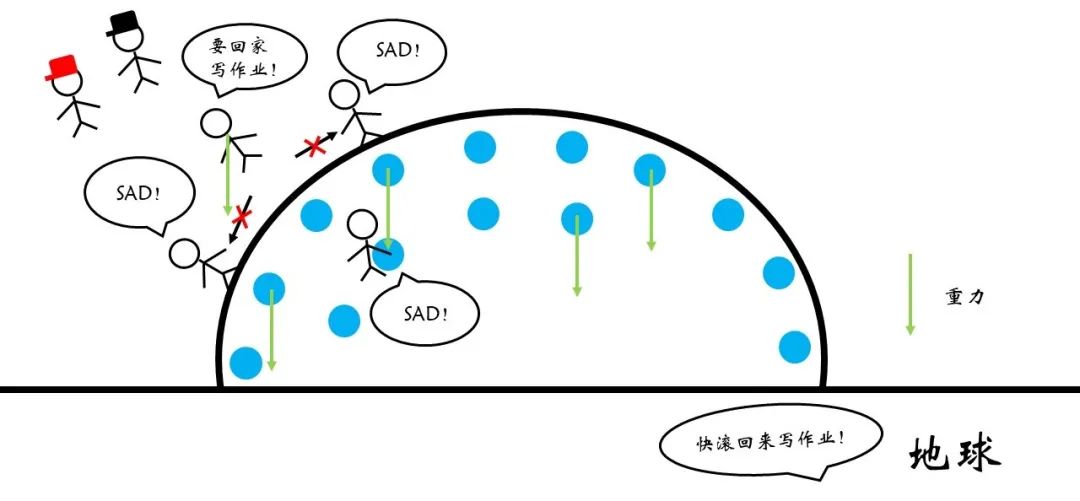
图12 重力的作用

重力的作用希望每个水分子都处在尽可能低的地方，显然呈现近似球形的形状并不是重力势能最低的情况。因此，表面张力与重力之间便存在着竞争。

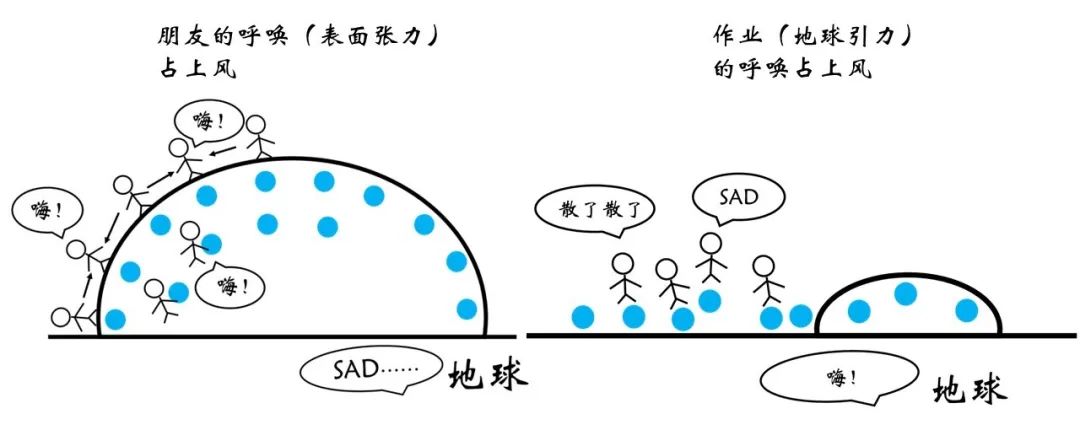
图13 重力与张力的竞争

不难想象，如果张力很强，液滴就会维持住近似球形的形状而不坍塌。如果张力很弱，无法与重力抗衡，液滴就会破碎。回到吹泡泡的问题，之所以一般要蘸肥皂水而非纯水，就是因为纯水的表面张力较小，不足以与液膜所受的重力抗衡。然而在太空中，重力不再作用，水膜便可以稳定存在了！

进一步地，就涉及到一个问题：不同物质的表面张力的大小与什么有关呢？在定性上，我们可以引入称为亲和度的概念，它反映了界面两侧物质亲疏关系。如果两侧的物质很亲和，那么待在内部和表面其实区别不大，毕竟大家都合得来，因此表面张力相对较小。反之，如果两侧的物质关系很疏远，表面张力会很大。而这，正是浸润现象产生的根源。

· Part 4：浸润，分子间的爱恨情仇 ·

浸润现象，这个词可能大家比较陌生，但是对应的物理现象非常常见。比如下图所示的防水衣服以及公交车车窗上的水滴就是非浸润和浸润代表性的场景。

图15 生活中的浸润与非浸润现象

仔细观察上面的场景，我们发现并不是只存在两种物质（准确的说应是物相，因为空气有复杂的成分），而是三种——一种作为基底的固体、一种液体和环境中的气体。因此，我们面对的浸润问题中所涉及到的界面也不是一种，而是两两之间组成的三种。

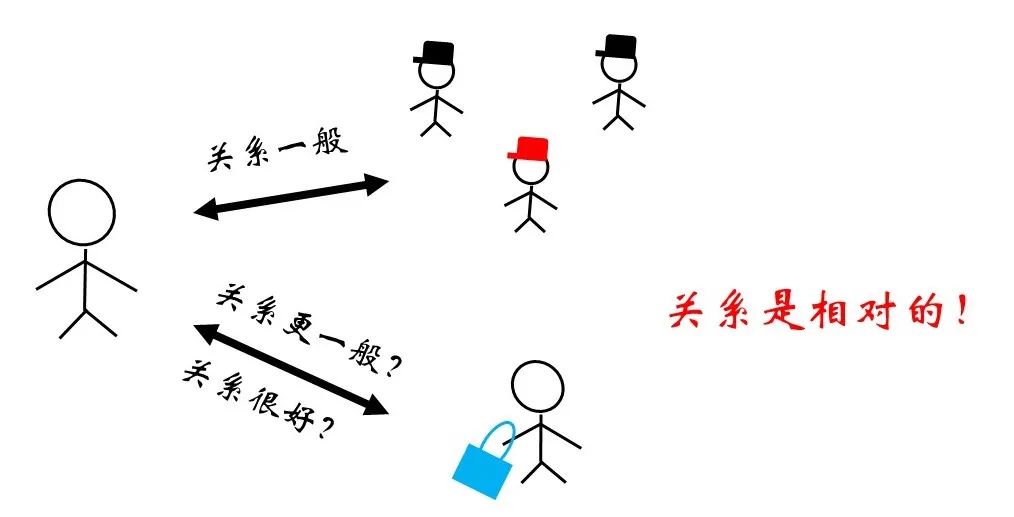
图16 物质间关系示意

很自然的，表面张力会存在于任何一个界面上，其大小与两侧物种的相对亲和关系有关，而方向沿着界面指向使得该界面收缩的方向。而最终的状态需要让这三个力的分量达到平衡。

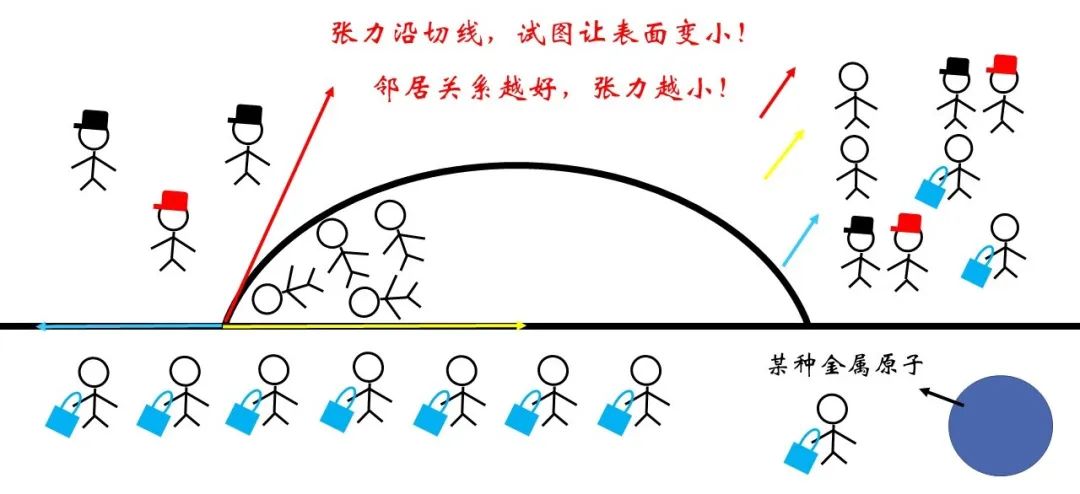
图17 三个界面交界处张力的竞争

对于浸润的情况，液体与固体物质间的关系很好，最为极端地可以认为该界面处的表面张力小到可以忽略。这样一来，需要红色和蓝色的力的水平分量达到平衡，液滴的形状趋于扁平。一般将气液界面处张力与液固界面的夹角称为接触角，对于浸润现象显著的亲水表面接触角很小。

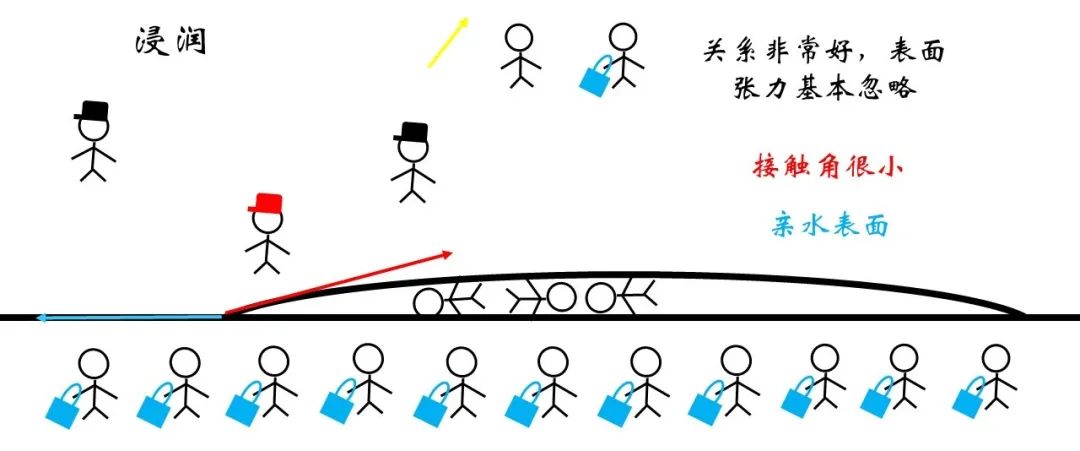
图18 浸润微观示意

反之，对于疏水表面，固液界面处的表面张力可能非常大，以至于接触角只有达到钝角甚至趋近于180°才能达到平衡，此时的现象称为非浸润或者不能浸润。而这种表面由于较高的疏水性被称为超疏水表面。

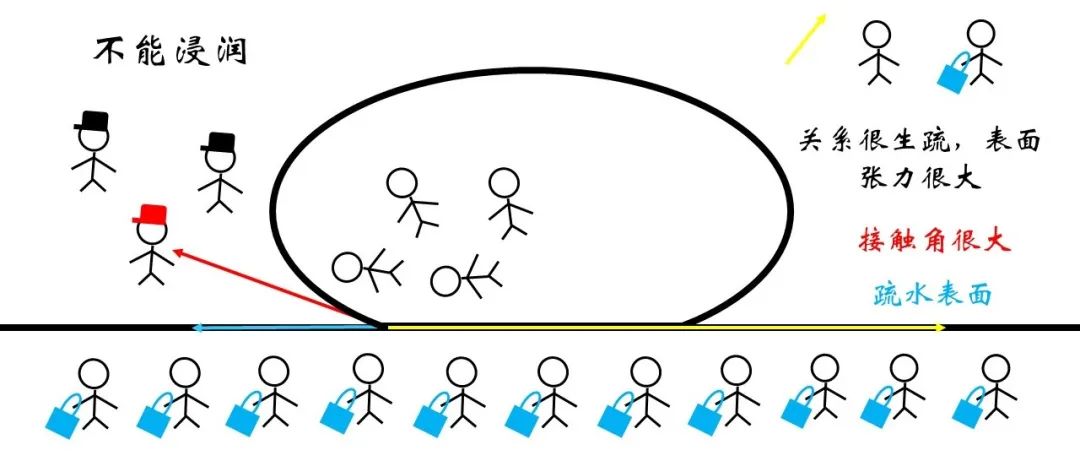
图19 非浸润微观示意

讲到这里，部分读者可能已经猜到了，荷叶的表面正是一种天然的超疏水物质，因此水在荷叶的表面呈现接近球形。

不仅是自然界中，科学家们在实验室中也制备出效果更加显著的超疏水或超亲水表面，比如下图中呈现出极端的非浸润与浸润现象。

图21 人工的超疏水/超亲水表面 | 图片源于【2】

审核编辑：刘清