理解信号的抽样与恢复过程

信号的抽样我们都知道了：

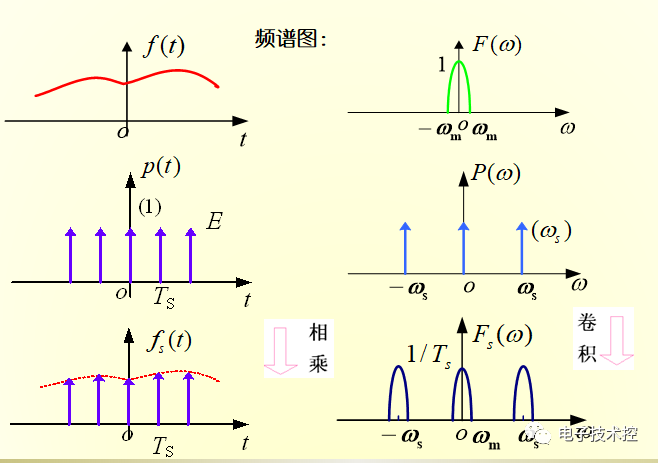
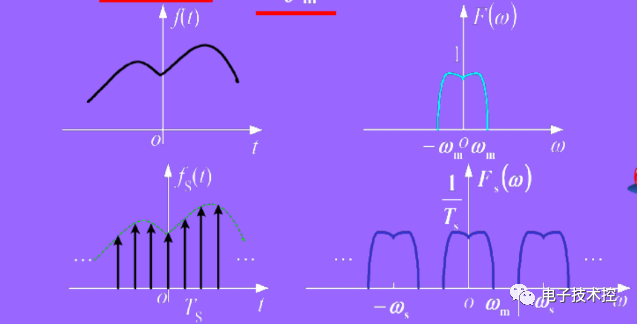
图1

上图最后一步冲激抽样信号的频谱的推导用到了这个公式：

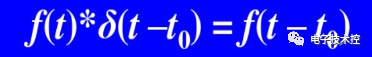
这个公式的推导可以参考：

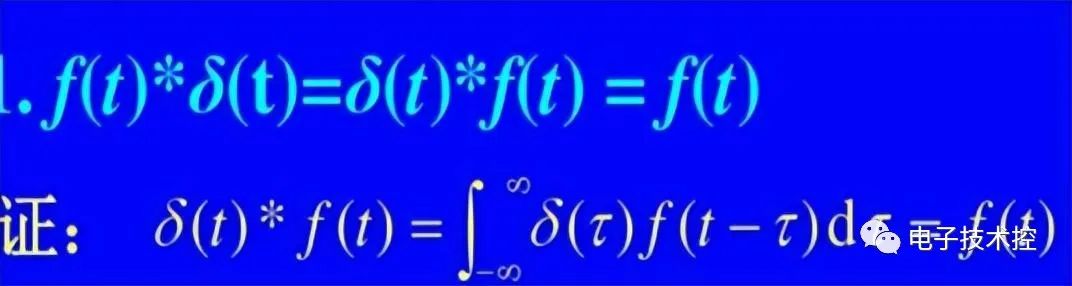
就是

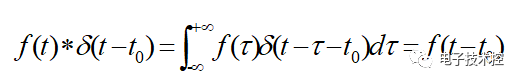
我们注意到图1中抽样函数的频谱

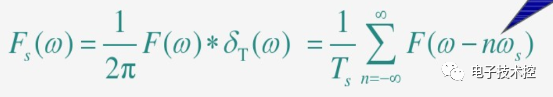
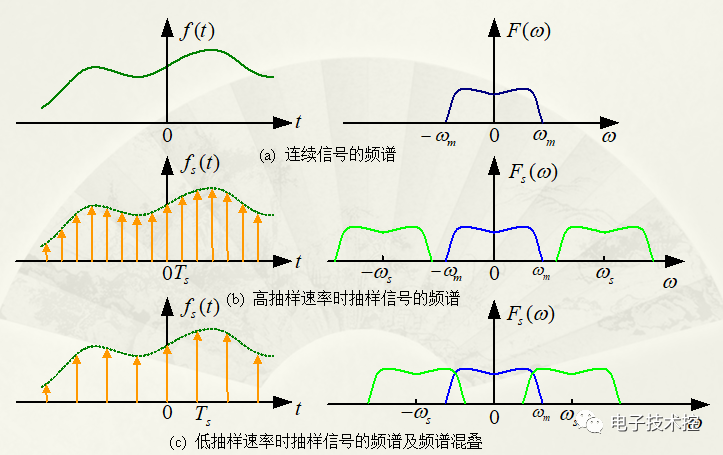
是由无穷个等间隔重复的频谱函数F(w)组成，这就是时域的离散导致的频域周期现象，如下图所示：

由于相同的频谱函数等间隔重复，就由可能导致频谱混叠现象，如下图：

为了能由频谱函数有效地恢复出原来的时域信号，就必须消除频谱混叠现象。在不存在频谱混叠的前提下，采用一个频域中的矩形滤波器H(w)将第一个周期的频谱函数取出，如下图：

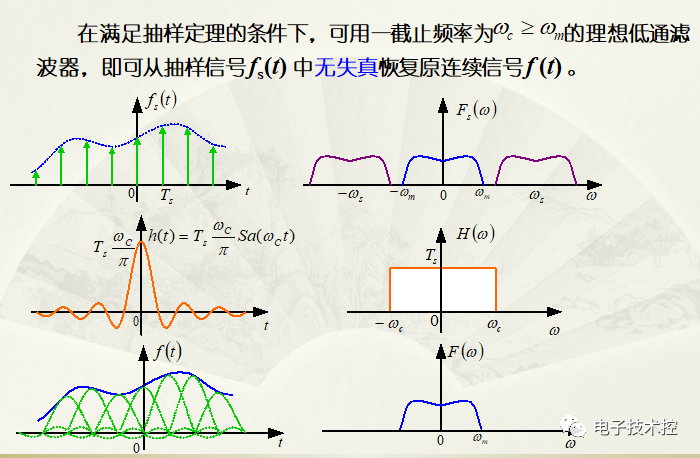
图2

由上图可以看到，频域中的矩形函数，在时域中是一个sinc函数。关于门函数，我们有：

对于单个门函数：

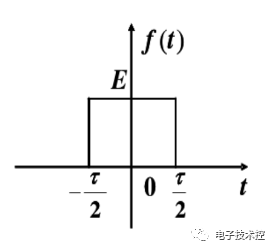
其频谱(傅里叶变换，积分限实际上是无穷)为：

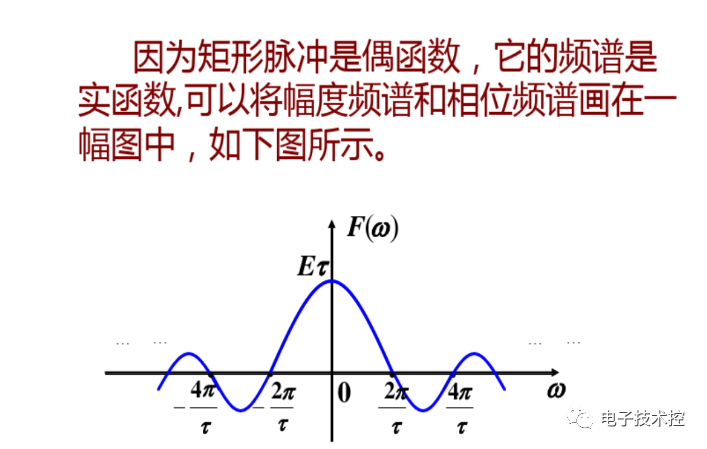
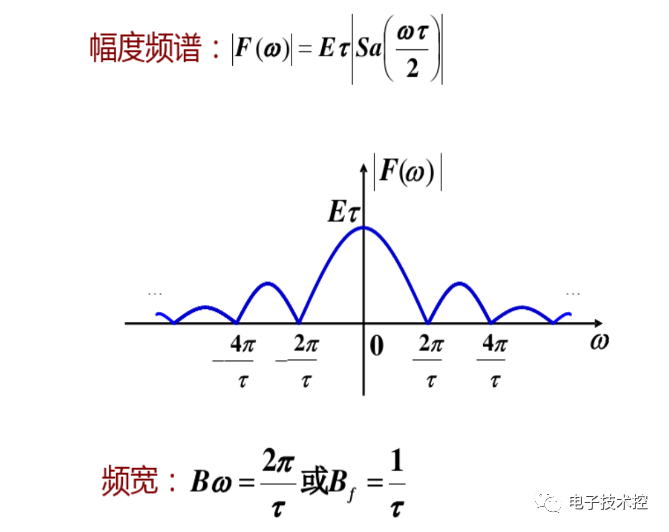
由以上分析看出，单个的门函数其频谱函数sa是连续的非周期函数，在w=0时取得最大值1。

下面通过图2中的低通滤波器H(w)进行信号恢复：

H(w)的时域函数为

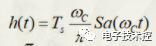
证明如下：

由于频域的乘积

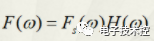
等于时域的卷积，得到：

上图表明，恢复出的时域信号f(t)是抽样点上的值f(nTs)与sinc(sa)函数在最大值点1(t=nTs)的乘积之和。

图解恢复过程：

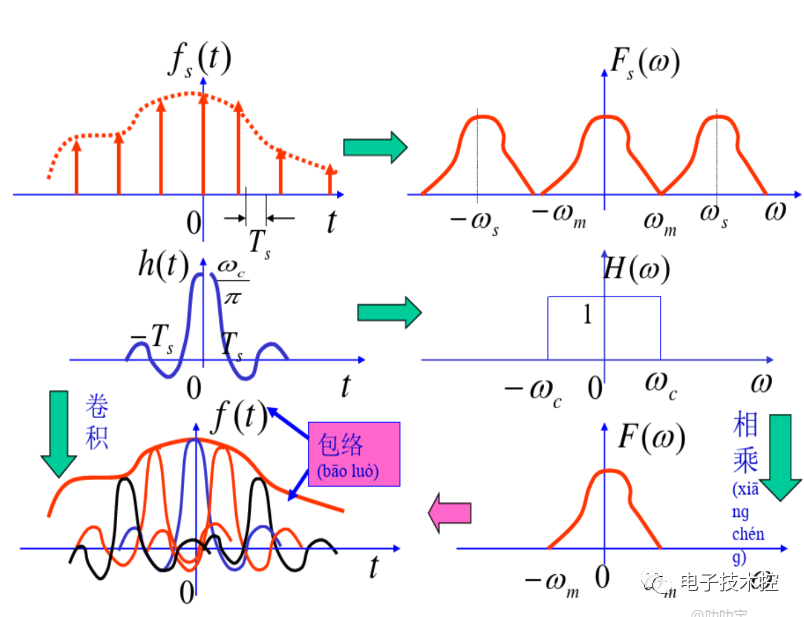
上图表明，最后恢复出的时域信号f(t)，是由一个个以nTS为中心点的sinc(sa)函数的最大值点构成的包络线。显然，TS越小，ws越大，恢复的效果越好。

也可以图解如下：

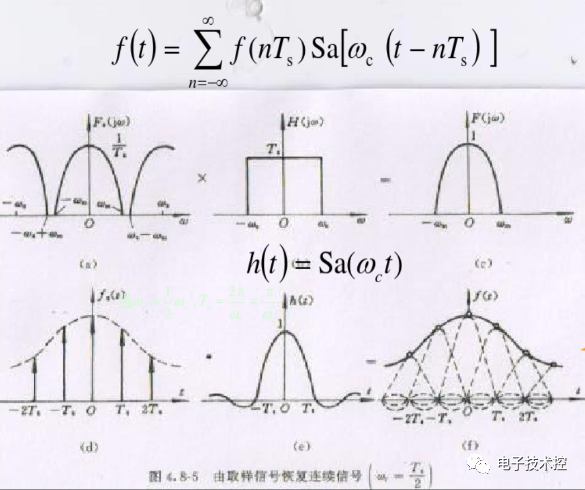
同样可以看出f(t)的构成过程。

简单总结：

1：时域信号抽样以后，得到按周期拓展的频域信号;

2：用一个频域的低通滤波器H(w)进行滤波，得到需要恢复的时域信号的频谱函数;

3：由于频域的乘积等于时域的卷积，得到待恢复信号与sinc(sa)函数的关系，从而确定f(t)是由一个个以nTS为中心点的sinc(sa)函数的最大值点构成的包络线，显然，TS越小，恢复的效果越好。

4：恢复出的时域信号f(t)实际上是由一个个sinc(sa)函数合成。

审核编辑：汤梓红