磁耦合电感器的基本定义

　　变压器是一种无源交流电路设备，它执行电压变换以升高或降低输入电压。

　　基本变压器方程

　　单个导电回路的法拉第定律是：

　　ε=−dϕdt，ε=−dϕdt， ［1］

　　其中 ε 是电动势或电压，dΦ/dt 是磁通量随时间的变化率。

　　多匝线圈相当于串联连接的各个回路，因此电压相加，法拉第定律变为：

　　ε=−Ndϕdt，ε=−Ndϕdt， ［2］

　　对于缠绕在同一个磁芯上且具有完美磁通耦合的两个独立线圈，dΦ/dt 很常见，因此

　　ε1=−N1dϕdt，和ε1=−N1dϕdt，和ε2=−N2dϕdt，因此ε2=−N2dϕdt，因此ε1ε2=N1N2，ε1ε2=N1N2，这表示电压比等于匝数比，这是变压器运行的基本定义方程。

　　场强和频率

　　以积分形式重写方程 ［1］ 给出：

　　Φ=−∫εdtΦ=−∫εdt ［3］

　　如果施加的电压是正弦时变的，则等式 ［3］ 可以写为

　　Φ=−∫ε0sin（ωt）dtΦ=−∫ε0sin（ωt）dt=ε0ωcos（ωt）=ε0ωcos（ωt）这表示通量与施加电压的频率成反比。通量是磁场 B 的法向分量在感兴趣的横截面上的积分。

　　Φ=∫BdAΦ=∫BdA如果 Φ 是正弦时变，幅度与频率成反比，则 B 也必须是正弦时变，幅度与频率成反比，可以写为：

　　B=B0ωcos（ωt）B=B0ωcos（ωt） ［4］

　　意义在于，随着操作频率的降低，磁场强度会增加。

　　BH循环

　　在铁磁材料中，材料中的总磁场是外加磁场和磁畴排列产生的内部磁场之和。材料中的总场表示为 B 并且在某些线性区域上可以近似为

　　B=μoμrH，B=μoμrH，其中 μ o是自由空间的磁导率， μ r 是材料的相对磁导率，假设为线性磁行为。图 1 显示了一个具有代表性的 BH 回路，它绘制了施加磁场循环时的磁场 B。在高磁场强度下，曲线变得非常非线性，并且据说材料已经达到磁饱和。随着接近磁饱和，H 的增加导致 B 值的增加要低得多。

　　

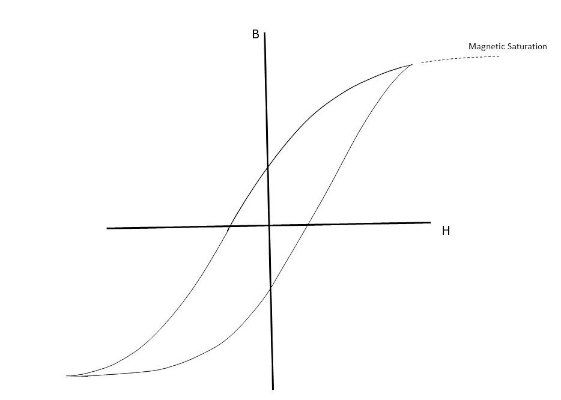
　　图 1. 铁磁材料的代表性 BH 回路。图片由 Blaine Geddes 提供

　　循环磁化材料消耗的能量是磁滞损耗，并作为 BH 回路的积分给出。BH 环的面积取决于材料的剩磁，它是重新排列磁畴所需的能量的函数。具有低剩磁的铁磁材料被称为软铁磁材料。硬铁磁材料具有更加开放的 BH 环，因为它们一旦磁化就会保持其磁性状态。对于在交流电路中的使用，显然更优选软铁磁材料。

　　当达到磁饱和时，不仅磁滞损耗达到最大值，而且电流的任何增加都会导致磁场强度的增加可以忽略不计，因此它只是被浪费为绕组中的 I 2 R 损耗。

　　从等式［4］可知，磁场随着施加频率的降低而升高，因此为避免磁饱和，变压器、电机等交流磁性设备的物理尺寸必须随着线路频率的降低而增大。

　　调整核心大小

　　硅电工钢的最大工作场强通常在 1.3 – 1.7 T 范围内，尽管一些晶粒取向合金钢可以支持更高的场强。M-6 电工钢（晶粒取向 3% Si）的饱和场强规定为 1.9 T。铁芯需要运行的越接近磁饱和，损耗越大，因此需要一定的余量。确定磁芯尺寸的第一步是选择磁芯中允许的最大工作磁场强度，这取决于为磁芯选择的电工钢等级。

　　对于给定的施加电压和匝数，多匝线圈的法拉第定律给出 dΦ/dt。积分 dΦ/dt 将给出总通量 Φ。对于正弦电路，Φ 将是正弦曲线，其幅度为 1/ω 因子。

　　应用 = BdA，允许确定给定核心区域的场 B，或给定指定的最大允许场 B 确定的区域。增加横截面积或增加匝数将降低最大场强，因此，这些是调整的主要变量，以在尺寸、成本和性能权衡方面提供可接受的设计。变压器尺寸与频率成反比，因此线路频率是一个重要参数。为 60 Hz 设计的变压器在 120 Hz 下可以正常工作，虽然它会过大，但如果在 30 Hz 下运行，它可能会变得非常低效和过热。

　　一旦基于上述权衡匝数和磁芯横截面积的考虑为初级绕组选择了匝数以实现可接受的最大场强 B，次级绕组的匝数简单地设置为所需的电压比。铁芯还需要足够的空间来容纳绕组线圈。线圈的线规将由所需的电流来设置，以将绕组中的电流密度保持在可接受的水平，从而最大限度地减少绕组中的 I 2 R 损耗。铁芯窗口区域必须足够大，以容纳随匝数缩放的绕组和基于最大电流的所需线规。

　　应用所有方程和权衡使变压器设计成为一个迭代过程，其中需要做出一些假设并重复计算。考虑到变压器的伏安额定值、最大允许 B 场、最低工作频率、铁芯几何参数以及可能的其他参数，如导线电阻率、允许导体损耗等，已经开发了各种公式来估计铁芯尺寸。所有这些公式都是基于法拉第定律和基本几何学的基本原理。

　　变压器是一种看似简单的无源器件，但设计它涉及操纵许多变量以产生适当优化的设计。

　　变压器结构

　　用于电源线频率和频率高达几千赫兹的变压器由交错的电工钢片构成，这些电工钢冲压成型以提供线圈的铁芯和绕组的窗口区域。叠层结构减少了涡流损耗。片材的表面涂有一层薄薄的高电阻率饰面。图 2 显示了一个典型的变压器，说明了它的叠片铁芯结构。各种核心几何形状很常见。这个绕组以相同的形式缠绕在一起。

　　变压器等效电路

　　图 3 显示了变压器的等效电路，其所有量均以初级侧为参考。来自次级侧的量以 1/N 2因数反射到初级，其中 N 是次级与初级匝数比。

　　

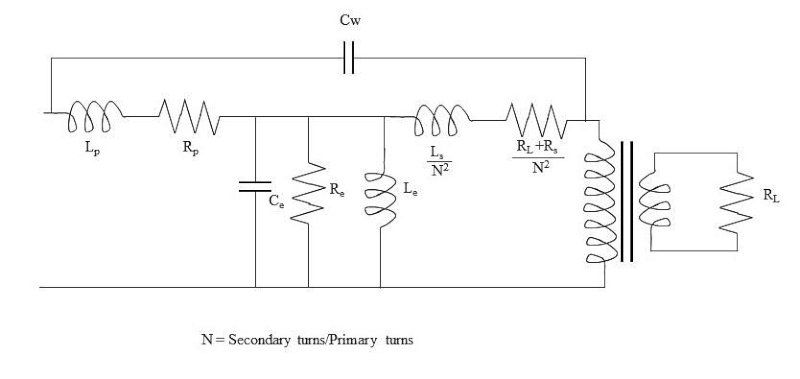
　　图 3. 所有量都参考初级侧的变压器等效电路。图片由 Blaine Geddes 提供

　　在等效电路模型中，R L 是负载电阻。R s 是次级绕组电阻。L s 是次级绕组电感。R p 和 L p 分别是初级绕组电阻和电感。Re 代表铁芯损耗，它由涡流损耗和磁滞损耗组成。L e 表示铁芯的循环磁化效应，其中涉及铁磁材料磁畴的移动，因此将其建模为电感器。

　　由紧密的绕组间距和绕组到外壳电容产生的寄生电容集中在一起作为一对电容器 C w和 C e，但它们很复杂，因为许多绕​​组会产生无数的寄生电容效应。幸运的是，这些电容效应很小，在低频时可以忽略不计。

　　高频变压器

　　由于 1/ω 对磁芯中磁通密度的影响，电感器和变压器的物理尺寸会随着工作频率的增加而缩小。

　　由于围绕 BH 回路的循环率增加，滞后损耗随频率增加而增加，因此，高频需要非常软的铁磁材料。涡流损耗与频率的平方成正比，因为根据法拉第定律，驱动涡流的感应电压与 dΦ/dt 成正比。

　　叠层电工钢芯变压器用于高达几千赫兹的频率。对于超过约 10 kHz 的频率，通常使用铁氧体。铁氧体是陶瓷。它们是金属氧化物的混合物，主要由铁、锰、锌和镍的氧化物组成。铁氧体的磁导率要低得多，但电阻率要高得多。感应涡流的大小与材料的电阻成反比，因此涡流 I 2R loss 将随着电阻率的增加而成比例地下降。　　

      审核编辑：彭静