深度解析MegEngine 4 bits量化开源实现

随着深度学习的发展，其应用场景也越发的广泛与多样。这些多样化的场景往往会对实际的部署提出更加“定制化”的限制。例如，自动驾驶汽车对人体识别的精度要求肯定比图像识别动物分类的精度要求更加严苛，因为二者的应用场景和错误预测带来的后果截然不同。这些“定制化”带来的差异，对于实际部署的模型在精度、速度、空间占用上有更具体的要求。在很多场景中由于部署的设备算力不强、内存较小，导致对于模型的速度和空间占用具有严格要求，而经过量化的模型具有速度快、空间占用小的特性，恰恰能满足这种需求。

因此量化模型被广泛使用在推理侧，量化也成为了一个重要且非常活跃的研究领域。近期，MegEngine 开源了 4 bits 的量化的相关内容，通过 MegEngine 4 bits 量化实现的 ResNet-50 模型在 ImageNet 数据集上的精度表现与 8 bits 量化模型相差无几，并且速度是 TensorRT-v7 8 bits ResNet-50 模型的推理速度的 1.3 倍。这次实践为 MegEngine 积累了 4 bits 量化的相关经验。同时，MegEngine 决定将 4 bits 量化的相关代码开源，为大家提供可参考的完整方案，推动在更低比特推理领域的探索与发展。

背景

深度学习领域的模型量化是将输入从连续或其他较大的值集约束到离散集的过程。量化具有以下两点优势：

在存储空间上，相较于 FLOAT 的 32 bits 的大小，量化值占用的空间更小。

在性能上，各类计算设备对量化值的计算能力要高于 FLOAT 的计算能力。

本文中提到的 n bits 量化，就是将 FP32 的数据约束到 n bits 表示的整型数据的过程。量化依据数据的映射特征可以分为线性量化和非线性量化，MegEngine 中采用的是线性量化，使用的量化公式和反量化公式如下：

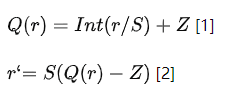
其中，Q 是量化方法，r 是真实获取的输入 FLOAT 值，S 是 FLOAT 类型的缩放因子，Z 是 INT 类型“零点”。

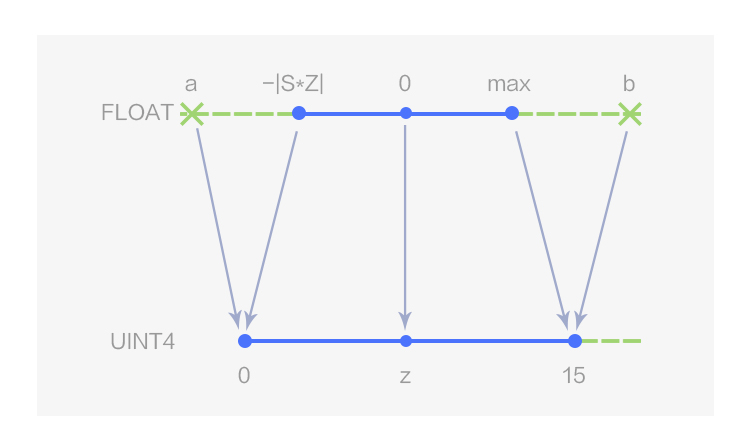
图1 4 bits 非对称线性量化

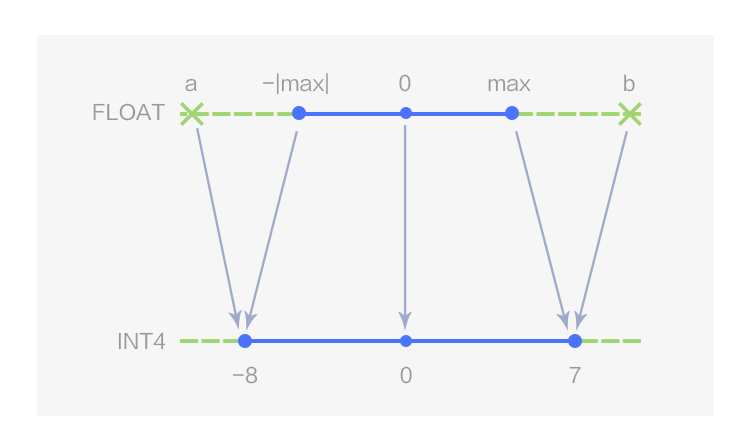
图2 4 bits 对称线性量化

如图 1 所示，MegEngine 用数据类型 UINT4 表示 4 bits 的非对称线性量化，量化值的取值范围为[0,15]；当 Z 取 0 时即为对称线性量化，此时 4bits 量化值的取值范围为[-8, 7]，在 MegEngine 中用数据类型 INT4 表示，如图 2 所示。

目前 8 bits 量化模型在一些场景下被业界广泛运用，我们想去了解 4 bits 量化模型的落地的可能性。这要解决两个问题：一方面，4 bits 量化模型的精度要如何保证；另一方面，4 bits 量化模型的速度能提升多少。要解答这两个问题，需要算法研究员和工程开发人员的通力协作进行验证。整件事情投入高，收益不明确。我们想找到开源代码，快速从原理层面对这两个问题有个判断，但经过调研发现目前并没有 4 bits 量化相关开源内容可供研究参考。所以，MegEngine 决定开发 4 bits 量化并解答这两方面的问题。

缓解精度下降

保证 4 bits 量化模型的精度是重中之重，如果模型精度无法满足需求，则 4 bits 量化的开发将毫无意义。为了避免精度的大幅下降，MegEngine 采取的举措是输入和输出采用非对称量化 UINT4，weights 采用对称量化 INT4，bias 采用 FP32。接下来，从计算公式的推演上，来看这样设计的合理性：

FP32 原始计算一次卷积输出结果的公式：

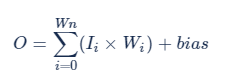
结合公式 [1]、[2] 推导的 4 bits 量化的公式：

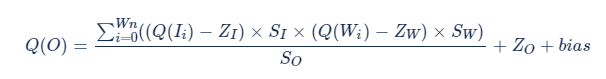
优化之后的公式：

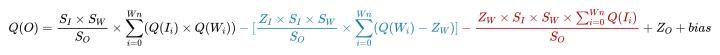
在上述公式中，ZI、ZW 是否等于 0，表明输入/输出和 weights 采用 INT4 还是 UINT4。并且在该公式中，除了Q(Ii) 的值需要推理时确定，其余值均可在推理前获得。所以，依据数据的计算特性，将这个公式分为了三个部分，分别用三种颜色表示：

黑色表示无论输入/输出以及 weights 数据类型如何选择，一定有的计算量。因为无法避免，所以不用考虑这部分的数据特性。

蓝色表示可以在推理前计算好的数据。

红色表示必须在推理时才能计算的数据。

推理前可以计算好的这部分数据可以提前计算并融合进 bias 中加入后续计算，所以 bias 必须用 FP32 数据类型表示，否则精度会大大降低。

至于输入/输出以及 weights 的数据类型选择，结合上述公式可以推导得出：

全用 INT4 时，即ZI、ZW 均等于 0， 计算量最小，只有黑色部分公式。

输入/输出用 UINT4，weights 用 INT4，即ZI 不等于 0，ZW 等于 0 时，会增加蓝色公式部分的计算量，但是这个部分是可以提前运算好的，对整体计算时间影响不大。

weights 用 UINT4，即ZW 不等于 0 时， 会增加红色公式部分的计算量，会对整体的计算时间带来较大影响。

由于 ResNet-50 模型 conv_relu 算子中的 relu 操作，输入/输出层的数据比较符合非对称的特性，采用非对称量化能更好地保留数据信息减少精度损失，所以输入/输出应该选择 UINT4，排除了上面三种方案中的第一种。第三种方案计算量会大很多，但是对精度的收益并不明显。所以，最终选择输入和输出采用非对称量化 UINT4，weights 采用对称量化INT4的方案。

缓解精度下降

提升模型性能并非一个简单的“因为计算设备的 4 bits 算力大于 8 bits 算力，所以易知......”的推导，计算设备 4 bits 算力大于 8 bits 算力是已知的，但是需要一些方法将这部分的算力“兑现”，算力需要合适的算子释放出来，其次，4 bits 量化所追求的也并非在某个算子的性能上超过 8 bits 量化，而是在模型层次超越 8 bits 量化。考虑到ResNet-50 模型以及卷积算子非常具有代表性，我们最终决定用 ResNet-50 模型作为基准测试模型。经过对模型的分析，发现 ResNet-50 模型的性能瓶颈主要集中在两个方面：

小算子比如 relu、add 较多，这些细琐算子带来的启动以及带宽上的开销较大。

conv 计算非常多，占用了全图 80% 以上的运算时间。

为解决这两方面的瓶颈，MegEngine 做了以下两个方面的优化工作：图层次的算子融合以及算子层次的优化。

算子融合优化

MegEngine 通过对计算图进行扫描匹配，并将匹配到的图结构替换为优化后的图结构。ResNet-50 模型所用的两种 pass 转换如下图所示:

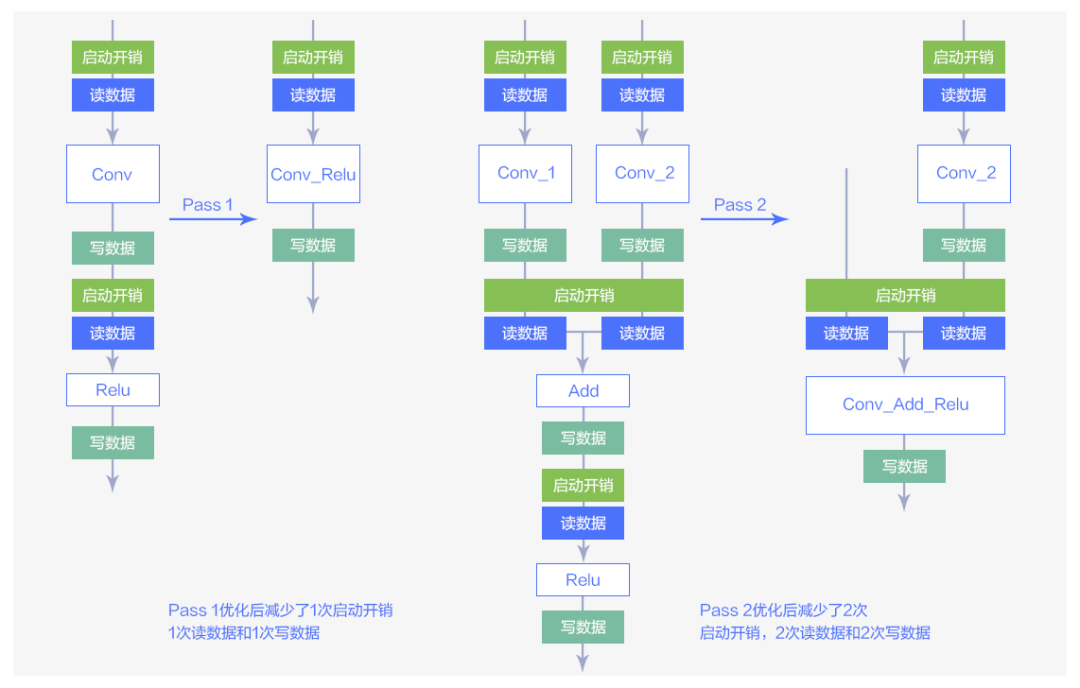
图3 两种Pass优化方法

图 3 中的大方块表示图中各种算子，小方块表示这些算子的读/写数据操作以及启动开销。从图中可以看到经过算子融合的优化可以有效减少算子的读/写数据的操作以及启动开销。

将这两个 pass 应用于原始的 ResNet-50 的结构，就可以得到优化后的图。

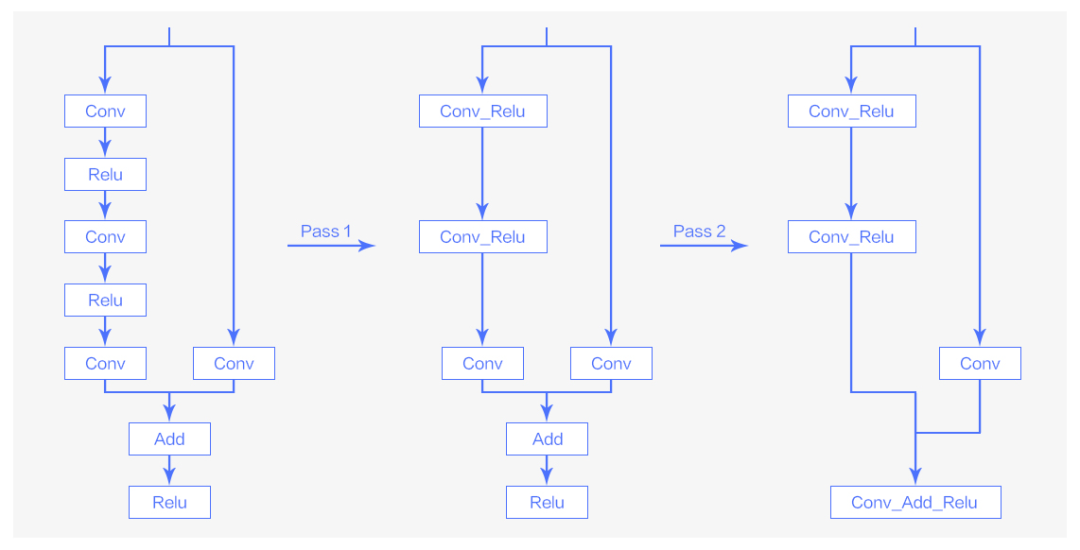
图4 Pass优化在ResNet-50模型中的应用

从图 4 可以看到，通过对 ResNet-50 模型的网络结构的优化，add 和 relu 这些计算强度较小的算子已经被 conv 这种计算强度大的算子所吸收，减少了小算子带来的启动以及读写上的开销。

conv 算子优化

经过算子融合优化后，可以看到 ResNet-50 模型调用的算子主要是各种 conv fuse 的算子，如 Conv_Relu、Conv_Add_Relu，这些算子的主体部分都是 conv，所以主要的优化也都落实在了 conv 算子优化上。

conv 采用 implicit gemm 算法并通过 mma 指令调度 tensor core 进行计算加速。顾名思义，implicit gemm就是将 conv 运算转换为矩阵乘的一种算法，是对 img2col 的算法的改进，传统的 img2col 算法如下：

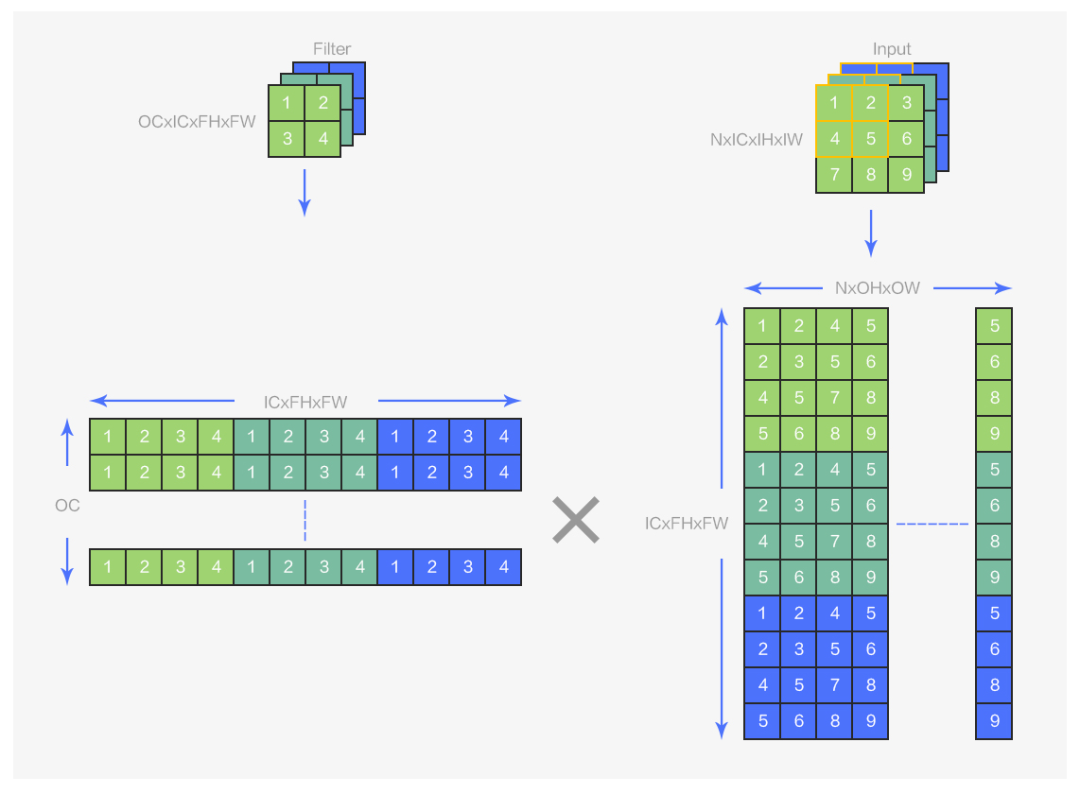
图5 img2col示意图

从图 5 中可以看到，img2col 是将输入 shape 为（N,IC,IH,IW），卷积核 shape 为（OC,IC,FH,FW）的卷积运算变为 shape 分别为（OC，ICFHFW）和（ICFHFW，NOHOW）的两个矩阵的乘法运算。implict geem 的整体运算逻辑与 img2col 相同，其区别在于 img2col 会“显式”地完成图 6 中数据的卷积排布到矩阵排布的转换，需要额外开辟一块矩阵大小的空间用以存储转换后的矩阵，implict gemm 的转换则是“隐式”的，没有这部分空间开销，在 implicit gemm 算法中并没有开辟额外的空间存储卷积核矩阵（OCxICFHFW）和输入矩阵（ICFHFWxNOHOW），而是在分块后，每个 block 会按照上图中的对应逻辑，在 global memory 到 shared memory 的加载过程中完成从数据的原始卷积排布到 block 所需的矩阵分块排布的转换。

针对 4 bits 的 implict gemm 的优化主要参照 cutlass 的优化方案，并在此基础上加入了 output 重排的优化。由于篇幅问题，本节仅讲解 output 重排的优化，想要了解更多技术细节，建议参考阅读之前的文章以及开源代码。

先分析 output 目前的排布情况，implict geem 的计算最终都落实在了 mma 指令上，而 mma 指令输出的排布与 warp 中 32 个线程的关系如下：

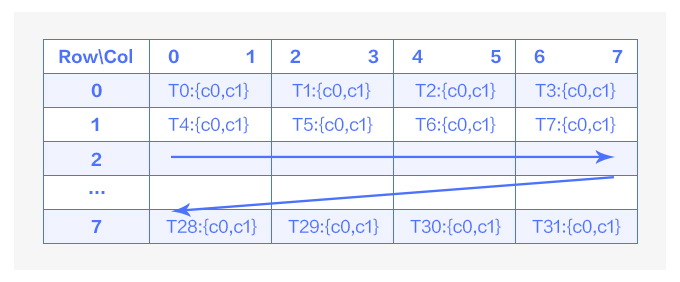
图6 mma输出排布示意图

如图 6 中所示，在一次 mma 指令运算中，一个 warp 的 32 个线程负责 64 个运算结果，且这些结果都存储在寄存器上。每个线程负责 8x8 的结果矩阵同一行内连续的两个运算结果，每四个线程负责同一行的 8 个运算结果。

结合 implict geem 的结果矩阵 OCxNOHOW（由 OCxICFHFW 和 ICFHFWxNOHOW 乘积得到），在MegEngine 4 bits 量化的卷积算子设计中，一个 warp 的 32 个线程和输出的排布关系如下：

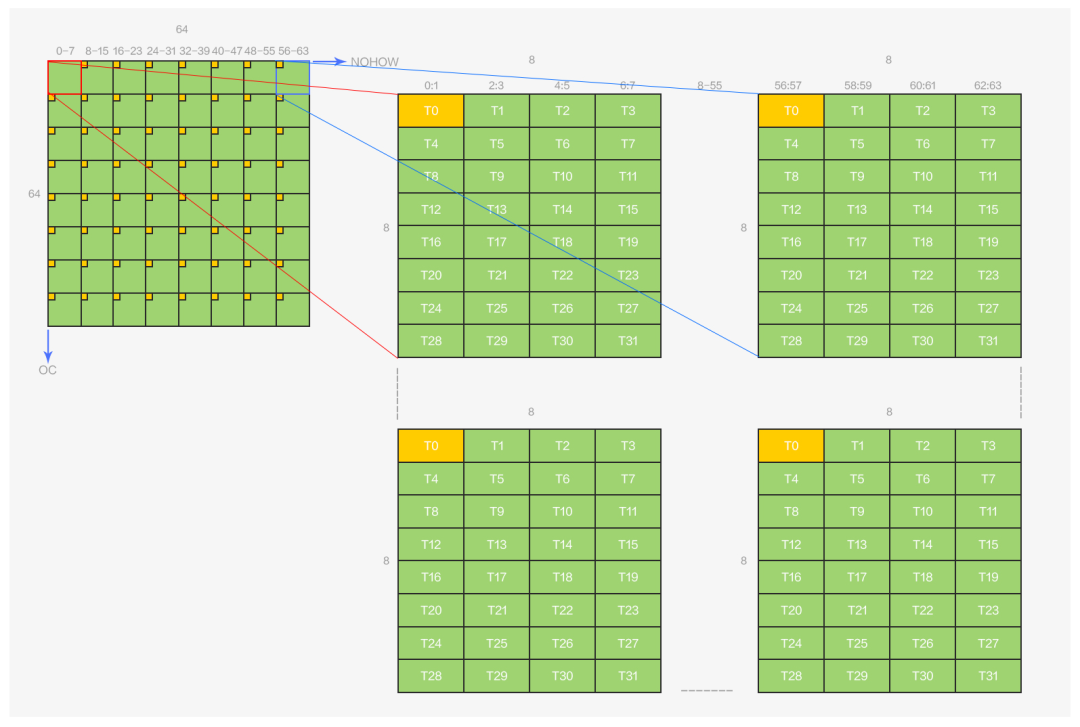
图7 warp输出排布示意图

一个 warp 负责 64x64 大小的输出矩阵，该矩阵由 8x8 个 mma 的 8x8 输出矩阵组成，输出和线程的排布关系如图所示，黄色部分表示线程 0 所拥有的数据。图 7 中的所有数据都在寄存器上，算子的最后一步操作，也就是将这些数据写回到 global memory 上并按照 NCHW64 的方式进行排布。

一眼看上去，这些数据的排布都是间隔开的，虽然横坐标上的数据连续，但对于写回到 global memory 并按照 NCHW64 排布而言，并没有什么帮助。直接的写回方式是将这些寄存器上的数据进行压缩，先将 8 个32 bits的数据转换为 8 个4 bits 的数据，再将这 8 个 4 bits 的数据放到一个 32 bits 大小的空间，然后写回到 global memory，这种处理方式将面临几个问题：

每个线程中的数据都不连续，增大了数据处理难度，这些额外的处理计算可能会导致性能下降。

需要在纵向的 8 个线程间交换数据，会有同步的开销。

这无疑是一个开销比较大的处理方式，为了解决写回数据带来的性能问题，MegEngine 采用了以下处理方式：

注意到 NCHW64 的排布方式，每 64 个 OC 是连续的，尝试将矩阵旋转一下，想象这是一个 NOHOWxOC 的矩阵，那么 T0、T1、T2、T3 四个线程所负责的数据在 OC 维度上是连续的，它们对于的 OC 维度分别是

T0{0,1; 8,9;16,17;24,25;32,33;40,41;48,49;56,57}、

T1{2,3;10,11;18,19;26,27;34,35;42,43;50,51;58,59}......

可以看到，现在是四个线程负责 64 个连续的输出，那么只要这四个线程交换数据再压缩、写回即可。相比于之前 8 个线程间数据交换和写回，现在的处理方式更加简单，内部偏移计算与同步开销会更少。所以实现output转置是一种切实可行的优化方法。这也体现了 NCHW64 的排布方式使得 4 bits 类型的数据在传输过程能被连续访存，充分利用硬件资源的特点。

但是线程间交换数据的开销在output转置处理中依然没有被彻底解决。如果可以得到

T0{0,1;2,3;4,5;6,7;8,9;10,11;12,13;14,15}、

T1{16,17;18,19;20,21;22,23;24,25;26,27;28,29;30,31}......

这样的输出OC 维度和线程对应关系。那么就只需要在线程内部进行数据打包和写回，并且 16 个4 bits 的数据正好占用 2 个32 bits 大小的空间，非常规整。要实现这个效果也是非常简单的：对于 AxB=C 的矩阵乘法，要实现 C 矩阵的列顺序变换，只需要对 B 矩阵进行对应的列顺序变换即可，如下图所示：

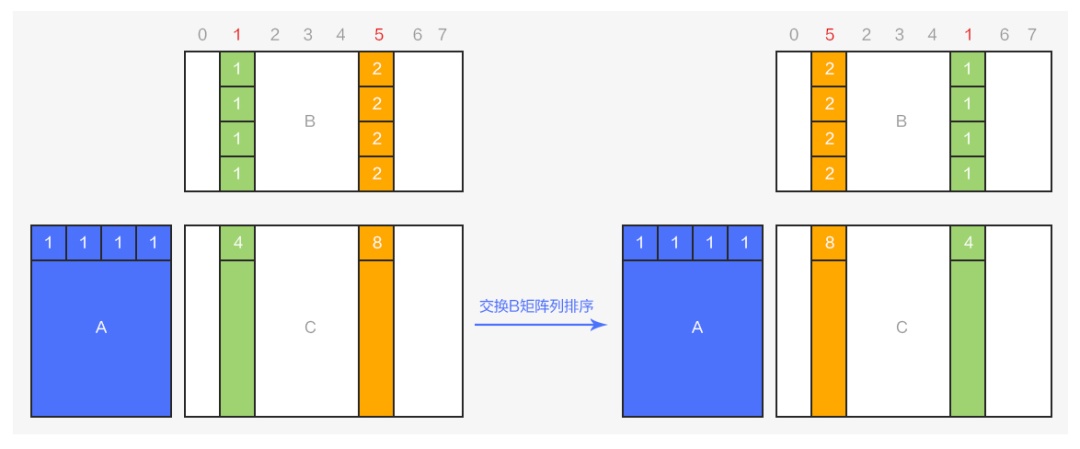
图8 矩阵乘积的列变换

从图 可以看出，将乘积矩阵 AxB=C 中的 B 矩阵的第1列和第5列进行对调，结果矩阵 C 对应的列的运算结果也会发生同步的对调。利用这一特点，可以在 conv 算子运算前，将 weights 的列进行重排序，使得最终输出OC 维度在对应的相同线程中保持连续，T0{0,1;2,3;4,5;6,7;8,9;10,11;12,13;14,15}...

所以总结一下 output 重排的策略，其实就两点：

将 OCxICFHFW 和 ICFHFWxNOHOW 的矩阵乘，变为 NOHOWxICFHFW 和 ICFHFWxOC 的矩阵乘，实现output 结果的转置，确保在 OC 维度上的数据连续，配合 NCHW64 的排布方式，便于将数据从寄存器上写回到 global memory 上。

通过对 ICFHFWxOC 矩阵的 OC 进行重新排序，实现 output 矩阵 NOHOWxOC 的 OC 维度和线程的对应关系更加合理，确保线程内部的数据连续性，避免线程间数据交换的开销。

总结 & 展望

本次开源提供了和 TensorRT(TRT) ResNet-50 8 bits 量化模型在 ImageNet 数据集上速度以及精度对比结果：

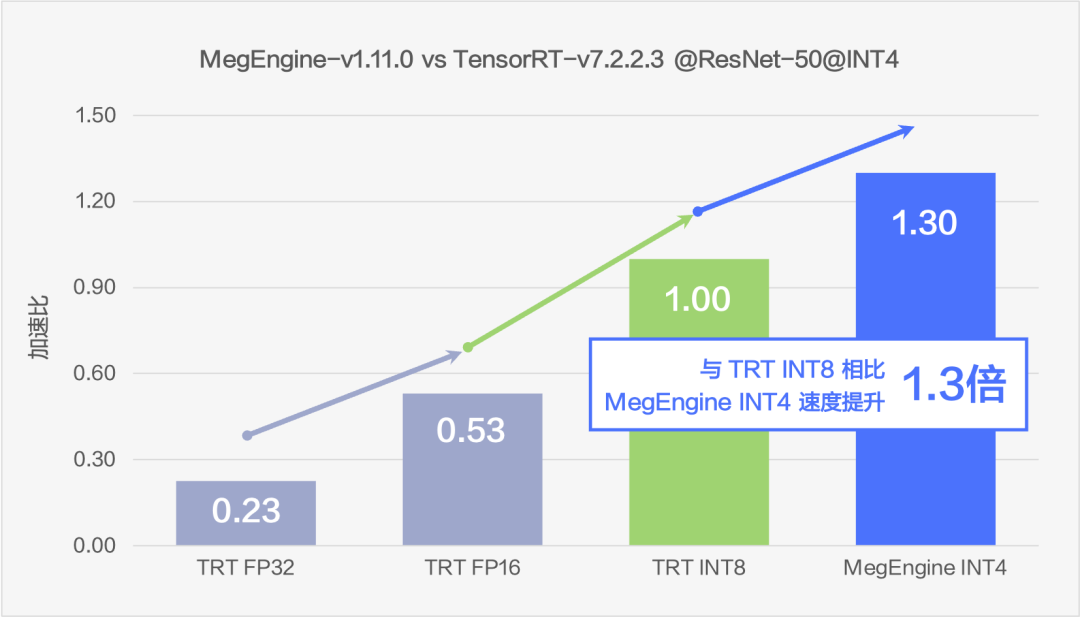
图9 速度对比

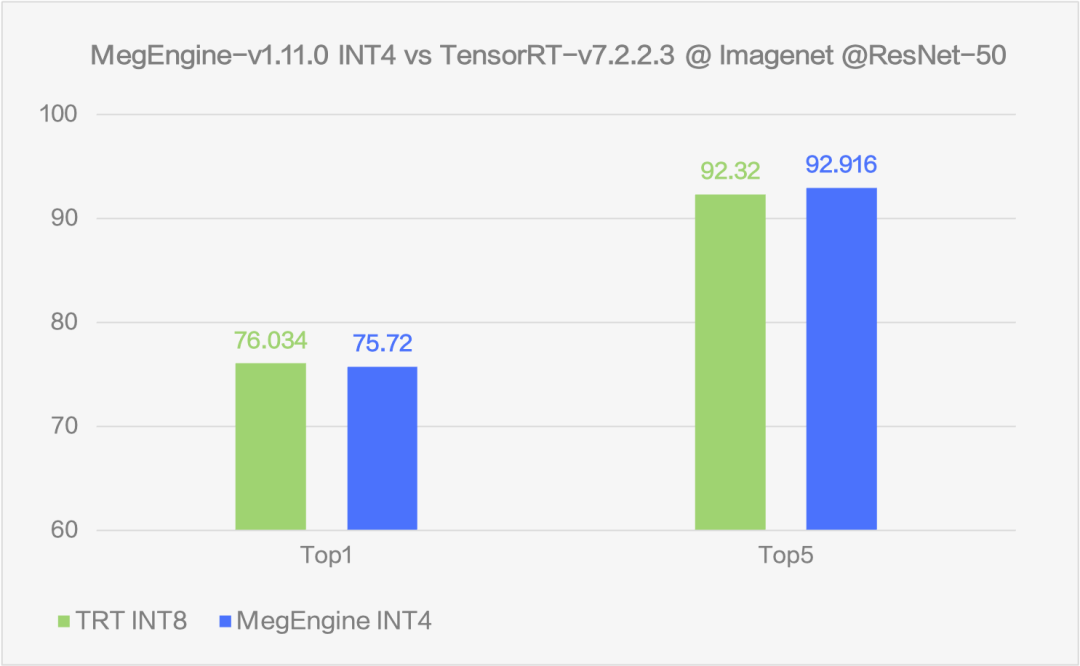
图10 精度对比

通过在 ResNet50 上的测试可以看到，MegEngine 的 INT4 方案可以比 fp32 推理速度提升 5.65 倍至多，相比于现在业内较为常用的 INT8 方案也仍然可以提升 1.3 倍的速度。在速度大幅提升的同时，uint4*int4 的方案尽可能的保证了精度，精度下降能够控制在 top1 -0.3% 左右。

在速度和精度两方面的努力，让 INT4 的方案能够在实际的业务场景中带来显著的优势，而不只是停留在论文上。

审核编辑 ：李倩