阻抗在交流系统中的作用

上一篇我们介绍了「阻抗」在直流电系统中的定义，也谈了「电阻」以及它在直流电路中的效应。

在交流甚至高频的系统，阻抗不只是电阻，它还有电容与电感的特性，因此在交流系统中的阻抗要用数学中的复数系统来标示。同样的，交流系统中的电压与电流在电容与电感存在时，也会产生相位上的差异，因此交流系统中的电压与电流也需要用复数系统来表示与计算。

这一回我们要来探讨一下「阻抗」在交流系统中的作用。

先从简单的开始

我们先从电阻开始，看一个简单的电路。

上一回我们用的 power source 是一个直流电压源，这一次我们要使用交流电源。假设有一个峰值电压 10 V、频率 100 Hz 的交流电源，我们将它接上一个 10 ohm 的电阻当作负载。这个电路就会长这样：

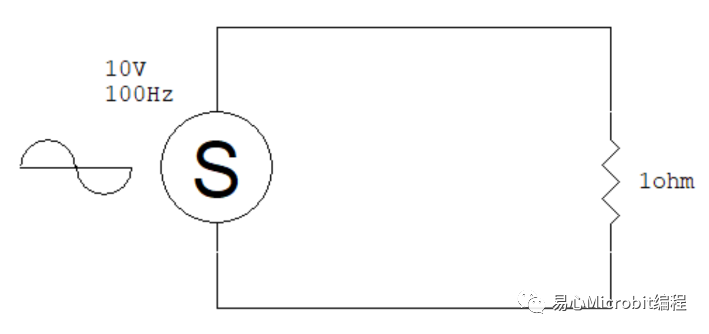
所谓的「100 Hz」交流电源，指的一定是 100 Hz 的正弦波，而不是方波、三角波、阶梯波或是任何其它的波形。傅立叶分析告诉我们，任何形状的周期波都可以用不同频率的正弦波迭加而成，因此当我们在探讨单一频率的波形时，讲的一定是正弦波。

这个交流电压源的电压波形就会长这样：

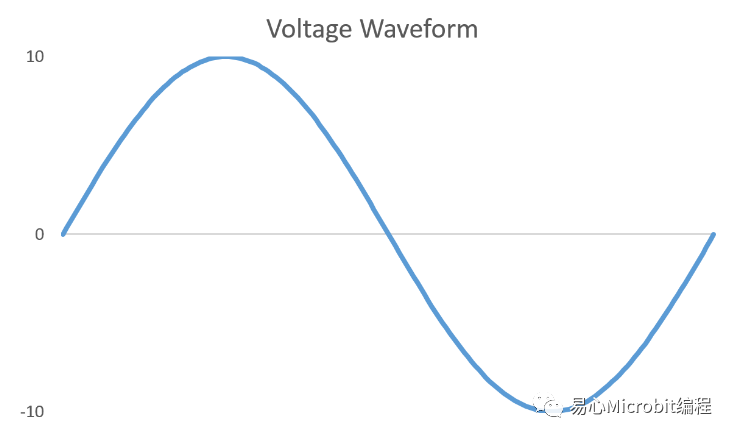
那么电流呢？我们上一次讨论过，如果电源是个电压源，要流出多少电流是由负载的电阻大小决定的，而对于一个会变动的电压源来说，即使它输出的电压在变动，它也时时刻刻遵守这个定律，也就是我们熟知的奥姆定律：V = IR。

当电压为 0 时，我们将电压（0 V）和负载（1 ohm）带入上式，就会知道电流也是 0；当电压上升到 5 V 时，我们将电压（5 V）和负载（1 ohm）带入上式，可以得知电流是 5 A；当电压上升到顶点 10 V 时，我们将电压（10 V）和负载（1 ohm）带入上式，就可以得知电流是 10 A。

然后有趣的事来了。由于这个电源是交流电，它的电压在整个周期中有一半的时间会低于 0，因此当我们把小于 0 的电压带入上面的式子计算时，电流也会小于 0；当电压是 -5 V 时，电流是 -5 A；当电压是 -10 V 时，电流是 -10 A。

电流的符号代表它流动的方向，如果我们定义电流由上往下流动是正的，那么当电压变为负的时候，电流就会由下往上流动。

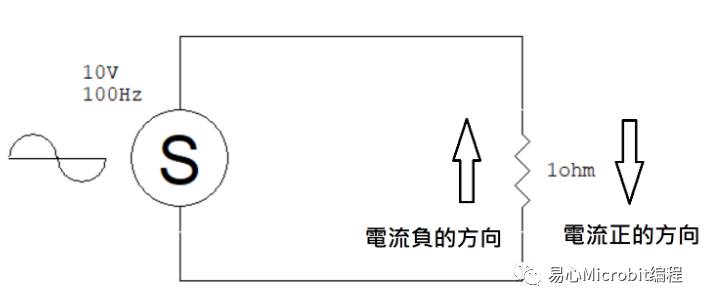
如果我们把电流波形画出来，就会是看起来就会是这样：

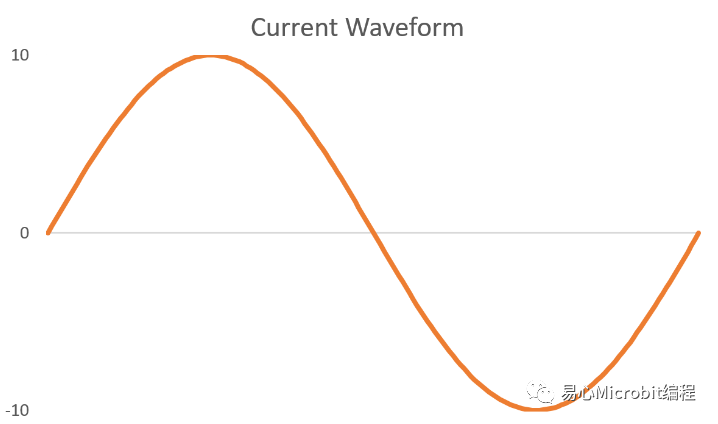
如果我们把电压波形和电流波形的时间轴对齐画在一起，看起来就会是这样：

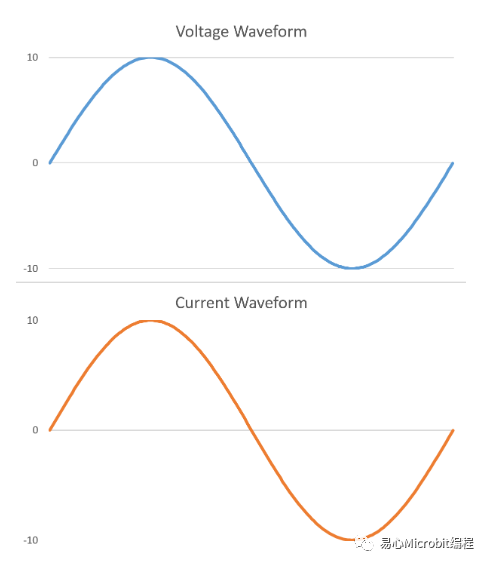
电流波形会随着电压的变化从 0 开始上升到最高点，再下降回到 0，然后变成负的，再到最低点，最后回到 0，如此周而复始。

由于电流波形很精确地随着电压波形变化，同时出发、同时达到最高点、同时达到最低点，因此我们说在这个电路中，电压波形与电流波形的相位相同。

电容器负载

如果我们将上面电路中的负载电阻换成一个 1 uF 的电容器，会发生什么事呢？这时电路会变成这样：

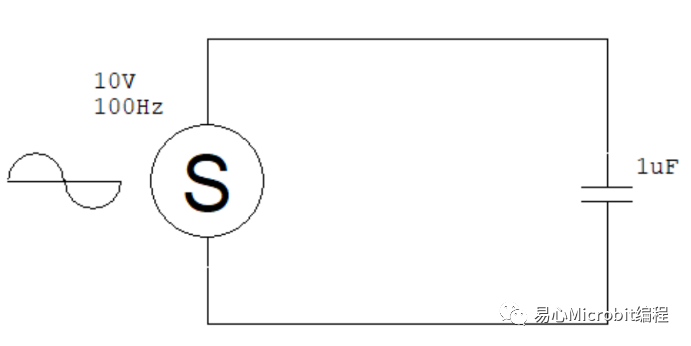
再次强调，由于电源是个电压源，电压波形由它自己决定，而电流波形则由负载决定，也就是说，电压是因，电流是果。

如果我们测量这个电路的电流波形，它会是这样：

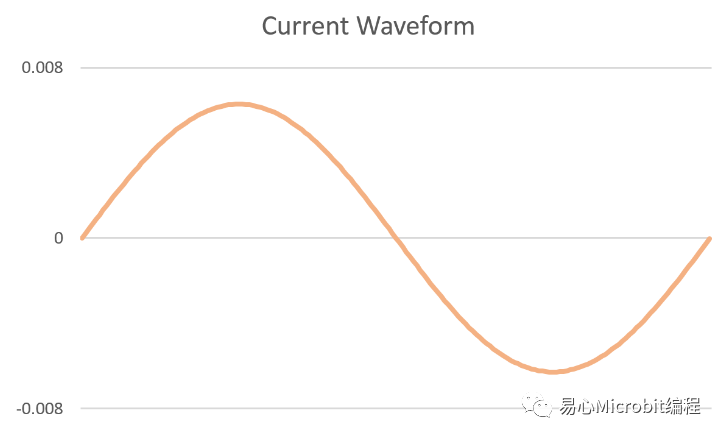
看起来仍然是个正弦波，没什么特别的，除了垂直刻度稍微怪了一点，但如果我们同时将电压波形和电流波形画在同一个时间轴上的话，就会是这样：

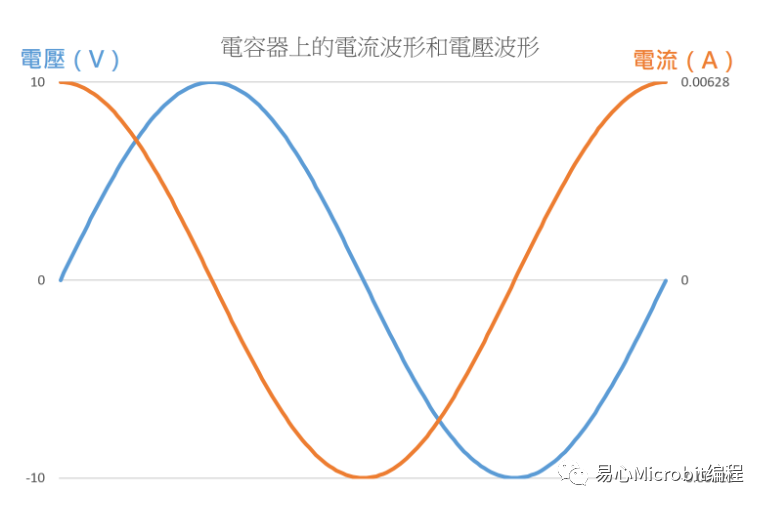
原来在交流电路中，电容器上的的电流和电压会有时间差。从这个图中看起来，电容器上的电流会比电压先上升到最大值，因此我们说电容器上的电流相位「超前」电压，或是电压相位「落后」电流。

至于超前或落后多少，其实可以很容易从图中看出来，刚好就是四分之一个正弦波的周期。如果用角度来计算，一个周期是 360 度，四分之一个周期就是 90 度。因此我们可以这样说：在交流电路中，电流相位超前电压相位 90 度。

相位差知道之后，我们再来看振幅。眼尖的读者可能已经看到，我虽然把电压和电流画得一样高，但其实它们的坐标轴不一样。电压的顶点依旧是 10 V，但电流的顶点只有 0.00628 A。这个 0.00628 A 是怎么来的呢？

电容有个公式叫做它的容抗，我们在以前的文章中偶尔会用到它：XC = 1 / 2。

　

      审核编辑：彭静