当均值不等式遇上高等数学会怎样

如果说高中有什么难度比较大的内容，那不等式绝对算是其中一大类，甚至在考试中往往作为压轴题出现。

说到均值不等式，还得从我们初中就熟悉的完全平方公式以及任意实数的平方大于等于0开始。  

假设x1和x2都是正实数，那么就有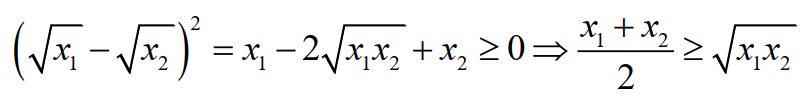  


 

利用上述关系，可以进一步得到

 
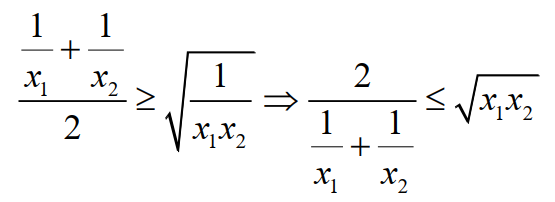
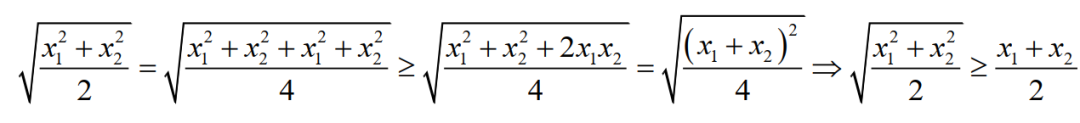
把上面所有内容整理一下，就有了我们高中非常熟悉（吗？）的均值不等式。


 

 
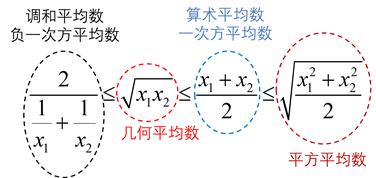
当然，上述结果也可以推广到n个正实数，即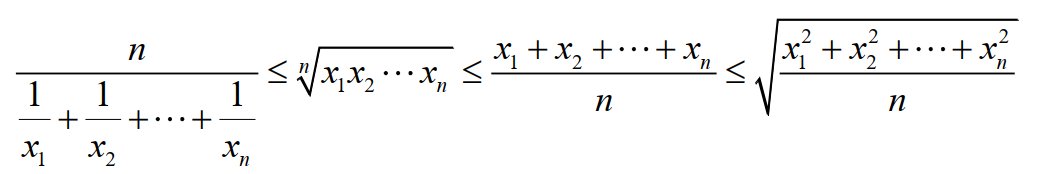  

n个正实数构成的均值不等式同样可以采用完全平方公式来证明（虽然有点麻烦），有兴趣的朋友可以试试。  

可是，作为一名学习过高等数学课程的博士研究生，能否对均值不等式进行深入探讨呢？

这里定义这样一个函数：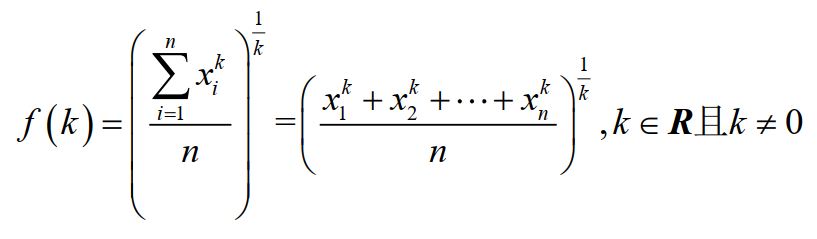  


                          

其中R表示所有实数的集合。   细心的朋友可以发现，f(-1)就是调和平均数，f(1)就是算术平均数，f(2)就是平方平均数。  

只要研究清楚f(k)的单调性，均值不等式问题也就迎刃而解了。

值得一提的是，几何平均数并没有包含在函数f(k)中，暂且不管它。

为了简化问题，首先只考虑两个数，即n=2的情况。

   

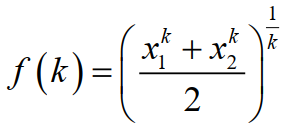
假设x1=1，x2=2。采用Matlab或Excel软件作出f(k)随k（-100≤k≤100且k≠0）的变化曲线。

 

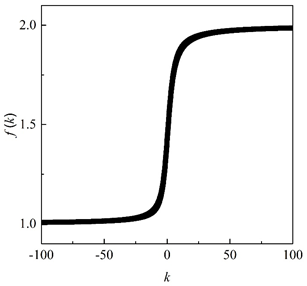
可以发现：

        将f(k)表达式整理一下，有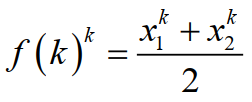  

也就是说，f(k)的k次方其实就是x1的k次方和x2的k次方之和的平均值，这也是为什么把f(k)叫作平均数的原因。  

事实上，f(k)是k的单调递增函数这一结论对于3个甚至n个数也是成立的。感兴趣的朋友可以尝试一下。    

学过高等数学的都知道，想要证明f(k)是k的单调递增函数，只需证明其导数大于等于0就行。  

这里重新写一下f(k)表达式
 

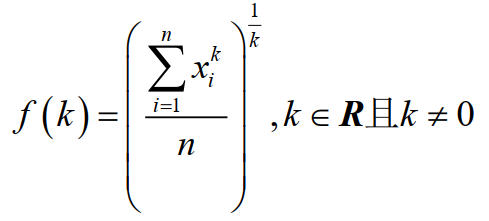
两边取对数求导后得到
 

 

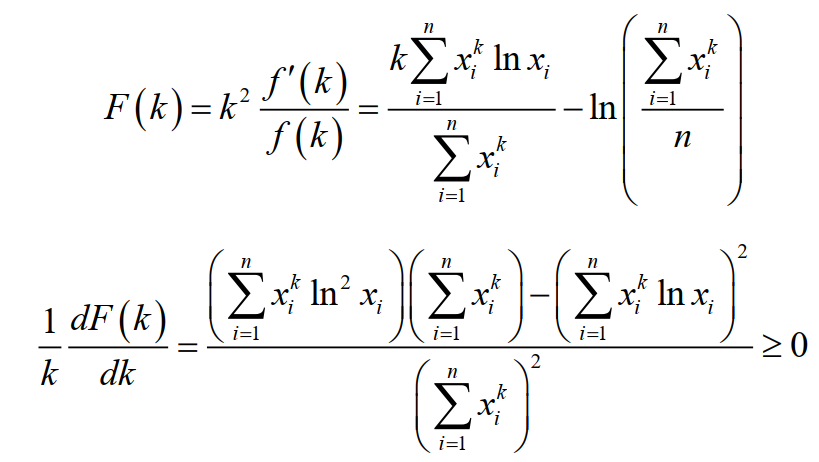
可见F(k)的导数与k同号，F(k)在k<0时为减函数，在k>0时为增函数，F(k)在k=0处有极小值。


   

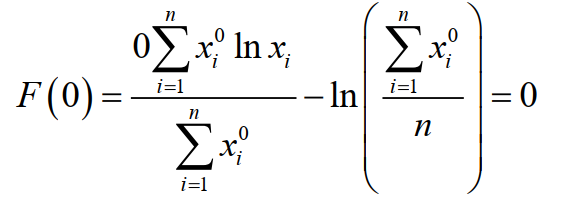
因此f(k)导数大于等于0，f(k)为单调递增函数。

 f(k)最小值和最大值分别在负无穷和正无穷处取得。  

利用夹逼原理求极限之后可以发现

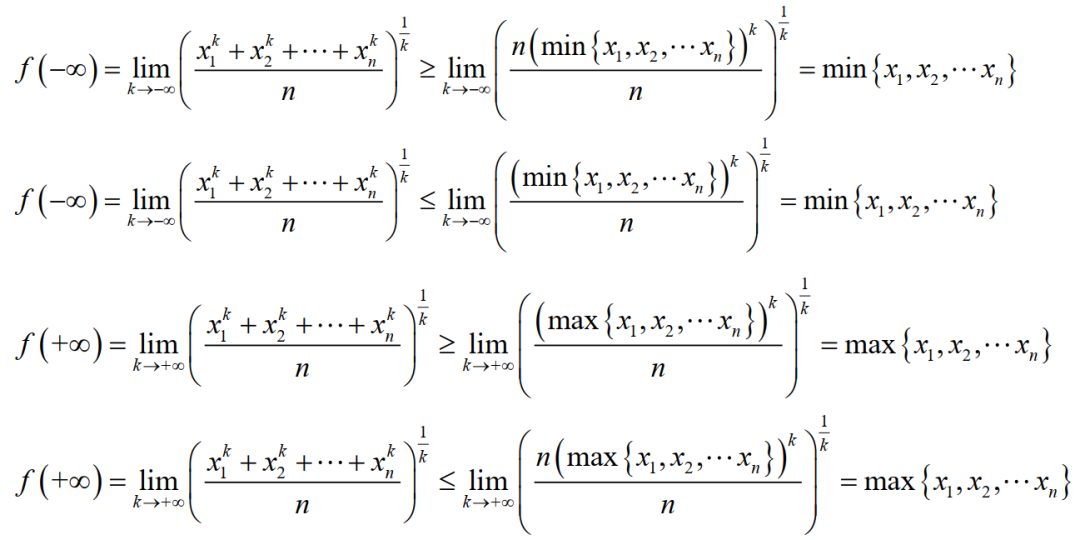
也就是  
 

 
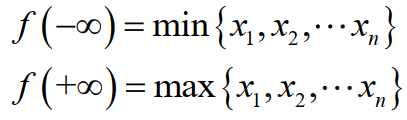
还有，我们应该注意到f(k)的定义域是不包含k=0这个点的，否则指数就会出现1/0这样的尴尬局面，但是我们可以求k趋于0时f(k)的极限。
 

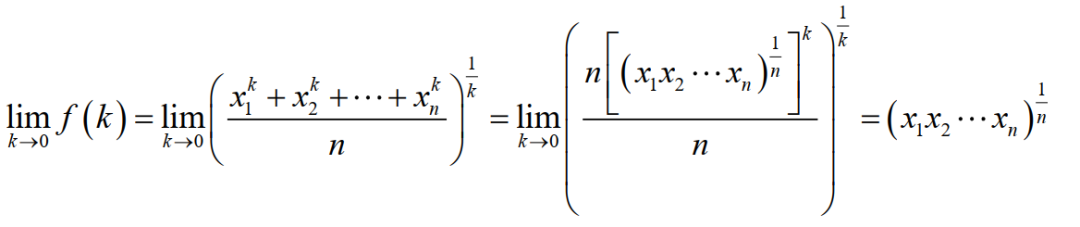
这不就是之前无法包含在f(k)定义中的几何平均数吗，居然出现在了这里。  

因此，可以定义f(k)最终表达式为

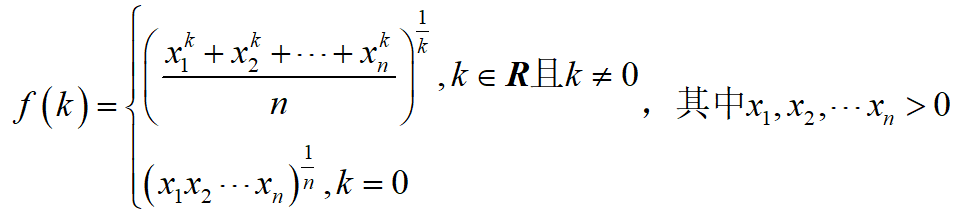
f(k)满足以下性质：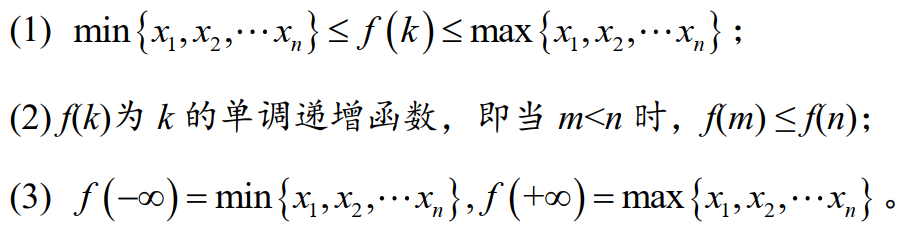  

此时，高中学过的均值不等式就可以表示为
 

 

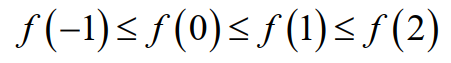
即 负一次方平均数≤零次方平均数 ≤一次方平均数≤平方平均数   可见其只是f(k)极为特殊的情况而已。

以上内容是小编怀着对数学的一腔热忱和好奇总结出来的，本以为能发个SCI论文，结果网络搜索之后发现，前人早就得到了上述结论，还将其称之为“幂平均不等式”（百度百科就有），小编的SCI梦想就此破灭。      





审核编辑：刘清