基于FPGA实现的自定义浮点数

1. 概述

基于FPGA实现各种设计的首要前提是理解并掌握数字的表示方法，计算机中的数字表示方法有两种：定点数表示法和浮点数表示方法。其中，对于浮点数尽管当前应用最为广泛的是基于IEEE 754所设计的浮点数表示方法，Xilinx（忘记Altera中是否有对应的IP核）的IP核中也提供了相应的设计方法，但其表示方法缺乏FPGA设计应有的灵活性，而且资源消耗相对严重，因此可以根据应用的需要，设计好基于FPGA实现的自定义浮点数。

2. 定点数表示

定点数大类上可分为有符号数和无符号数，需要清楚的是，无论是计算机还是FPGA，其底层并没有无符号数、有符号数的概念，底层只是一大串二进制数据在进行运算（在底层就是一大堆寄存器处于开关的工作状态中）。定点数的第一印象容易给人产生是用来表示整数的印象，然而无论是整数还是小数都可以采用定点数来表示，同理整数和小数的概念也是人为规定上去的，FPGA本身不会理解那一大串二进制数是表示整数还是小数，具体的运算法则由编程人员规定好。

1.1 Qm.n的表示方法

本文采用最广泛使用的补码表示形式（默认都懂其他的原码表示和反码表示形式），对应的用来表示有符号数。人为定义小数点的位置。

采用Qm.n量化表示定点数，其中m用来表示小数点前的位宽，包括一位符号位和m-1位整数位，n表示小数位宽。如16位有符号整数可以表示成Q16.0,用来表示小于1的小数则可以表示成Q1.15。对于Qm.n的表示格式，其范围表示如下：

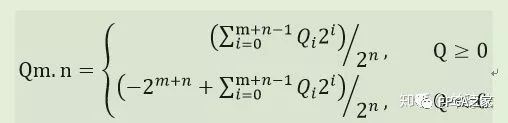
例如，1110整数则表示为Q4.0:（-2^4 + 2^3 + 2^2 +0）/2^0= -2，1110有两位小数则表示为Q2.2：（-2^4+2^3+2^1+0）/2^2 = -0.5。下表对应表示16位二进制补码表示的数的范围。

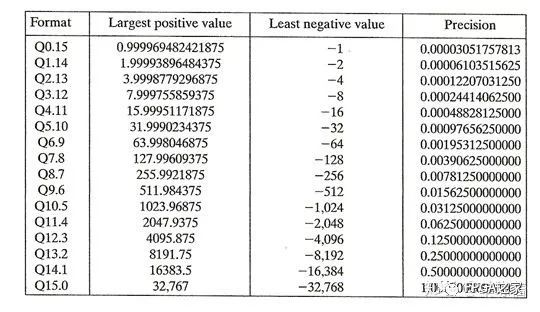
1.1 浮点数的定点化

浮点数的定点化涉及到量化方法。量化的过程可以表示为：

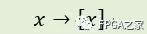
量化方法主要有两种：尾部截断舍弃法和尾部四舍五入法。

对于尾部截断舍弃法，顾名思义则是丢弃掉尾部不能表示的部分。假设将浮点数表示成8位Q3.5的定点数，则表示过程如下（对3.2和-3.2进行定点化）：

[3.2] = floor(3.2*2^5) = floor(102.4) = 102 = 01100110

[-3.2] = floor(-3.2*2^5) = floor(-102.4) = -103 = 10011001

采用MATLAB可以做如下实现：

dec2bin(floor(3.2*2^5), 8) = 01100110

dec2bin(2^8+floor(-3.2*2^5), 8) = 10011001

对于四舍五入法，则对应的过程表示如下：

[3.2] = round(3.2*2^5) = round(102.4) =102 = 01100110

[-3.2]=round(-3.2*2^5) = round(-102.4)= -102 = 10011010

采用MATLAB可以做如下实现：

dec2bin(round(3.2*2^5), 8) = 01100110

dec2bin(2^8+round(-3.2*2^5), 8) = 10011010

由于采用四舍五入方法还需要进行尾部数据的判断，因此通常使用中，如无特别需求，多采用尾部截断舍弃法。

3. 浮点数表示

在FPGA运算中，浮点数无论是表示方法、资源占用还是运算法则都比定点数复杂得多。但另一方面，基于FGPA 的实现的算法性能严重依赖于算法的数值精度表示，很多时候在信号处理中，数值的动态范围过大，采用一般的定点算法往往无法满足这样大的动态范围，而且定点算法经过精打细算之后，算法的小数位和整数位是固定的，表示的范围同样是固定的，无法在作调节，后续一旦有所修改，整个算法实现过程需要重新进行计算仿真设计，这样的后期维护成本太高，简直是牵一发而动全身。对于cpu处理器来说，浮点格式基本上会采用IEEE 754制定的标准单精度或双精度格式。而对于FPGA来说，由于其强大的灵活性，虽然也是按照IEEE 754标准实现浮点数表示，但是却可以对尾数和指数的位宽作修改。

IEEE 754定制的浮点格式在存储方面有着很完美的形式，可以最大限度表示数的动态范围的同时，减少存储资源，但是实际参与运算时并没那么直接，需要经过相应的换算。因此可利用FPGA的灵活性，自定义浮点数格式。

3.1 自定义浮点格式表示

不像根据IEEE 754[45] 标准所设计的32-bit和64-bit标准浮点格式，本论文的自定义浮点由位宽可配置的指数（Exponent）和尾数（Mantissa）两部分组成。指数和尾数部分都是有符号定点数。作为一个例子，我们采用标准双精度浮点格式和自定义浮点格式之间进行对比。标准双精度浮点数可以表示如下等式：

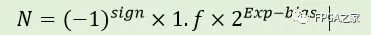
其中1.f表示52-bit尾数；Exp 表示存储起来的指数值；bias 表示偏置，对于标准双精度浮点，改值为1023；Exp-bias 表示实际的指数值。标准格式表示如图(a) 所示。然而，对于自定义浮点格式表示的数的实际值如下：

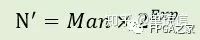
其中，Man 表示的尾数是52-bit有符号定点数，表示的实际值为0.1b49b48...b2b1b0 或者1.0b49b48...b2b1b0。而Exp 表示实际指数值。具体格式表示如图(b)所示。

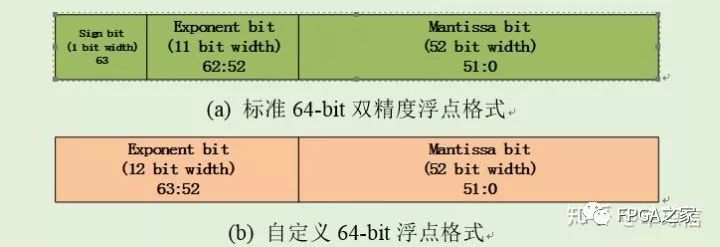
自定义浮点算法的其中一个优点是指数部分和尾数部分的位宽都是可配置的，设计者可以在算法精度要求和资源消耗方面进行权衡。而现存的由XILINX 提供的浮点运算IP 核是基于IEEE 754标准的，在每一次四则运算之后（如加法或乘法之后）都会进行一个格式化运算。而格式化运算占比的硬件资源消耗很大。无疑，如果存在多次连续加法运算或者乘加运算，这样的运算方式是资源消耗严重的。而本文所提出的自定义浮点算法则是整合的乘加运算和连续加法运算，尽量减少格式化操作，从而减少资源消耗。

1.1 定点数转自定义浮点格式

相比较于标准浮点格式的转换，定点数转成上文描述的自定义浮点格式相对来说简单许多，只需要经过简单的规格化，假设定点数为Qm.n，将其转换为指数位宽为E，尾数位宽为M，其过程可以描述如下：

输入：定点数Qm.n，则初始指数值为m，尾数Q1.(m+n-1)；

规格化：计算符号位个数，假设计算得符号位个数为k；

输出：指数输出值为m-k，尾数从m+n-k作为最高位开始截位，截取M位，如果不够长，则从最低位开始补零，补足到M位长度输出。

这里唯一需要再次说明的是，如何计算符号位的个数，最简单的方法就是采用一个for循环，for循环里边使用一个计数器（初始值为1）和比较判断器，从次高位开始与最高位做比较，如果相同（同为1或者同为0），则计数器加1，以此类推下去。这里使用MATLAB，按照比特级别仿真，打包成一个函数，如下：

 

function k = dupSign_cal(u)%  u: 定点数输入
% k：计算符号位个数
bit_len = get(u, 'WordLenght');
SignBit = bitget(u, bit_len);
count = 1;
for i = bit_len-1:-1:1
 if bitget(u, i) == SignBit 
   count = count+1;
 else
   break;
 end
end

 

当然，无论是verilog里边的for循环还是vhdl里边的for循环，并非软件中for的概念意义，实际上FPGA综合时会将for循环全部展开，因此这里如果定点数太长，则for循环不但消耗的资源多，而且非常容易造成时序不过关（想想在规定的一个或两个时钟里边完成几十比特一比特一比特的比对）。因此如果定点位宽太长，则应该想更多的办法来完成该过程，FPGA节省时间的方法无外乎增加资源，一个for循环不行，并行多个for循环嘛。　　

      审核编辑：彭静