双端口谐振器的Q值提取方法

微波谐振器是微波工程里使用非常普遍的一类无源器件，它可以构成振荡器、滤波器的一部分，也可以用于各种测量或传感系统中（比如介电常数、表面阻抗测量系统，温湿度传感系统等）。谐振频率和品质因子（简称Q值）是衡量微波谐振器特性最为关键的参数。本文对微波谐振器的Q值获取方法进行探讨。总体上而言，Q值提取方法可以分为频域法和时域法。3dB法是最具代表性的频域方法，它需要首先获取3dB带宽，然后计算得到Q值。而时域法则是通过观察激励信号源突然关闭后，依据谐振器输出端口信号的时变特性来获取Q值。本文介绍频域方法。常见的微波谐振器有单端口和双端口两种。前者需要测量谐振器的S11来获取Q值，而后者则是通过测量S21来获取Q值。本文探讨双端口谐振器的Q值提取方法。

传统的3dB法提取Q值的过程如下图所示：横坐标为频率，纵坐标为S21幅度，S21幅度最大值对应的频率即为谐振频率f0，然后分别在f0的左侧和右侧找到3dB带宽频点f1和f2，这两个频点对应的S21幅度比S21幅度的最大值低3dB，到此即可得到3dB带宽为(f2-f1)，于是谐振器的有载Q值可由QL=f0/(f2-f1)计算得到，无载Q值Q0可由有载Q值和S21幅度最大值|S21|max按照Q0=QL/(1-|S21|max)计算得到（注意，这里的|S21|max须是线性值，其数值为0至1之间的某个数）。举例如下，假设谐振器谐振频率为3GHz，3dB带宽为5MHz，则有载Q值为3GHz/5MHz=600，又假设谐振器在谐振频率处的插损为40dB，则|S21|max=10^(-40/20)=0.01，于是无载Q值Q0=600/(1-0.01)=606。

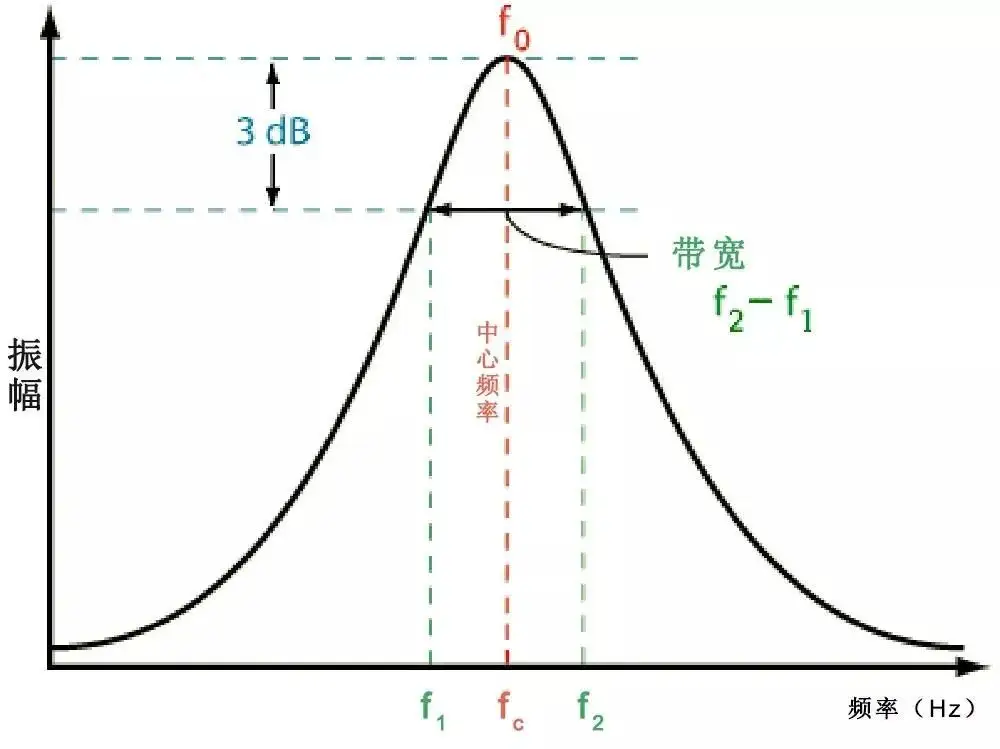
依据上述3dB法求解Q值的过程，如果获得了双端口谐振器的S21幅度随频率变化的数据，可以利用下述MATLAB代码求解Q值：

simu_data01=load( 'S21_dB_freq.txt'); % 导入S21数据,第一列为频率,第二列为dB形式的S21

f=simu_data01(:,1); % 频率

S21=simu_data01(:,2); % S21，dB

[S21m, S21m_location]=max(S21);% 找到S21幅度最大值及其位置

f_center=f(S21m_location); % 谐振频率；

S21dB_center=S21(S21m_location); % 找到dB形式的S21幅度最大值

S21_center=10^(S21dB_center/20); % 找到线性形式的S21幅度最大值

% 找到谐振频率左侧3dB带宽对应的频点

a01=find(S21(1:S21m_location)-S21m>-3.1,1);

a02=find(S21(1:S21m_location)-S21m>-0.1,1);

f_low=interp1(S21(a01:a02),f(a01:a02),S21m-3,'spline');

% 找到谐振频率右侧3dB带宽对应的频点

a01=find(S21(S21m_location:length(S21))-S21m<-3.1,1);

a02=find(S21(S21m_location:length(S21))-S21m<-0.1,1);

f_up=interp1(S21(a02+S21m_location-1+1:a01+S21m_location-1),f(a02+S21m_location-1+1:a01+S21m_location-1),S21m-3,'spline');

% 计算有载Q值

Q_L=f_center/(f_up-f_low);

% 计算无载Q值

g=S21_center/(1-S21_center); % for series RLC circuit

% g=(1-S21_center)/S21_center; % for parallel RLC circuit

Q_unload=Q_L*(1+g);

用传统的3dB法测量Q值时，需要进行扫频测试，且要求扫频带宽至少是3dB带宽的一定倍数（比如1.5倍或更大）。因此，这种测试方法对扫频信号源的扫频带宽有一定的要求，而且较大的扫频带宽一般也就意味着更长的测试时间。所以，如果能够减小扫频带宽，则可能有助于降低扫频源的成本并缩短扫频时长也就是缩减测试时长，进而降低测试成本。本文即探讨此种可能性。

在文献《Measurement of resonant frequency and quality factor of microwave resonators: Comparison of methods》中，给出了双端口谐振器的S21幅度随频率变化的规律如下： 

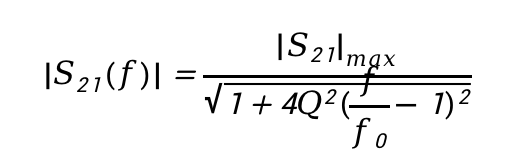
由上式可知，如下3个参数决定了谐振器传输曲线的形状和位置：S21幅度最大值、品质因子、谐振频率。如果做一些计算实验，不难发现，参数S21幅度最大值影响传输曲线在纵坐标上的位置，品质因子影响传输曲线的“胖瘦”，而谐振频率影响传输曲线在横坐标上的位置。接下来，我们首先检验上式是否能够描述常见谐振器的传输曲线；然后，我们利用上式构造了若干谐振器传输曲线，然后观察谐振器传输曲线的1dB带宽是否和3dB带宽存在某种定量关联性。如果这种关联性是存在的，则可以通过1dB带宽的测量间接获取3dB带宽，并最终实现1dB法获取谐振器Q值。

这里，我们选取了常见的圆柱谐振腔、同轴谐振腔、矩形谐振腔、微带环形谐振器以及准光腔作为演示案例。

第一个圆柱谐振腔的三维剖面模型及其传输曲线仿真结果如下所示。这是一个谐振频率约为10GHz的谐振腔。

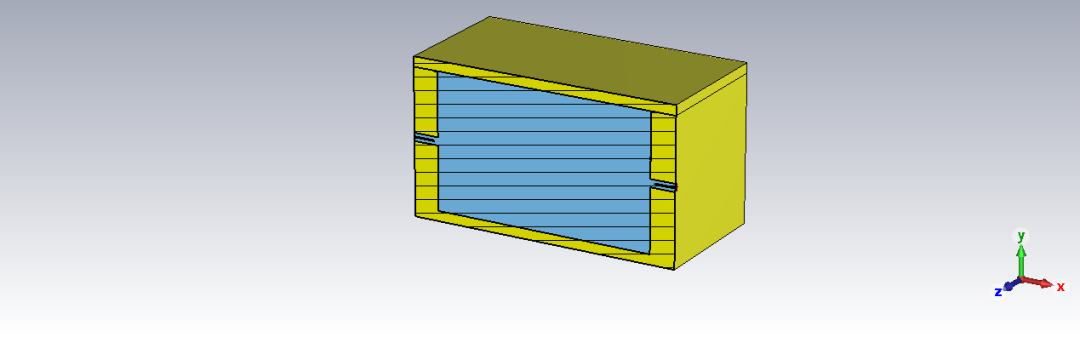
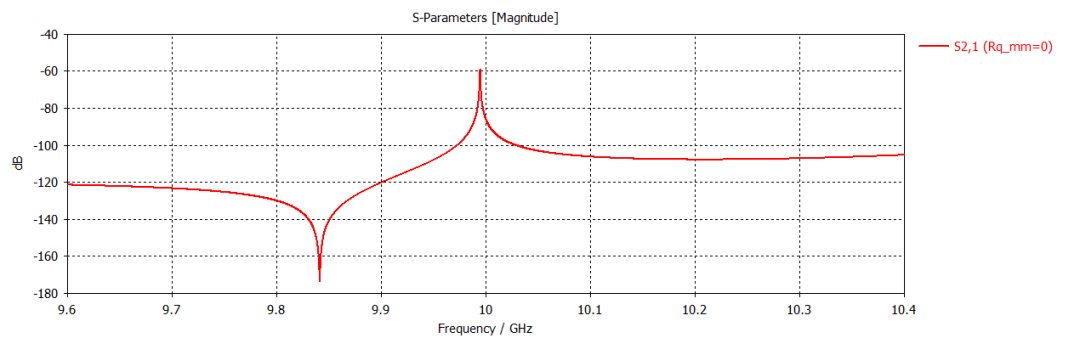
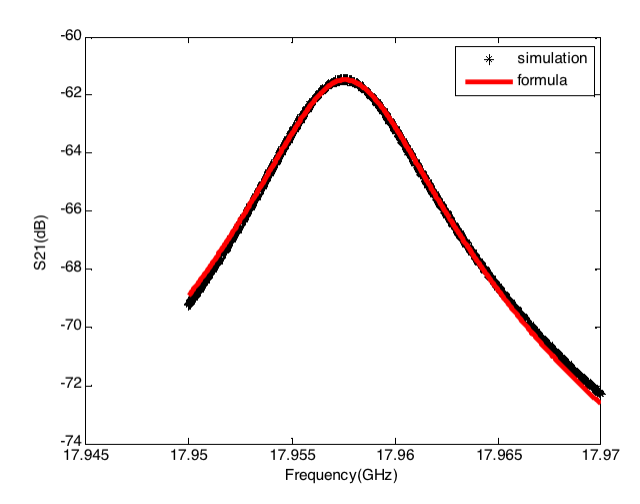
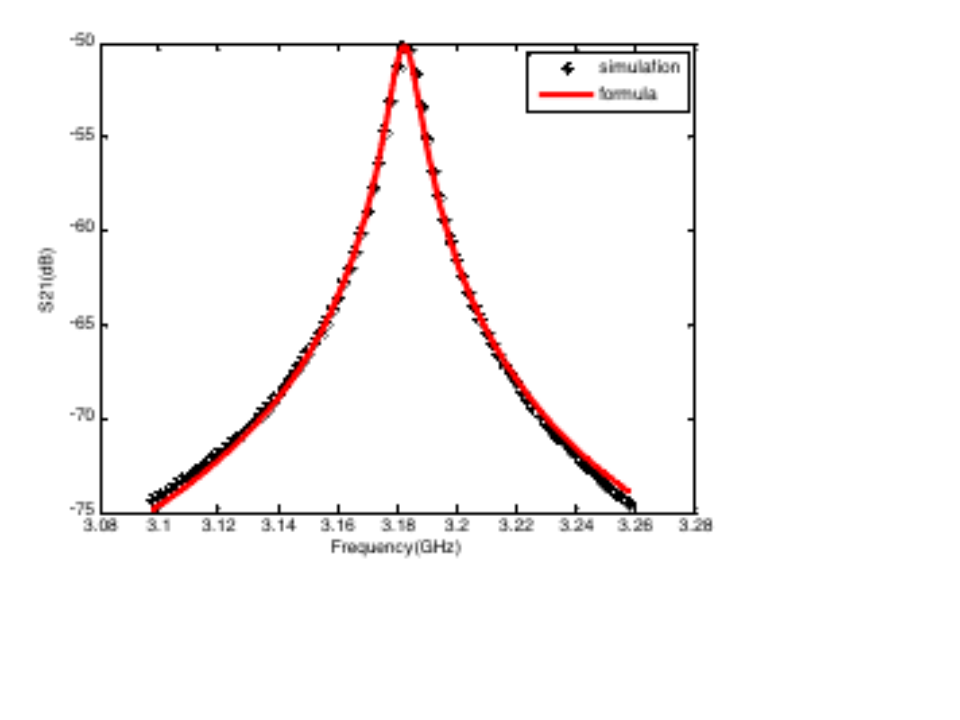
运用前述公式，对上图得到的谐振峰仿真结果进行拟合，所得结果如下。可以看到，拟合结果与仿真结果吻合良好。其余几种腔体也得到了类似的拟合效果，这表明前述公式可以用于描述双端口谐振器的传输曲线。

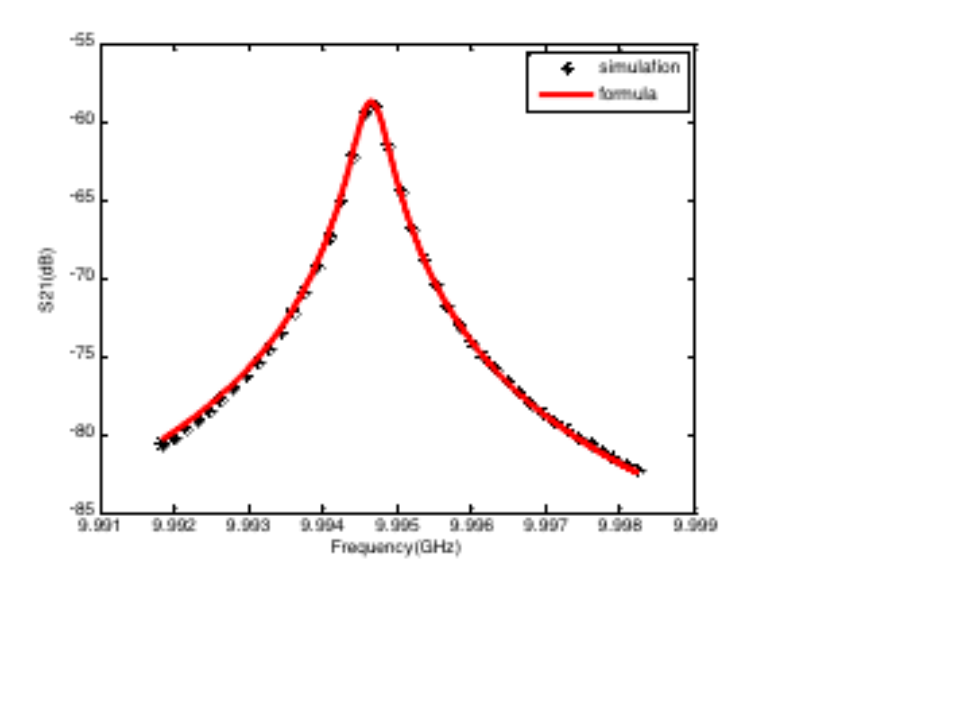
第二个圆柱谐振腔案例是一个谐振频率约为18GHz的腔体，其相关结果如下所示。

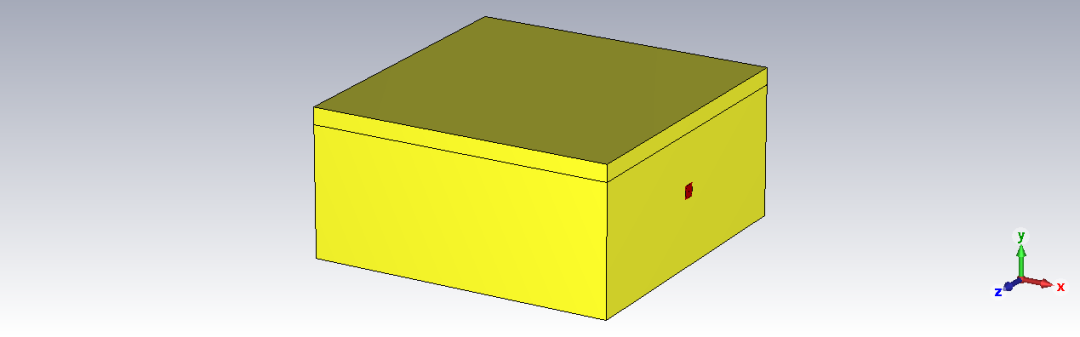
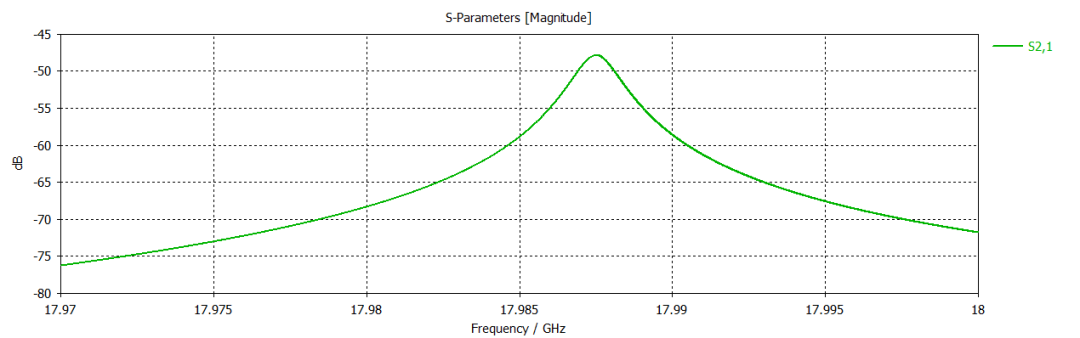
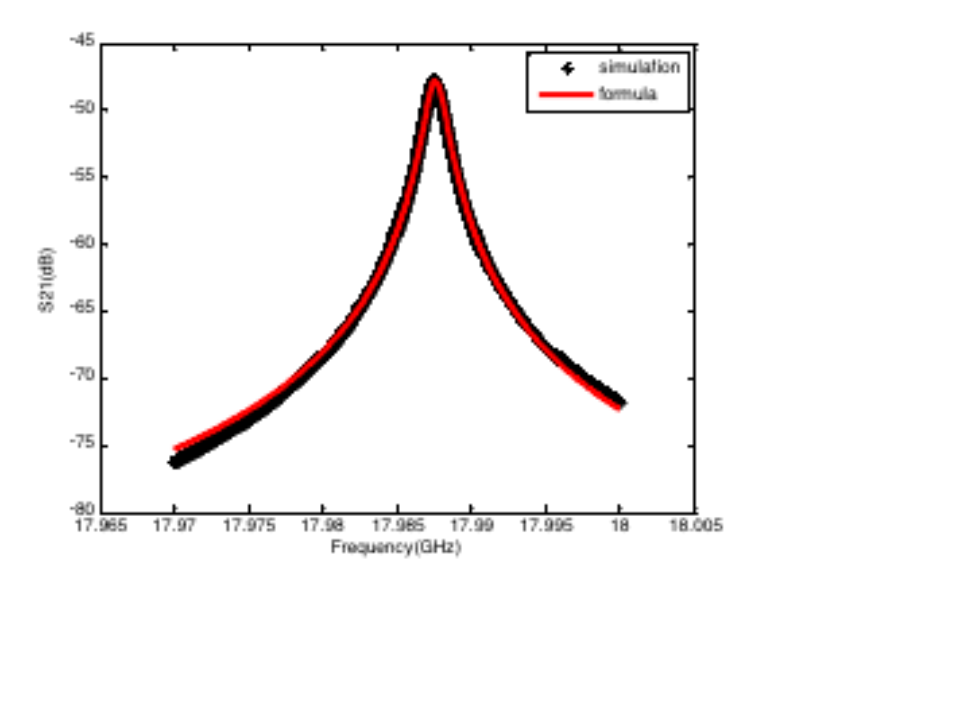
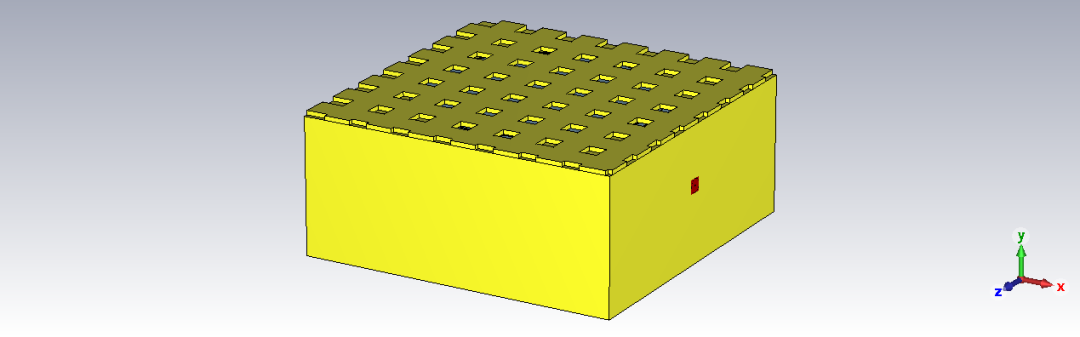
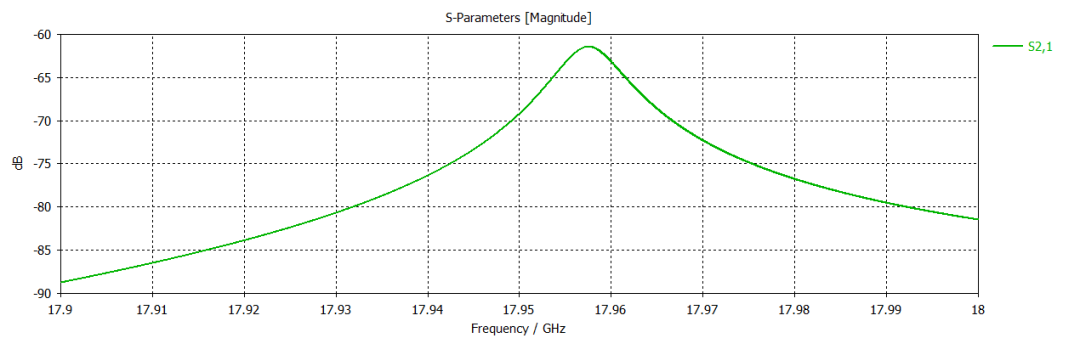
第三个圆柱谐振腔案例仍是一个谐振频率约为18GHz的腔体，但是该腔体的上端板排布有周期性的方孔，其模型及相关结果如下所示。

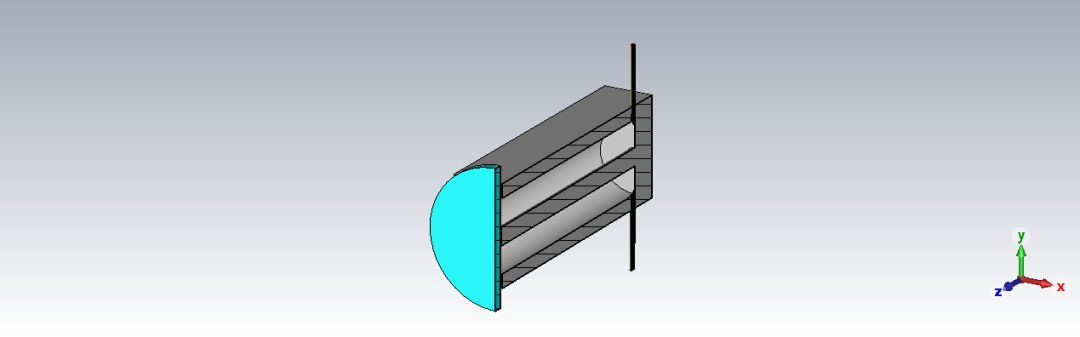
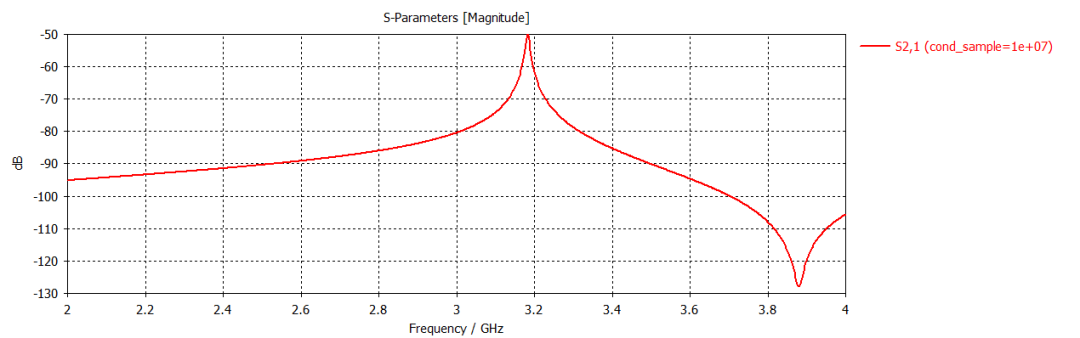
同轴谐振腔案例的相关结果如下所示。这是一个谐振频率约为3.2GHz的腔体。

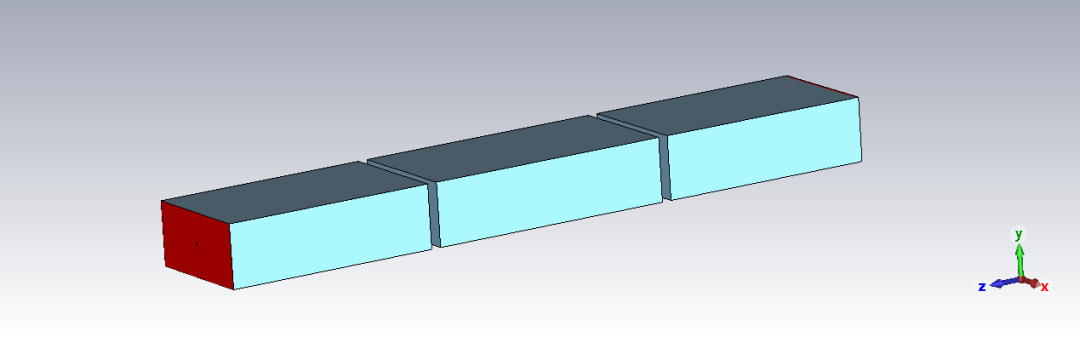
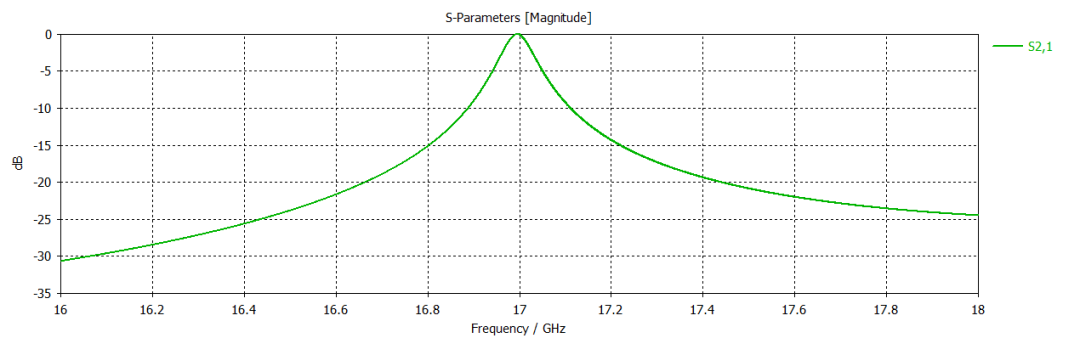
矩形谐振腔案例的相关结果如下所示。这是一个谐振频率约为17GHz的腔体。

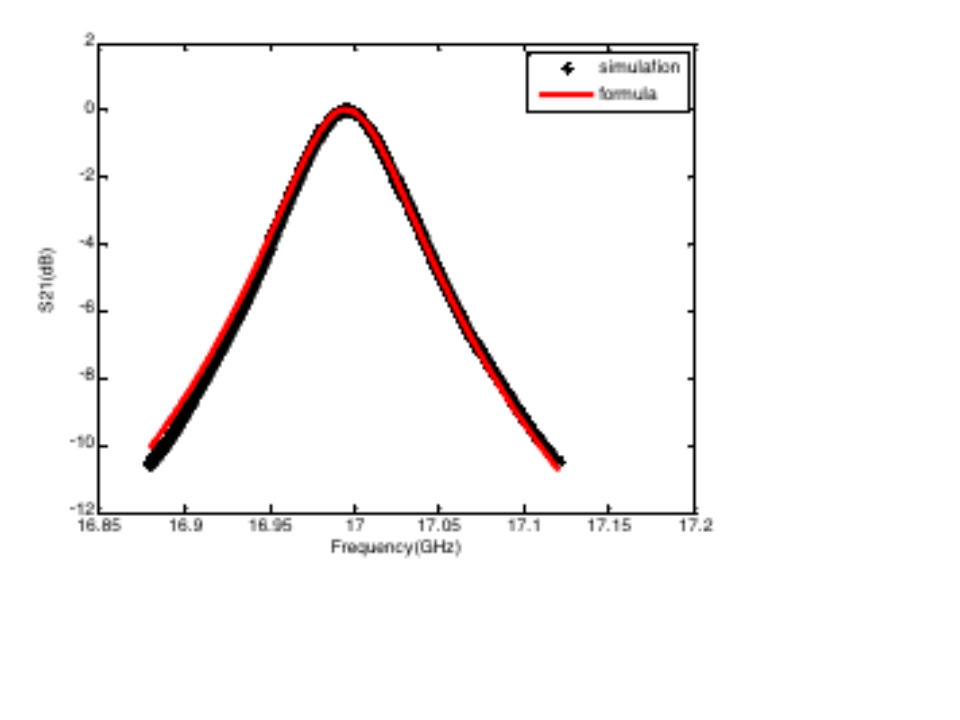
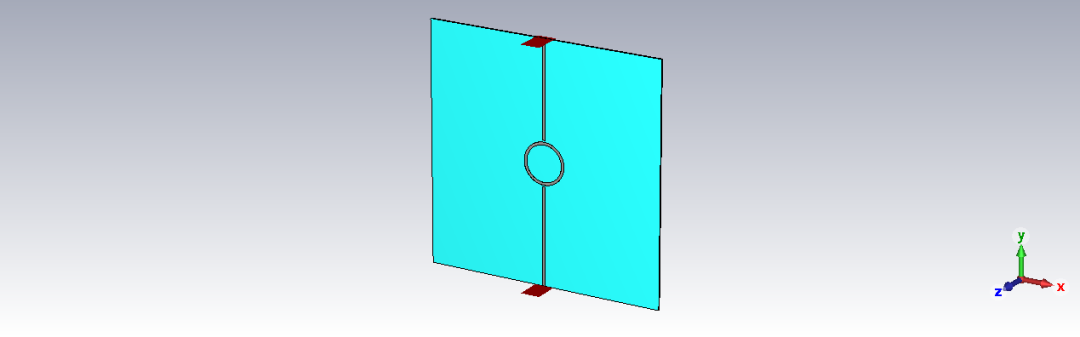
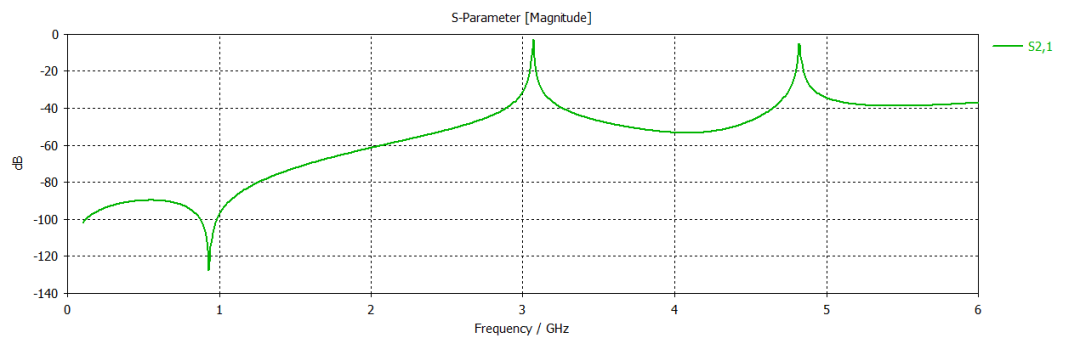
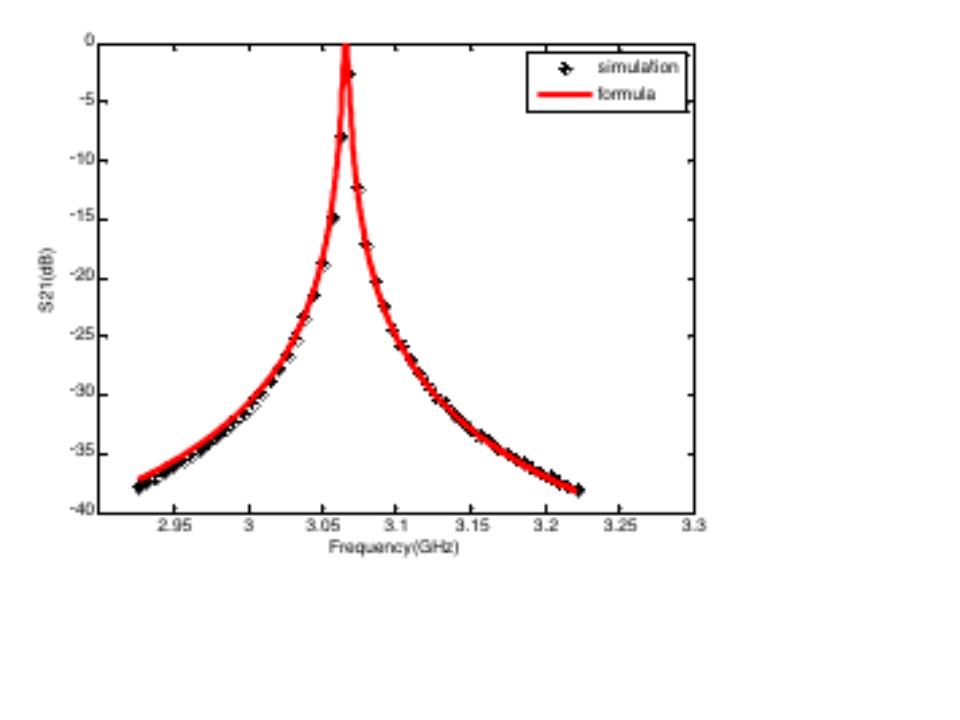
微带环形谐振器案例的相关结果如下所示。在CST仿真频段内出现了2个谐振峰，我们对第一个谐振峰也就是3GHz附近的谐振峰进行了拟合。

准光腔案例的相关结果如下所示。其谐振频率约为30GHz。

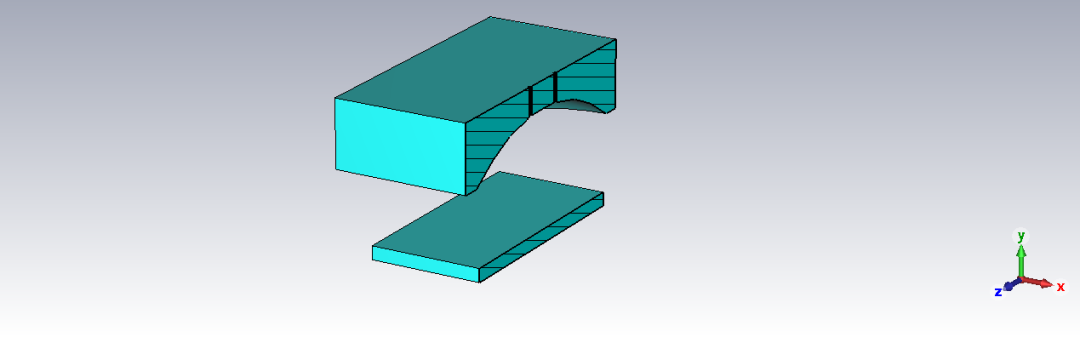
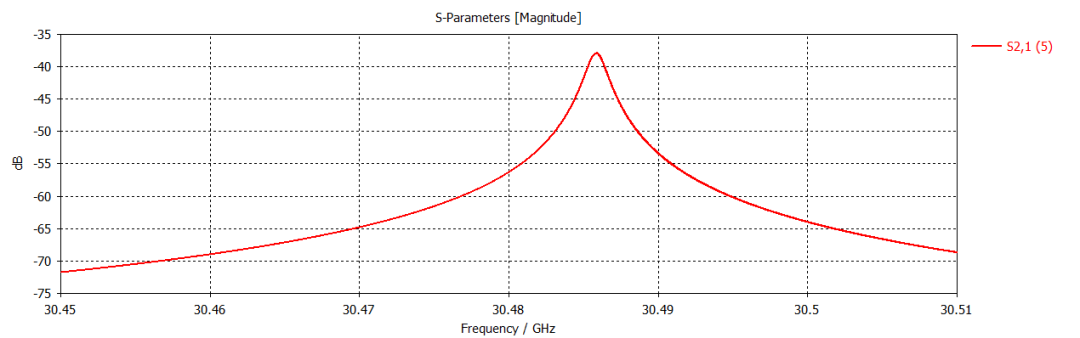
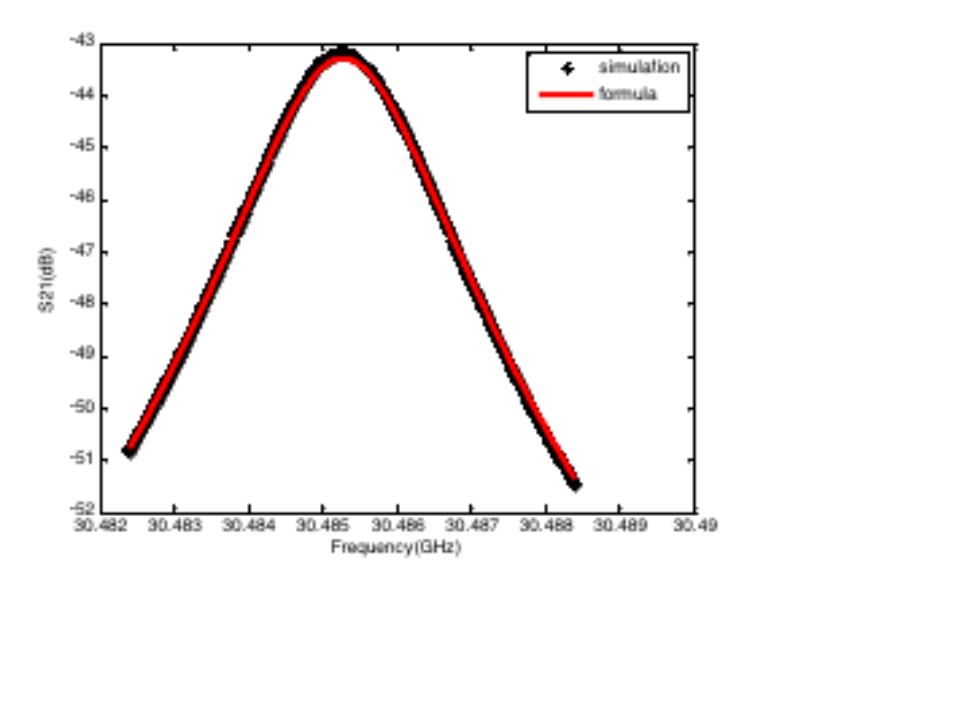
通过上述7个案例，表明前述公式可以描述常见谐振器的传输曲线。以下是上述拟合过程所采用的典型MATLAB代码：

S21_data_simu=textread('simulation_data.txt','','headerlines',3); % 导入CST仿真数据

nn01=2450; % 设定拟合频段的起始频点

nn02=2490; % 设定拟合频段的终止频点

freq_simu=S21_data_simu(nn01:nn02,1); % 频率

S21_dB_simu=S21_data_simu(nn01:nn02,2); % dB形式的S21

S21_linear_simu=10.^(S21_dB_simu./20); % 线性形式的S21

figure(1);plot(freq_simu,S21_dB_simu,'k*');hold on; % 绘制仿真数据

% 以下是扫参拟合

a_sweep=linspace(0.0011,0.0013,100); 

b_sweep=linspace(1e4,3e4,50);

c_sweep=linspace(9.994,9.995,50);

error01=1e4;

opti_num=[0 0 0];

for nnfor01=1:length(a_sweep)

    for nnfor02=1:length(b_sweep)

        for nnfor03=1:length(c_sweep)

a=a_sweep(nnfor01);

b=b_sweep(nnfor02);

c=c_sweep(nnfor03);

x=freq_simu;

y=a./sqrt(1+4.*b.^2.*(x./c-1).^2);

error_for01=mean(abs(S21_linear_simu-y));

if error_for01

    error01=error_for01;

    opti_num=[nnfor01 nnfor02 nnfor03];

end

        end

    end

end

a_opti=a_sweep(opti_num(1));

b_opti=b_sweep(opti_num(2));

c_opti=c_sweep(opti_num(3));

% 依据扫参拟合得到的拟合系数计算传输曲线并绘图

x=linspace(min(freq_simu),max(freq_simu),1e3);

y_opti=a_opti./sqrt(1+4.*b_opti.^2.*(x./c_opti-1).^2);

figure(1);plot(x,20.*log10(y_opti),'r-','linewidth',3);

xlabel('Frequency(GHz)');ylabel('S21(dB)');

legend('simulation','formula');

接下来，我们利用前述公式构造若干传输曲线并观察1dB带宽和3dB带宽的关系。S21幅度最大值取值0.1、谐振频率取值3GHz、品质因子从10扫描至1000万时，得到的1dB带宽与3dB带宽之比如下图——恒为0.51。当S21幅度最大值、谐振频率为其它取值时，得到了相同的结果——1dB带宽与3dB带宽之比恒为0.51。这意味着，实际测量谐振器Q值时，可以先测得1dB带宽，然后用此1dB带宽乘以系数1/0.51=1.961，即可得到谐振器的3dB带宽，进而得到谐振器Q值。换言之，1dB带宽约为3dB带宽的一半。这样，扫频源的扫频范围可以减半，或者说扫频时长可以缩至原先的一半。

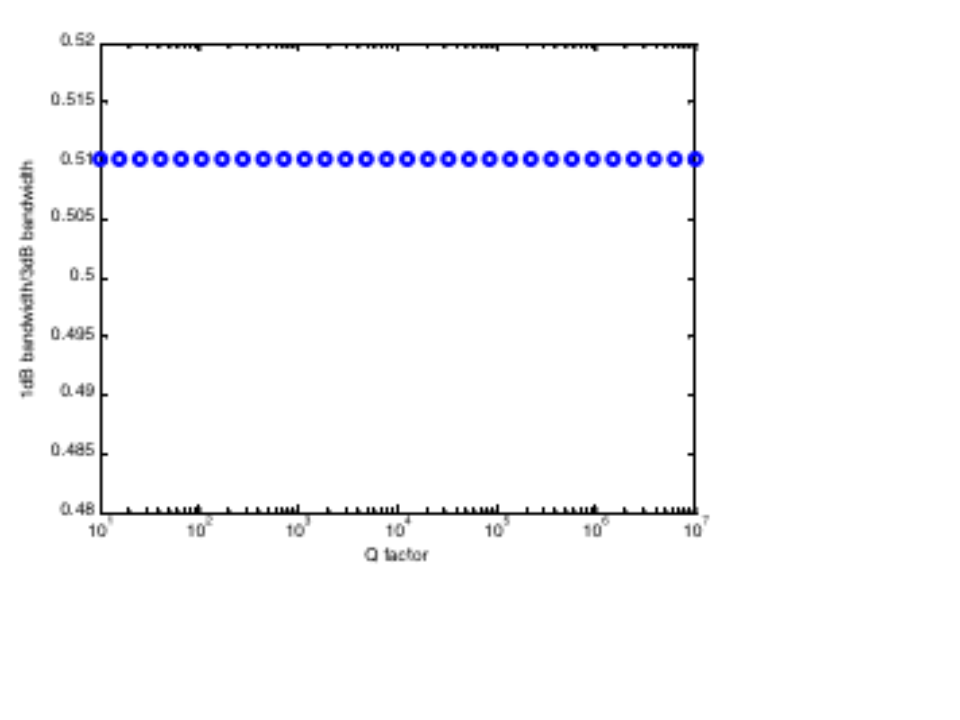
上图对应的MATLAB代码如下：

Q_sweep=logspace(1,7,30);

for nn01=1:length(Q_sweep)

Q=Q_sweep(nn01);

f0_GHz=3;

abs_S21=0.1;

S21_dB=20*log10(abs_S21);

bandwidth01=f0_GHz/Q;

f_GHz=linspace(f0_GHz-2*bandwidth01,f0_GHz+2*bandwidth01,1e3);

real_S21=abs_S21./(1+4.*Q.^2.*(f_GHz./f0_GHz-1).^2);

imag_S21=-abs_S21.*2.*Q.*(f_GHz./f0_GHz-1)./(1+4.*Q.^2.*(f_GHz./f0_GHz-1).^2);

mag_S21=sqrt(real_S21.^2+imag_S21.^2);

mag_S21_dB=20.*log10(mag_S21);

[S21_dB_max,S21_dB_num]=max(mag_S21_dB);

% 3dB 

f_GHz_left_3dB=interp1(mag_S21_dB(1:S21_dB_num-1),f_GHz(1:S21_dB_num-1),S21_dB_max-3,'spline');

f_GHz_righ_3dB=interp1(mag_S21_dB(S21_dB_num+1:length(f_GHz)),f_GHz(S21_dB_num+1:length(f_GHz)),S21_dB_max-3,'spline');

delta_f_3dB=f_GHz_righ_3dB-f_GHz_left_3dB;

Q_3dB(nn01)=f0_GHz/delta_f_3dB;

% 1dB 

f_GHz_left_1dB=interp1(mag_S21_dB(1:S21_dB_num-1),f_GHz(1:S21_dB_num-1),S21_dB_max-1,'spline');

f_GHz_righ_1dB=interp1(mag_S21_dB(S21_dB_num+1:length(f_GHz)),f_GHz(S21_dB_num+1:length(f_GHz)),S21_dB_max-1,'spline');

delta_f_1dB=f_GHz_righ_1dB-f_GHz_left_1dB;

Q_1dB(nn01)=f0_GHz/delta_f_1dB;

end

ratio_Q=Q_3dB./Q_1dB;

semilogx(Q_sweep,ratio_Q,'bo','linewidth',3);

xlabel('Q factor');ylabel('1dB bandwidth/3dB bandwidth');

axis([10,1e7,0.48,0.52]);

　　审核编辑：汤梓红