

基本的CS拓扑结构电路
电源/新能源
描述
简单电路的学习是研究复杂电路的起点,因为复杂电路就是由一个个简单电路组合起来的。
所以,先把基础打牢靠。
电流源:
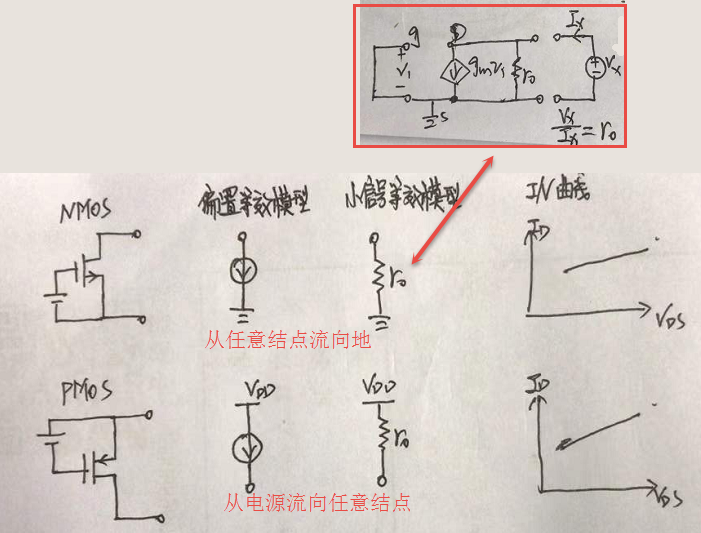
diode-connected MOS
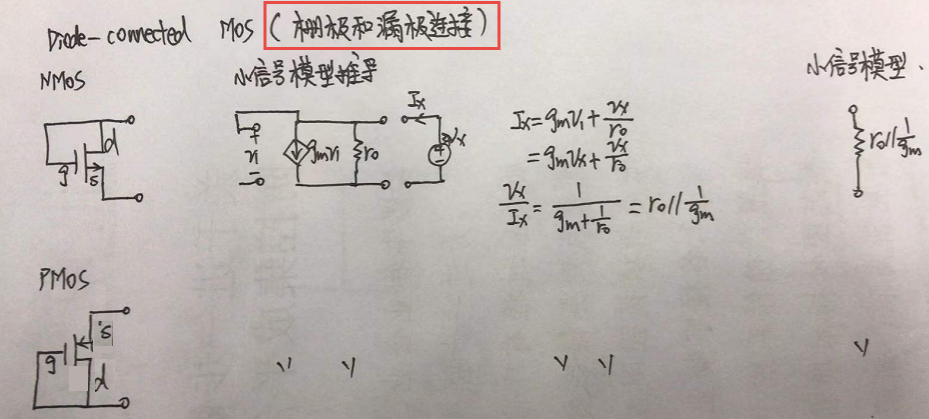
Degenerated CS stage
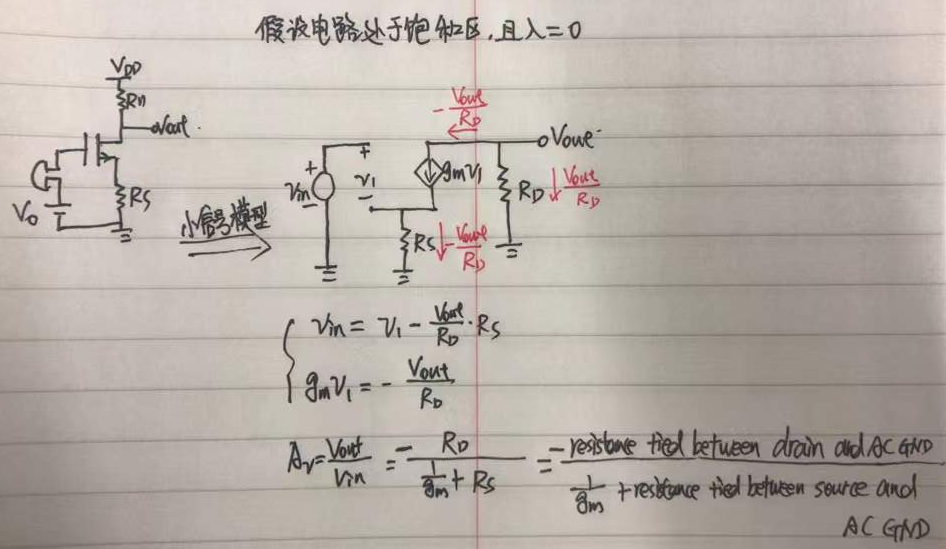
基本的CS拓扑结构,就能把信号放大,为啥要折腾出这么多形形色色的电路出来呢?
费这么大力气,当然有他的好处在的。
比如说,电流源。
理想的电流源有这样一个特点,在偏置模型中,能提供偏置点,在小信号模型中,又有无穷大的电阻。
基本的CS拓扑结构,其增益为:
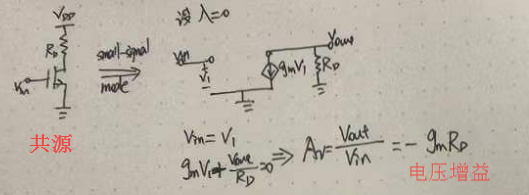
可以看到,RD的大小,限定了共源放大器的增益。但是你想把RD提高,放大器的工作状态又不答应。RD提得太高,MOS管就可能进入线性区。所以,想要靠提高RD来提升增益,程度非常有限。
那怎么办呢?
这时候,电流源就有了用武之地了。用电流源把RD一替,增益就能变高一大截。那有人会说,电流源的电阻等效于无穷大了,是不是我就有无穷大的增益了?别急,还有沟道调制效应要考虑呢。
如果考虑上沟道调制效应,则:
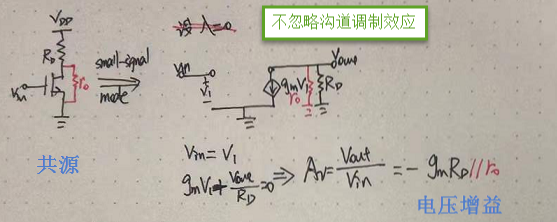
用电流源替代RD,则:
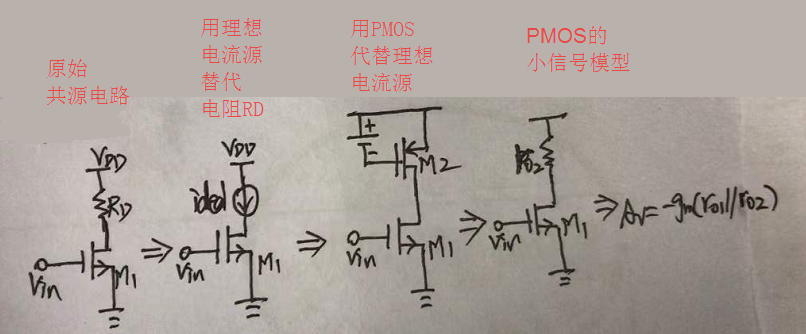
再说diode-connected MOS
由上面推导可知,CS放大器的增益,往往和gm有关。
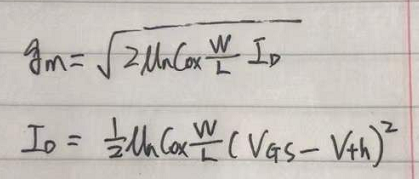
也就是说,gm受很多因素影响:
(1) 不同晶圆之间(un,Cox,Vth),gm的大小也不同
不同wafer之间,掺杂浓度啥的,总归会有点变化,这就会导致un,Cox,Vth的变化,从而导致gm不一样
(2) 电压大小的不同,也会导致gm的不同
比如说用电池的设备,电池在充满电和用了一些电时,其输出电压可能也会有变化,这也会导致gm的不同
(3) 温度的影响
温度不同,电子和空穴的迁移率也会变化,gm的大小也会不同
(4) 信号的大小
以上的小信号模型都是假定输入信号非常小的时候,如果输入信号变大,则ID的变化也会比较大,则gm的变化也比较大。
所以,电路设计者们会寻找一种能降低gm受外部因素影响的结构。
而diode-connected MOS就是这样一个电路结构的基础。
比如说下图,通过用diode-connected MOS来替代RD后,增益就只与管子的尺寸有关了,而这个就受上述几个因素的影响就很小了。
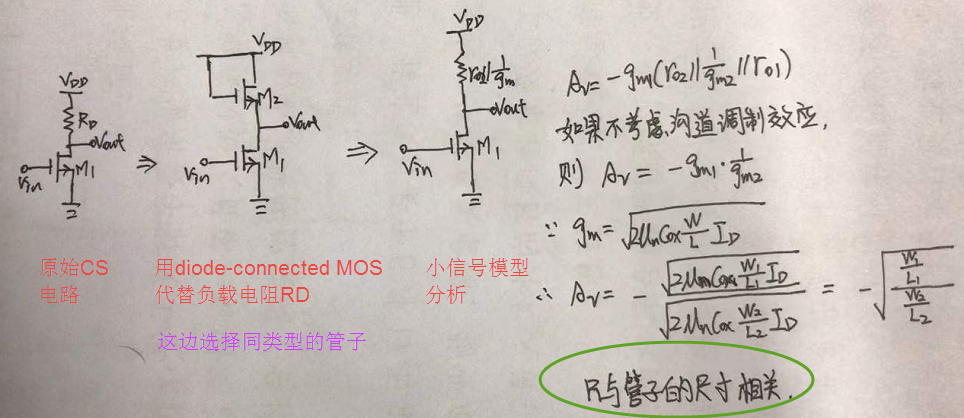
再说degenerated CS stage
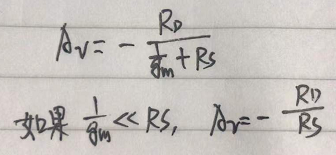
如果,创造条件,使得1/gm<
而且,就算没能创造条件,使得可以忽略gm,但由于RS的存在,也降低了gm对电压增益的影响。
但是,在源极增加RS,也带来了一个缺点,就是时电压增益降低了。
不过,工程师嘛,永远都是游走在各个矛盾中间,努力做着折中。
在源极增加RS还有一个功能,就是使MOS管形成的非电流源更接近于理想电流源。
理想电流源的阻抗为无穷大,但是基本MOS管形成的电流源的阻抗则为r0。但是在源极增加Rs, 则能极大的增加电流源的阻抗。
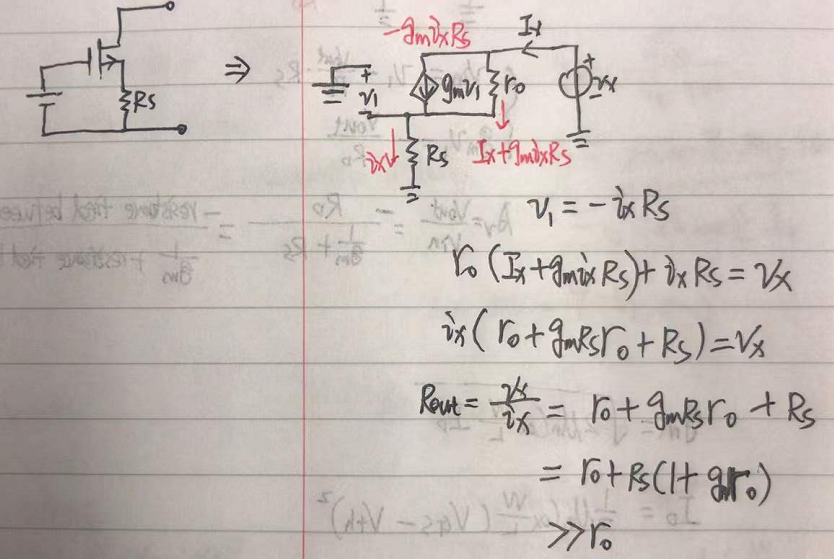
-
常见的电路拓扑结构2024-05-29 721
-
buck电路的拓扑结构 buck电路临界条件怎么来的2024-02-14 4492
-
电路拓扑结构方案介绍2023-11-14 304
-
拓扑视图与实际拓扑结构间的差异2023-09-10 1937
-
BOOST电路拓扑结构介绍2023-03-22 3413
-
拓扑结构是什么意思2023-03-07 5325
-
理解拓扑结构2021-11-17 1351
-
基于拓扑结构的升压Boost2021-11-11 2315
-
电源三大拓扑中的Boost拓扑结构2021-10-28 2865
-
SDRAM的电源系统及拓扑结构2018-12-03 2655
-
什么是电路拓扑结构_多种pfc电路的拓扑结构介绍2018-01-23 55115
-
Fliege陷波滤波器的拓扑结构2010-09-03 2506
-
全桥电路基础的拓扑结构2010-06-24 3656
-
拓扑结构,拓扑结构有哪些类型?2010-03-22 13191
全部0条评论

快来发表一下你的评论吧 !

