

狭义相对论下的静电力
描述
一般来说,当我们说到磁性时,我们认为它是由移动电荷产生的磁力线。假设有一根导线,并且有电流通过,就会产生一条围绕电线的磁场线。如果我们在此区域引入一个移动的带电粒子,那么该粒子将由于磁场的存在而受到洛伦兹力。现在,我们把洛伦兹力的概念放在一边,因为接下来我们将用另一种方式来解释这个力:狭义相对论下的静电力。
想象一下,我们有一根导线和一个带电粒子,粒子的速度为u。
情景一:导线中的正电荷和负电荷静止不动,它们的电荷线密度都是λ₀,因此互相抵消不会对外界的带电粒子产生静电力。
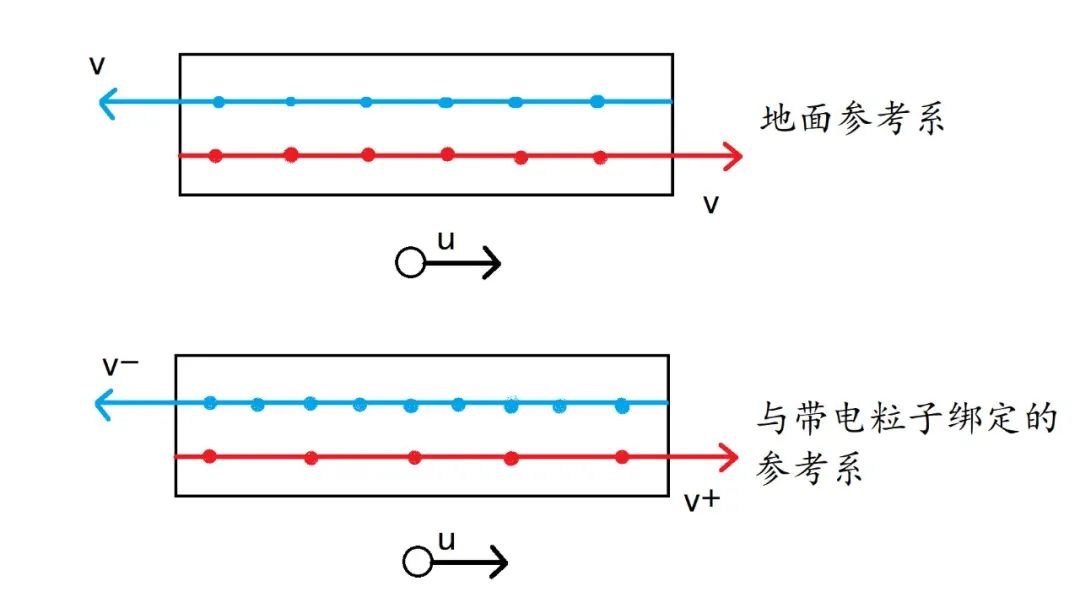
情景二,我们让导线产生电流:正电荷以速度v向右移动,负电荷以速度v向左移动。虽然这个模型有点不实际,但计算很好用。从地面观察者来看,由于狭义相对论的尺缩效应,电荷之间的距离会缩小,因此线密度会变大。由于正电荷和负电荷速度大小一样,因此它们的线密度都为λ,净电荷密度为零,不会对外界带电粒子产生静电力。
现在,我们把参考系和导线外的带电粒子绑定在一起。在这个参考系下的观察者会看到,正电荷的移动速度大小v+与负电荷的移动速度大小v-不同,因此两个正电荷之间的距离与两个负电荷之间的距离不同,导致正电荷的线密度λ+就与负电荷的线密度λ-不同。所以,导线的横截面就会有净电荷产生,会对导线外的带电粒子产生静电力。
把以上的等式结合起来,我们能得到净电荷密度λ_t的公式:
由上式我们可以看出,确实电荷密度不为零,所以会产生电场,带电粒子就会受到静电力。闭合曲面内的电荷分布与产生的电场之间的关系可以由高斯定理算得。因此,我们沿着导线做一个半径为r的圆柱面,根据高斯定理,可以得到带电粒子处的场强,然后就可以得到粒子所受的静电力:
接下来,我们要用到麦克斯韦方程组推导出来的光速公式c²=1/ε₀μ₀和上述提到的电流公式I=2λv,对受力公式进行替换,可以得到:
请注意,这里的F'是在和带电粒子绑定的坐标系下,我们需要把它转换到地面观察者的坐标系。
这就是与洛伦兹力相同的静电力,只不过在地面观察者看来,这像是导线电流产生的磁场而导致的力。我们还可以让它和洛伦兹力的公式相等,就能得到导线产生的磁场强度:
这看起来是不是很熟悉,就是我们高中学过的毕奥—萨伐尔定律。
审核编辑:汤梓红
-
晶圆表面清洗静电力产生原因2025-05-28 737
-
静电力、电场力、磁场力和电磁力的作用2023-09-15 17036
-
一种面向视频感知的静电力触觉渲染方法2017-12-22 801
-
意大利科学家发现超光速中微子挑战相对论2011-09-26 1215
-
用快速电子验证相对论效应2010-07-16 779
-
高效率超辐射相对论返波管2010-05-13 2449
-
无外加引导磁场相对论返波振荡器粒子模拟2010-03-05 460
-
自适应线性神经元方法同轴相对论返波管高频特性的数值分析2009-10-29 723
-
相对论磁控管的实验研究2009-10-26 454
-
同轴型相对论返波管的粒子模拟研究2009-10-21 1753
全部0条评论

快来发表一下你的评论吧 !

