图像清晰度的评价方法

图像清晰度是衡量图像质量的一个重要指标，对于相机来说，其一般工作在无参考图像的模式下，所以在拍照时需要进行对焦的控制。对焦不准确，图像就会变得比较模糊不清晰。相机对焦时通过一些清晰度评判指标，控制镜头与CCD的距离，使图像成像清晰。一般对焦时有一个调整的过程，图像从模糊到清晰，再到模糊，确定清晰度峰值，再最终到达最清晰的位置。

常见的图像清晰度评价一般都是基于梯度的方法，本文将介绍五种简单的评价指标，分别是Brenner梯度法、Tenegrad梯度法、laplace梯度法、方差法、能量梯度法。

Brenner梯度法：

计算相差两个单元的两个像素点的灰度差：

FBrenner=∑M∑N(f(x+2,y)−f(x,y))2 式中 (f(x+2,y)−f(x,y))2>Threshold算法准确性取决于阈值的选取。

Tenegrad梯度法：

采用sobel算子分别提取水平和竖直方向的梯度： FTenegrad=∑M∑N|G(x,y)| G(x,y)>Threshold

G(x,y)=Gx(x,y)2+Gy(x,y)2

sobel算子模板如下：

Gx=14⎡⎣⎢−1−2−1000121⎤⎦⎥∗I

Gy=14⎡⎣⎢−101−202−101⎤⎦⎥∗I

Laplace梯度法：

laplace梯度函数与Tenegrad基本一致，只需要用Laplace算子替代sobel算子即可:L=16⎡⎣⎢1414204141⎤⎦⎥∗I

方差法：

聚焦清晰的图像比模糊图像有更大的灰度差异，可用方差函数作为评价:Fvariance=∑M∑N(f(x,y)−E2)

式中E为整幅图像的平均灰度值，该函数对噪声敏感。

能量梯度法：

能量梯度函数适合实时评价图像清晰度：

FBrenner=∑M∑N((f(x+1,y)−f(x,y))2+(f(x,y+1)−f(x,y))2)

实例代码:

 

//方差法


region_to_mean(ImageReduced, Image, ImageMean)


convert_image_type(ImageMean, ImageMean, 'real')


convert_image_type(Image, Image, 'real')


sub_image(Image, ImageMean, ImageSub, 1, 0)


mult_image(ImageSub, ImageSub, ImageResult, 1, 0)


intensity(ImageResult, ImageResult, Value, Deviation)


//拉普拉斯梯度函数


laplace(Image, ImageLaplace4, 'signed', 3, 'n_4')


laplace(Image, ImageLaplace8, 'signed', 3, 'n_8')


add_image(ImageLaplace4, ImageLaplace4, ImageResult1, 1, 0)


add_image(ImageLaplace4, ImageResult1, ImageResult1, 1, 0)


add_image(ImageLaplace8, ImageResult1, ImageResult1, 1, 0)


mult_image(ImageResult1, ImageResult1, ImageResult, 1, 0)


intensity(ImageResult, ImageResult, Value, Deviation)


//能量梯度函数


crop_part(Image, ImagePart00, 0, 0, Width-1, Height-1)


crop_part(Image, ImagePart01, 0, 1, Width-1, Height-1)


crop_part(Image, ImagePart10, 1, 0, Width-1, Height-1)


convert_image_type(ImagePart00, ImagePart00, 'real')


convert_image_type(ImagePart10, ImagePart10, 'real')


convert_image_type(ImagePart01, ImagePart01, 'real')


sub_image(ImagePart10, ImagePart00, ImageSub1, 1, 0)


mult_image(ImageSub1, ImageSub1, ImageResult1, 1, 0)


sub_image(ImagePart01, ImagePart00, ImageSub2, 1, 0)


mult_image(ImageSub2, ImageSub2, ImageResult2, 1, 0)


add_image(ImageResult1, ImageResult2, ImageResult, 1, 0)


intensity(ImageResult, ImageResult, Value, Deviation)


//Brenner梯度法


crop_part(Image, ImagePart00, 0, 0, Width, Height-2)


convert_image_type(ImagePart00, ImagePart00, 'real')


crop_part(Image, ImagePart20, 2, 0, Width, Height-2)


convert_image_type(ImagePart20, ImagePart20, 'real')


sub_image(ImagePart20, ImagePart00, ImageSub, 1, 0)


mult_image(ImageSub, ImageSub, ImageResult, 1, 0)


intensity(ImageResult, ImageResult, Value, Deviation)


//Tenegrad梯度法


sobel_amp(Image, EdgeAmplitude, 'sum_sqrt', 3)


min_max_gray(EdgeAmplitude, EdgeAmplitude, 0, Min, Max, Range)


threshold(EdgeAmplitude, Region1, 20, 255)


region_to_bin(Region1, BinImage, 1, 0, Width, Height)


mult_image(EdgeAmplitude, BinImage, ImageResult4, 1, 0)


mult_image(ImageResult4, ImageResult4, ImageResult, 1, 0)


intensity(ImageResult, ImageResult, Value, Deviation)

 

结果分析:

处理图像为一组对焦从模糊到清晰再到模糊的标定板图像，如下为其中三幅图像：

中间为最清晰的图像。

采用五种评价函数，对一百多幅图像进行计算，并将结果进行归一化，得到如图所示结果：

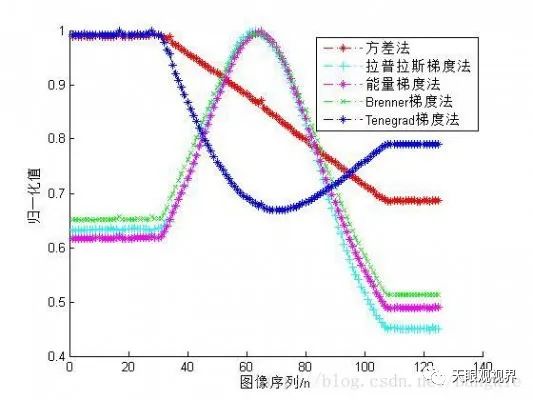
一个好的评价函数需要具有单峰性，无偏性，灵敏性，在本实例中，采用Laplace、能量梯度和Brenner梯度法较好，而方差法效果较差，Tenegrad梯度法反向了。

　　审核编辑：汤梓红