

先进的蓝牙角度估计技术增强了实时定位
描述
这些技术基于测量接收到的射频(RF)信号之间的相位差,并根据这些相位差对AoA或AoD进行数值计算。通过使用生成的角度读数,开发人员可以构建跟踪人员、移动设备和其他资产的系统,通常在室内环境中。这些新技术可以增强蓝牙信标应用程序的实用性和功能。天线阵列和AoA算法在正常运行的实时定位系统(RTLS)中发挥着重要作用。
定位技术有许多有用的应用,例如在全球范围内广泛使用的GPS。不幸的是,GPS在室内不能很好地工作,因此确实需要更好的室内定位技术。目标是使用外部跟踪系统跟踪单个对象的位置(或角度),或者让设备在室内环境中跟踪其自身位置。这种定位系统可以跟踪仓库中的资产或购物中心中的人员。
蓝牙 AoA 和 AoD 技术为室内定位建立了标准化框架。在这些技术中,定位的根本问题归结为解决RF信号的到达和离开角度。让我们来看看这些技术的基础知识和估计到达方向的理论。目前蓝牙 AoA/AoD 规范处于成熟状态,但尚未公开。
考虑一个具有多天线线性阵列的设备用于接收器,一个具有一个天线的设备用于发射器。假设无线电波作为平面波前端而不是球面传播,我们可以安全地从远处观察时假设。如果通过空气发送正弦波的发射器位于垂直于阵列线的法线上,则阵列的每个天线(信道)都将看到同一相位的输入信号(图1)。如果发射器不在正常线路上,则接收天线将看到信道之间的相位差。该相位差信息可用于计算到达角。
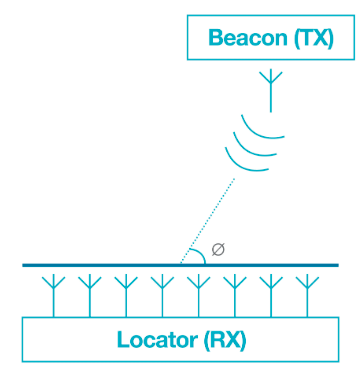
1.您可以找到带有多天线线性阵列的AoA用于接收器,以及带有一个天线的设备用于发射器。
实际上,接收器设备将需要多个ADC通道,或者使用RF开关从每个通道获取样本。它们被称为IQ样本,因为同相和正交相位读数的样本对是从相同的输入信号中获取的。这些样品在采样中具有90度的相位差。当此对被视为复数值时,每个值都包含相位和振幅信息,并且可以作为到达角估计算法的输入。
无线电波以光速(300,000公里/秒)传播。当使用2.4 GHz左右的频率时,相应的波长约为0.125 m。对于大多数估计算法,两个相邻天线之间的最大距离是半个波长。许多算法都需要这个;否则,我们会得到类似于混叠的效果。理论上没有最小距离限制,但在实践中,最小尺寸受到阵列的机械尺寸以及例如天线元件之间相互耦合的限制。
测量
测量AoD相位差的基本概念与AoA相同,但设备角色被交换。在AoD中,被跟踪的设备仅使用一根天线,发射器设备使用多个天线(如图2所示)。发射设备按顺序切换发射天线,接收端知道天线阵列配置和切换顺序。
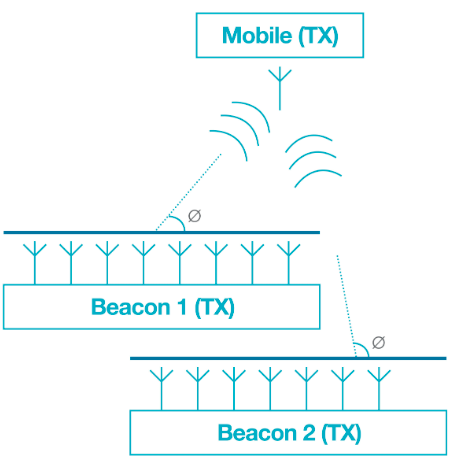
2. AoD 可以用单天线线性阵列确定接收器,使用具有多天线的设备来确定发射器。
从应用角度考虑这一点时,我们可以看到这两种技术之间的明显区别。在AoD中,接收设备可以使用来自多个信标的角度及其位置(通过三角测量)计算自己在空间中的位置。在 AoA 中,接收设备跟踪单个物体的到达角度。不过,请注意,可以执行这些技术的不同组合,因此它们不会限制在应用程序级别可以执行的操作。在蓝牙 AoA 和 AoD 中,与 AoA/AoD 相关的控制数据都通过传统的数据通道发送。通常,这些技术可以实现几度的角度精度和大约0.5米的定位精度,但这些数字取决于定位系统的实现。
设计挑战
最大且可能最明显的挑战之一是确定如何根据样本数据计算角度估计值。仅仅我们能够在理想环境中计算角度估计是不够的;我们还必须能够在信号高度相关或相干的具有非常重的多路径的环境中计算它们。相干信号是其他信号的延迟和缩放版本。例如,当无线电波从墙壁反射时,情况就是如此。
其他挑战包括信号极化。在大多数情况下,我们无法控制移动设备的极化,因此系统必须考虑这一点。此外,信号噪声、时钟抖动和信号传播延迟也会给问题增加自己的变量。根据系统规模,嵌入式系统的RAM,尤其是CPU要求可能很高。许多性能良好的角度估计算法都需要 CPU 提供大量的处理能力。
当我们介绍一些关于天线阵列和到达角估计的理论时,请注意AoD可以从AoA理论中推导出来。
到达角理论
角度估计方法和天线阵列对于定位系统正常工作至关重要。测向理论的历史可以追溯到100多年前,当时首次尝试解决这个问题时使用定向天线和纯模拟系统。许多年后,方法转移到数字世界,但基本原则保持不变。这些测向方法已经用于许多应用,例如医疗设备以及安全和军事设备。让我们考虑一下典型天线阵列和估计算法的基础知识。测向是指估计到达和离开角度的一般问题。
天线阵列
用于测向的天线阵列通常分为几类。最常见的是均匀线性阵列(ULA),均匀矩形阵列(URA)和均匀圆形阵列(UCA)。线性阵列是一维的,这意味着阵列中的所有天线都位于一条线上,而矩形和圆形阵列是二维的,这意味着天线分布在二维(在平面上)。使用一维数组,假设跟踪的设备在同一平面上一致地移动,则可以可靠地仅测量方位角。此外,使用二维阵列,可以可靠地测量3D半空间中的方位角和仰角。如果将阵列扩展到完整的3D阵列(天线分布在所有三个笛卡尔坐标上),我们可以测量完整的3D空间。
设计用于测向的天线阵列并非易事。当天线放置在阵列中时,它们开始影响彼此的响应;这称为相互耦合。请记住,在大多数情况下,我们无法控制发射端的极化。这给设计师带来了额外的挑战。在物联网应用中,这些设备通常被期望很小,甚至可以在非常高的频段工作。估计算法通常需要数组中的某些属性。例如,称为 ESPRIT 的估计算法基于数学假设,即数组被划分为两个相同的子数组。
角度估计算法
让我们看一下基于输入 IQ 数据估计到达角度的数学/算法问题。问题定义本身很简单——估计发射(窄带)信号到达接收阵列的到达角度。虽然问题陈述听起来微不足道,但针对此问题的强大而真实的解决方案并不容易,并且可能需要从硬件获得很大的处理能力。
制作音乐
接下来,我将介绍一种解决此问题的方法,一种称为多信号分类(MUSIC)的技术。虽然我不会检查任何定理的证明或此方法工作的原因,但我会给出该算法的高级视图,如图 3 所示。
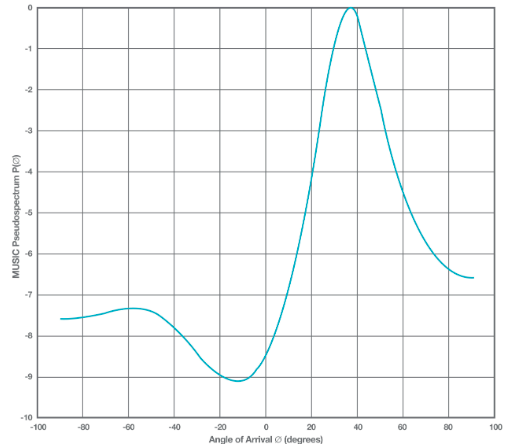
3.图中所示为峰值为36.5度的八天线ULA的音乐伪光谱。
让我们从均匀线性阵列的数学模型开始。我们得到了每个天线的IQ样本数据向量,我们称之为x。现在,每个天线(可以是0)看到相移加上一些噪声,在测量中,所以可以写成时间的函数:
x(t) = a(θ) s(t) + n(t) (1)
其中,信号通过空中发送,是天线阵列的转向矢量:
a(θ) = [1, ej2πdsin(θ)/λ, 。.., ej2π(m-1)dsin(θ)/λ(2)
其中相邻天线之间的距离,是信号的波长;是天线阵列中元件的数量,代表到达角度。
转向矢量(2)描述了由于与发射器的距离不同,每个天线上的信号是如何相移的。使用等式(1),我们可以近似于所谓的样本协方差矩阵,R断续器,通过计算
, (3)
其中 H 代表矩阵的埃尔米特转置。
样本协方差矩阵将用作估计算法的输入。MUSIC到达方向估计算法也称为子空间估计器。该算法在协方差矩阵上执行特征分解:
R断续器= V AV-1(4)
其中 是包含特征值和包含 R 的相应特征向量的对角矩阵断续器。
现在,假设我们试图估计一个带有天线线性阵列的发射器的到达角度。可以证明,任何一个的特征向量都属于所谓的噪声或信号子空间。如果特征值按升序排序,则相应的特征向量跨越噪声子空间,该子空间与信号子空间正交。根据正交性信息,我们可以计算出伪谱:
P:P(θ) = 1/aH(θ)节Ha(θ)(5)
最后一步是遍历 所需的值并找到 的最大峰值,该值对应于我们希望测量的到达角(参数)。
在理想情况下,MUSIC在良好的信噪比(SNR)环境中具有非常好的分辨率,并且非常准确。另一方面,当输入信号高度相关时,它的性能不是很好。在室内环境中尤其如此。多径效应会扭曲伪频谱,导致其在错误位置具有最大值。
空间平滑
空间平滑是一种解决由多路径引起的问题的方法(当存在相干信号时)。可以证明,通过使用原始协方差矩阵的子阵列计算平均协方差矩阵,可以“去相关”信号协方差矩阵。对于二维数组,可以按以下方式编写:
(6)
其中 和 分别是 x 和 y 方向上的子数组数,代表 :th 子数组协方差矩阵。
生成的协方差矩阵现在可以用作协方差矩阵的去相关版本,并馈送到 MUSIC 算法以产生正确的结果。空间平滑的缺点是它减小了协方差矩阵的大小,从而进一步降低了估计值的准确性。
请记住,蓝牙 AoA 和基于相位的 AoD 测向系统需要天线阵列、RF 开关(或多通道 ADC)和足够的处理能力来运行估计算法。设计适当的天线阵列和使用角度估计算法对于RTLS系统至关重要。RTLS设计人员还应该记住,高性能估计器算法通常对计算要求很高。
审核编辑:郭婷
-
蓝牙AOA定位的优势有哪些2025-01-21 1361
-
蓝牙信标人员定位系统原理及应用2024-08-21 2113
-
蓝牙AOA是如何实现人员定位的呢2024-08-06 971
-
为何自连采用蓝牙定位技术?2024-03-21 960
-
蓝牙AOA定位相较于蓝牙4.2的RSSI定位有哪些优势?2023-11-30 1404
-
仁微电子解答蓝牙AOA定位技术常见的问题2023-09-21 1515
-
蓝牙定位工牌胸牌|高精度定位|实时跟踪2023-09-08 1499
-
如何增强蓝牙接收信号强度,实现精准定位?2019-09-18 22605
-
设计技术增强了开关组件中的隔离2019-05-30 1368
-
蓝牙定位技术的应用2019-02-12 8700
-
UWB、RFID、蓝牙、WiFi定位技术比较2018-10-25 7334
-
声源定位中的时延估计方法研究2010-04-22 3830
全部0条评论

快来发表一下你的评论吧 !

