基于自适应粒子群算法优化支持向量机的负荷预测

作者：廖庆陵，窦震海，孙 锴，朱亚玲    

引 言

随着现代工业的不断发展，电力已经深入人们的生产和生活中，负荷预测则是保证电力系统稳定运行的关键技术。电力负荷数据是随机非平稳序列，几乎不可能达到完全准确，因此提升预测精度是学者们共同追求的目标[1⁃2]。传统预测方法在短期预测上受各种条件影响，在不同地区、不同情况下表现出来的适应性相较于新的智能预测算法有较大差距。新兴的智能预测算法相对于传统预测方法已经有了较好的效果，这方面的算法也越来越多，基于极限学习机、随机森林、神经网络等常见算法的优化改良较多。

通常使用其他算法与智能算法相结合的模式，这种模式能结合两种算法的优势，带来较好的优化效果，缺点是可能会导致训练时间变长[6]。文献[7]采用基于双种群的粒子群算法（DP⁃PSO）寻求混合核函数LS⁃SV模型的最优参数进行日平均负荷预测，由于粒子群算法相对容易陷入局部最优，得到最佳参数设定的成功率得不到保障，从而影响预测结果。本文吸取其他算法的先进经验，同时针对粒子群算法的不足，提出一种改进自适应粒子群算法优化支持向量机模型的负荷预测。首先选用支持向量机为负荷预测的工具，支持向量机是在分类与回归分析中分析数据的监督式学习算法，因为其对于负荷预测有着很好的效果和实用性，常被应用到负荷预测中。但支持向量机的问题是使用时需要将参数 c和 g 调到合适的值才能达到最好的预测分类效果，所以在使用过程中常常会用到各种群体智能算法对支持向量机参数进行调优。

1 算法原理及改进

1.1 群体算法

大多群体算法都有一个共同的缺点，参数在程序运行之前就一次性设置完成，不再变动，使得群体算法在运行前期或后期难以达到最好的优化效果。比如粒子群算法中，固定的位置更新公式在运行的后期往往不能达到最优的运行效果。针对群体算法位置更新公式的问题，部分改进算法会用到根据迭代数进行调整的位置更新公式，比如带有惯性因子的粒子群算法，在迭代时对惯性因子进行线性递减的操作，这样惯性因子随着迭代次数逐渐下降，使得在算法运行的后期粒子群的局部搜索能力得到提高。这种方法的效果要好于固定惯性因子。

但是这种根据迭代数线性减少的方式并没有考虑到每个个体以及种群的实际状态，如果前期的搜索并非很有成效，这时贸然减小粒子群算法中的惯性因子会使得搜索效率降低甚至陷入局部最优无法跳出。针对群体算法的参数调整或根据实际运行状态动态调整的问题，本文提出一种自适应动态因子。将适应度函数算出的适应度值作为算法运行状态的判断依据，根据每一代种群适应度值的变化来动态调整参数，以适应各种群体算法的实际运行状态。

自适应动态因子更新公式如下：

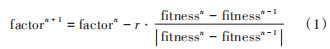
1.2 粒子群算法原理

粒子群算法是一种在生物种群行为特性中得到启发的求解优化问题的算法。粒子群算法首先初始化一群随机粒子，然后迭代找到最优解，在迭代过程中，粒子通过跟踪极值加上更新公式来更新位置。算法流程如下：

1）初始化：首先设置最大迭代次数、目标函数的自变量个数、粒子的最大速度，在速度区间和搜索空间上随机初始化速度和位置，设置粒子群规模，每个粒子随机初始化。

2）根据适应度函数计算每个粒子的适应度，得到个体极值与全局最优解。3）通过式（2）、式（3）更新速度和位置。

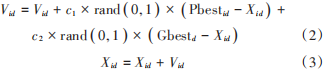
式中：Vid 是粒子 i 在第 d 维度的速度；c1 和 c2 为加速常数；rand ( 0, 1 ) 是值为大于 0 且小于 1 的随机数；Pbestid是粒子 i在第 d维度的最好位置；Gbestd是全部粒子在第d维度的最好位置。

4）达到设定的迭代次数。

和其他群体智能算法一样，粒子群算法在优化过程中，种群的多样性和算法的收敛速度之间始终存在着矛盾。对标准粒子群算法的改进，无论是参数的选取或是其他技术与粒子群的融合，其目的都是希望在加强算法局部搜索能力的同时保持种群的多样性，防止算法在快速收敛的同时不容易出现早熟。

1.3 粒子群算法的改进

1.3.1 混沌初始化

种群初始化对于粒子群算法的求解精度和收敛速度有着较大的影响。粒子群算法的第一步初始化：传统粒子群算法一般采用随机初始化来确定初始种群的位置分布，由计算机生成随机数，再根据式（4）随机生成各个粒子的初始位置。通常这种随机初始化能生成每次不一样的初始种群，使用起来比较方便。但也存在弊端，就是初始粒子在解空间的分布并不均匀，常常遇到局部区域的粒子过于密集，同时一部分区域的初始粒子却过于稀疏。这样的情况对优化算法的前期收敛是非常不利的，对于容易陷入局部最优的群体优化算法，可能导致收敛速度下降甚至无法收敛的情况发生。

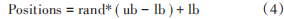
式中：Positions 代表生成的粒子位置；rand 代表生成的随机数，取值范围为[0，1]；ub，lb 分别为解空间的上下界。

而混沌初始化则可以有效地避免这些问题。混沌初始化具有随机性、遍历性和规律性的特点，是在一定范围内按照自身规律不重复地遍历搜索空间，这样生成的初始种群在求解精度和收敛速度方面有着明显改进。本文中的混沌初始化选用 TentMap 混沌模型，其公式如下：

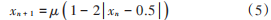
式中：μ ∈ ( 0, 4 ]，为混沌模型的映射参数，本文中 μ 的取值为 1，使混沌系统处于完全混沌状态；xn是由混沌系统生成的混沌数字；x0为初始值，本文中取值为 0.588。

1.3.2 动态自适应惯性因子

原始的粒子群算法中是不含有惯性因子的，但是使用效果不够好，所以在使用过程中，普遍使用的是带有惯性因子的粒子群算法。比较常见的惯性因子有：常数惯性因子、线性下降惯性因子和模糊惯性因子。算法在搜索最优点时，全局搜索能力与局部搜索能力不能顾此失彼。惯性因子 ω 就能在一定程度上起到平衡的作用，增大 ω 可以加强全局探测能力，而减小 ω 则能加强局部搜索能力。带有惯性权重的粒子速度更新公式为：

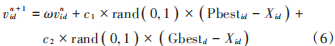
式中 ω是惯性因子，为一个非负数。常数惯性因子粒子群算法相较于原始粒子群算法在使用效果上有较大优势，能调节粒子群的全局搜索能力或者局部搜索能力，但是常数惯性因子并不能同时兼顾，于是又有学者提出一种随着迭代次数的增加线性降低惯性因子的方法。线性下降惯性因子的计算公式如下：

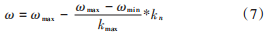
式中：ωmax 和 ωmin 分别是惯性因子的最大和最小值；kn 为当前迭代数；kmax是最大迭代数。

线性下降惯性因子的粒子群算法在开始时惯性较大，适合大面积的搜索，能快速找到最优解的大致位置，之后随着 ω 逐渐减小，粒子惯性减弱，加强局部搜索能力，能更精确地搜寻最优解。这种方法相较于常数惯性因子粒子群算法有较大的提升，但是因为不管是否适应度变得更好，惯性因子都会以同样的速度下降，所以线性下降惯性因子粒子群算法有时也会出现寻优效果差的问题。本文吸取前人改进算法的优点，提出一种动态自适应惯性因子。每次迭代更新所有粒子的位置后计算所有粒子的适应度，如果种群适应度比上一代种群适应度更好，那么调小惯性因子 ω，粒子群的局部搜索能力就会得到提高。相反，如果种群适应度降低，就调大惯性因子 ω，粒子群的局部搜索能力就会得到减弱，全局搜索性能得到提升。动态自适应 ω的计算公式如下：

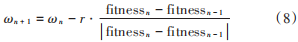
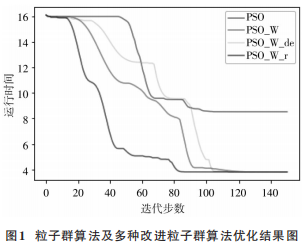
式中：fitnessn为周期n时的最优适应度值；ωn为周期n时ω的 值 ，ω的取值范围是 [0.4,0.9],初始值设置为0.75；r为增益倍数，取值范围是[0.02,0.05]。用经典粒子群优化（PSO）算法、惯性粒子群优化（PSO_W）算 法、线性下降惯性因子粒子群优化（PSO_W_de）算法和自适应动态粒子群优化（PSO_W_r）算法对函数进行寻优，运行结果如图 1 所示。可以从图中看出，通过自适应惯性因子改进的粒子群算法在效率上远远高于其他几种粒子群算法。

1.3.3 差分变异算子

粒子群优化算法虽然有运行速度快的优点，但是不可避免地容易陷入局部最优。本文将差分算法中的差分变异算子引入粒子群算法中：在每次迭代完成之后，选取适应度最差的30%~50% 的粒子进行变异操作。这样可以在加快寻优速度的同时，防止算法陷入早熟。变异公式如下：

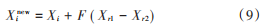
式中：Xi 为变异前的粒子 i；Xinew 为变异后的粒子 i；F 为缩放比例因子，通常取值为 0.5。

2 自适应粒子群算法优化支持向量机模型

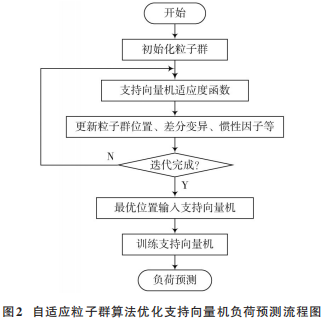
支持向量机中有两个重要参数c和g。其中：c 是惩罚系数，是对误差的宽容度，c越高越容易过拟合，c过小则容易欠拟合；g 是 RBF 内核中的一个参数，g 值越大，支持向量越少，g 值越小，支持向量越多。支持向量的个数影响训练与预测的速度。因此在支持向量机的使用中，参数的优化会带来更好的效果。本文选择粒子群优化算法以及自适应粒子群优化算法对支持向量机的参数 c 和 g 进行调优，使得负荷预测模型能有更好的预测效果。用自适应粒子群算法优化支持向量机参数进行负荷预测的具体实现步骤如下：

1）混沌初始化粒子群的初始位置，每个位置的坐标值代表支持向量机参数c和 g。

2）计算出每个粒子对应的适应度，适应度函数选用支持向量机模型里的适应度函数。

3）再根据自适应粒子群算法的位置更新公式进行移动，同时根据适应度值的变化，动态调整惯性因子 ω。

4）将适应度较差的一部分粒子进行差分变异。并且重新回到步骤 2），直到达到迭代次数。

5）将适应度最好的粒子的位置参数取出，作为支持向量机的参数c和g。

6）用训练数据对当前支持向量机进行训练。

7）用训练好的支持向量机模型进行负荷预测，输出结果。

自适应粒子群算法优化支持向量机模型简要流程图如图2所示。

本文用粒子群算法优化的支持向量机和改进的自适应粒子群算法优化的支持向量机进行负荷预测，并将结果进行对比分析。两种算法都采用相同的数据、相同的输入输出量。本文采用美国某地区2019年8—9月的历史负荷值作为实验数据，共 1 464 个每小时一次的负荷数据，输出量为一天中每个小时的负荷预测值，输入量为预测点当天前一个和前两个小时的负荷值，前一天同一小时、前一小时、后一小时负荷值，前一周同一小时、前一小时、后一小时负荷数据。对输入数据需要进行归一化预处理，以提高算法运行效率以及预测精度。预处理方法是用线性转化的方式将数据成比例地转化到[0，1]区间内。这样将数据限定在一个较小范围，预处理公式如下：

式中：x 是原始数据；x′是处理后的数据；xmax 和 xmin 分别为输入样本集的最大值和最小值。粒子群算法种群规模取 40，增益倍数 r 取 10，迭代次数 Kmax 取 100。预测结果如图 3所示。

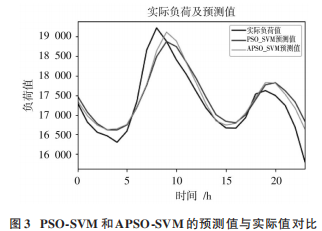
根据实例数据，利用式（11）分析可以得出：在迭代次数为 100 次的情况下，改进自适应粒子群算法优化的支持向量机预测值的 MAPE 值为 1.569%；原始粒子群算法在同样迭代次数的情况下误差相对较大，MAPE 值为 2.248%。

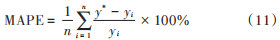
式中：y ∗为预测值；yi为实际值；n为样本量。

3 结 语

传统的粒子群优化算法的惯性因子为固定值，导致前期或后期效率较低。自适应惯性因子使得粒子群的惯性因子在算法运行过程中根据适应度自动调整，以达到提升搜索效率的目的，同时针对粒子群算法容易陷入局部最优的问题提出加入差分变异算法，对适应度差的粒子进行差分变异，并用改进后的自适应粒子群算法优化支持向量机参数 c 和 g，得到一种自适应粒子群算法优化的支持向量机模型，使得支持向量机与粒子群优化算法能很好地配合进行负荷预测。自适应粒子群算法可以使得这个优化过程相对于原始粒子群算法更加高效，这主要得益于改进的自适应惯性因子相较于传统的固定惯性因子，同时增强了前期的全局搜索能力和后期局部搜索能力，从而更快速寻找到更优的支持向量机参数。根据实际数据进行实验，对比本文提出的模型与未经优化的模型，发现预测精度有明显提升。

尽管如此，本文方法仍有改进空间。以后的工作可以从以下两方面着手：需对粒子群算法的智能搜索策略、惯性因子、学习因子和其他重要参数的取值进行更加深入的分析，继续挖掘粒子群算法的寻优潜力；将APSO⁃SVM 算法运用于更多的领域，提升改进算法的应用范围，使其具有更好的推广价值。

审核编辑：郭婷