

纯电感或纯电容性的负载在交流电源的功率消耗
电源/新能源
描述
上篇文章中,我们说明了在交流电路中,电容和电感的电压波形与电流波形,并说明了「容抗」与「感抗」的公式。由于电容电感在交流电路中都会造成电压与电流的相位差,因此最大的电压与最大的电流并非同时发生,但我们仍然可以套用奥姆定律来计算最大的电流。
这一回我们继续来解释阻抗的观念,以及用来表达它的数学工具。
能量的流动
上一回我们提到,在交流电路中,如果负载是电感或电容,电流与电压之间会产生相位差。
以电容为例,如果一个交流电源的负载是电容器,那么电容器上的电流波形就会「超前」电压波形,也就是在每一个交流电源的正弦周期中,电流都会比电压先上升到最大值。
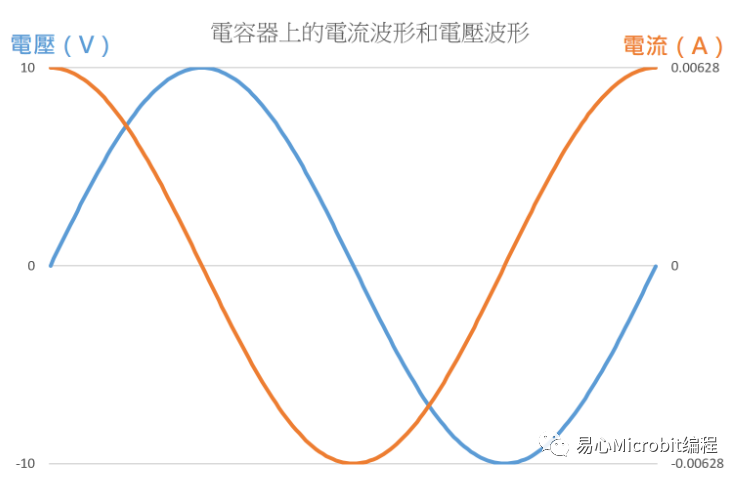
由于这是一个交流系统,它的电压有正有负,电流方向也有正有负。如果负载是一个电阻,就如我们上一回的第一个例子,它在电阻上面建立的电压和电流是没有时间差的。电压是正的,电流也就是正的;电压是负的,电流也就是负的。
但如果负载是电容或电感的时候,负载上的电流和电感就会有时间差了。这个时间差会导致电压和电流的正负号并非时时都一致。
以上面那图为例,我们可以把电容上的电压波形和电流波形的符号画出来:
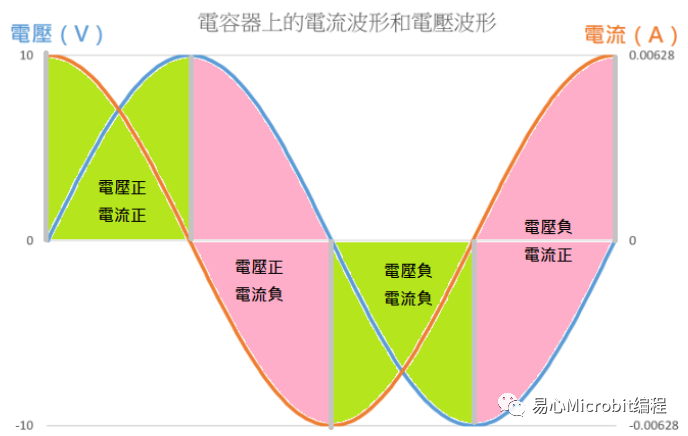
可以发现,因为两者都会在正负之间变换,而且变换的周期有时间差,所以会有电压正/电流正、电压正/电流负、电压负/电流正、以及电压负/电流这四个不同的组合。
根据功率的定义,功率是电压乘上电流:P = I * V。
我们把上面那张图的蓝色电压曲线和红色电流曲线逐点相乘,就可以得到功率的曲线:
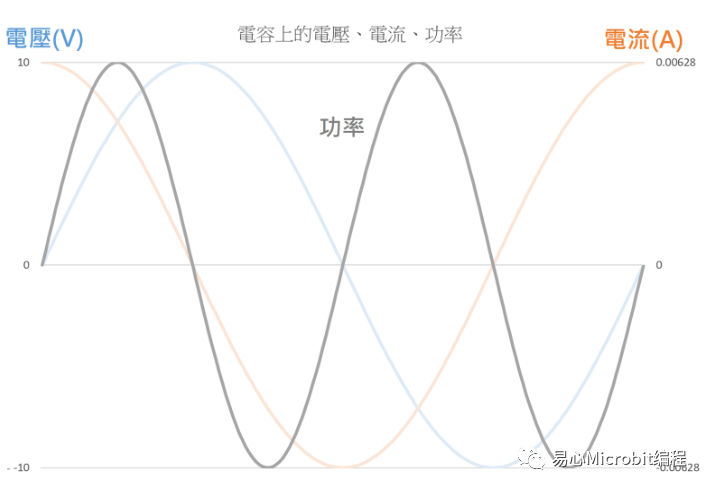
功率和电压、电流一样,也有正负号,因此乘出来的曲线也有正有负。当电压和电流的符号相同时,功率为正。当电压和电流的符号不同时,功率为负。
有趣的事来了。功率的符号代表的是能量流动的方向。如果我们定义功率为正时,是能量流入电容器,那么当功率为负时,就是能量从电容器流出。流出?流到哪里去?流回电源。
就算不用微积分认真算,其实从功率的曲线我们也可以看出来,功率为正的面积应该等于功率为负的面积;换句话说,这些从电源流入电容器的能量,在下一个周期又从电容流回电源。
换句话说,如果我们在交流电源上面接一个电容器当负载,其实它不会消耗能量,它会储存能量一小段时间之后,再把能量送回电源去,周而复始。
聪明的读者此时可能也想到了,在交流电源上面接电感当负载,也会是类似的状况。对,电感一样会造成电流和电压有时间差,但不同的是,电感上的电流会落后于电压,刚好跟电容相反。
我们一样可以把电感上的功率曲线画出来,得到类似的结果。
因此这里有一个很重要的结论:纯电感或纯电容性的负载,在交流电源之下是不消耗功率的。
阻抗的符号系统
由于电容和电感在交流电路中会造成电流和电压的相位差,而且它们造成的效应刚好相反:一个会让电压落后电流,另一个则会让电流落后电压,因此两者的效应是可以互相抵消的。换句话说,如果我们串联电感与电容在交流电路上,两者的效应可以互相消长,至于谁消谁长,就要用一个比较复杂的符号系统来计算了。
我们上周说过,电容容抗的公式是:XC= 1 / 2
编辑:黄飞
-
可编程交流电源的特点及应用2023-11-09 1521
-
如何区分交流电容、电阻和电感负载2023-04-23 2699
-
交流电源的原理和应用范围2022-01-06 2167
-
全天科技交流电源2021-12-31 642
-
全天科技交流电源产品基本功能介绍2021-12-11 634
-
怎样去计算纯电容交流电路中的无功功率2021-09-24 5695
-
交流电源和直流电源有什么不同2021-05-24 10984
-
电源技术之交流电路中无源器件2020-09-24 2673
-
电源技术之交流电容和电容电抗(一)2020-09-16 4976
-
交流电源输出直流电压的纹波和滤波电容、负载大小的关系2019-12-25 10231
-
感性与容性负载的区别及无功功率补偿2019-05-22 6868
-
交流电源负载箱2018-11-29 4635
-
纯电感电路有功功率和无功功率2018-02-27 59997
-
一文读懂纯电阻电路和纯电感电路2017-11-02 17158
全部0条评论

快来发表一下你的评论吧 !

