支持向量回归机在风电系统桨距角预测中的应用

　　支持向量机(Support Vector Machines，SVM)是根据统计学理论中最小化原则提出来的，由有限数据得到的判别函数，对独立的测试样本能够得到较小的误差，包括支持向量分类机 (Support Vector Classification，SVC)和支持向量回归机(Support Vector Regression，SVR)。此文用的就是SVR算法，其目的是构造一个回归估计函数，将非线性函数的回归估计问题转化为一个具有线性等式约束和线性不等式约束的二次规划问题。可以得到唯一的全局最优解。此最优解，在预测桨距角中就是最佳桨距角。

　　1 SVR

　　1.1 SVR的引入

　　现有的预测桨距角算法有基于BP算法和基于LV算法的神经网络，BP算法收敛速度慢、精度低，LV算法泛化能力差，因此，能改变现有算法不足的支持向量机算法应运而生。SVM方法最早是针对模式识别问题提出的，随着对ε不敏感损失函数的引入，现已推广应用到非线性回归估计和曲线拟合中，得到了用于曲线拟合的回归型支持向量机SVR，表现出很好的学习效果。

　　1.2 回归算法原理

　　标准的SVR算法，分为线性和非线性两种。SVR的基本思想是：将输入样本空间非线性变换到另一个特征空间，在这个特征空间构造回归估计数，这种非线性变换是通过定义适当的核函数K(xi，xj)来实现的。其中K(xi，xj)=φ(xi)·φ(xj)，φ(x)为某一非线性函数。

　　假设给定了训练数据，{(xi，yi)，i=1，2，...，n}，xi为学习样本，yi为对应的目标值。定义线性ε不敏感损失函数为：

　　

 

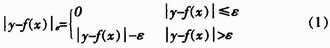
　　即如果目标y值和经过学习构造的回归估计函数f(x)的值之间的差别小于ε，则损失等于0。

　　假设非线性情形的回归估计函数为：

　　

 

　　要寻找w、b对，使在式(1)不变的前提下最小化

。

 

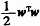
　　同时考虑到当约束条件不可实现时将松弛变量

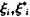
引入，这样最优化问题为：

 

　　

 

　　利用拉格朗日乘子法来求解这个约束最优化问题，因此构造拉格朗日函数

　　

 

　　其中NNSV为标准支持向量数量。由式(7)和式(8)知，尽管通过非线性函数将样本数据映射到具有高维甚至无穷维的特征空间，但在计算回归估计函数时并不需要显式计算该非线性函数，而只需计算核函数，从而避免高维特征空间引起维数灾难问题。

　　2 桨距角预测与Matlab仿真

　　2.1 样本的获取与预处理

　　要使风速改变时，桨距角随之改变的值为最佳桨距角，就要选择合适的学习样本，用来训练和检验。由于自然界风速处于不断变化中，较短时间3～4 s内的风速上升或下降总是不断发生，因此变桨距机构也在不断动作，在转子电流控制器的作用下，将桨距角的实际变化情况选做样本。共选取128组样本数据，其中学习样本80个，用来检验的预测样本48个。选择的训练样本和测试样本形式如下表1所示。

　　

 

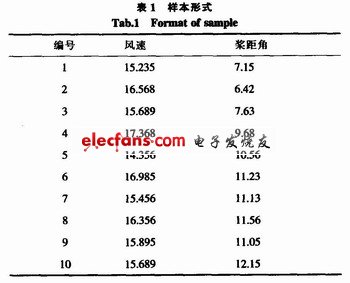
　　并将此样本存为.txt格式，以便于在Matlab仿真时的数据输入。

　　2.2 SVR函数的参数选择

　　2.2.1 SVR函数

　　该函数根据训练样本设计出最优回归函数，并找出支持向量。该函数有6个参数，分别是训练样本的输入、训练样本的输出、核函数、惩罚因子、损失函数和不敏感系数。输出参数为支持向量个数、拉格朗日乘子及偏置量。即

　　[nsv，beta，bias]=svr(X，Y，ker，C，loss，ε);

　　X——训练样本的输入，在本文中就是样本中用于学习和检验的风速值。

　　Y——训练样本的输出。就是样本中对应的桨距角。

　　ker——核函数，要使误差小需选择适当的核函数，这里选择的是rbf核函数。

　　C——惩罚因子，C取的过小，训练误差变大，系统的泛化能力变差，C取的过大，也会导致系统的泛化能力变差。

　　loss——损失函数。

　　ε——不敏感系数，ε取的小，回归估计精度高，但支持向量数增多，ε取的大，回归估计精度降低，但支持向量数少。

　　nsv——支持向量的个数。

　　beta——拉格朗日乘子。

　　Bias——偏置量。2.2.2 输出函数SVRoutput

　　该函数利用svr函数得到的最优回归函数来计算测试样本的输出，并返回。

　　2.2.3 svrplot

　　该函数用来绘制出最优回归函数曲线，并标识出支持向量。

　　2.2.4 svrerror

　　该函数用来显示根据最优回归函数计算的测试样本的拟合误差。

　　2.2.5 核函数的选择

　　常用的核函数有4种：线性核函数(linear)、多项式核函数(polynomial)、径向基核函数(RBF)和Sigmoid核函数。在一般情况下，首先考虑的是RBF，主要基于以下原因：1)RBF可以将样本映射到一个更高维的空间，可以处理类别标签和特征之间的关系是非线性时的样本。2)与多项式核函数相比，RBF需要确定的参数要少，核函数参数的多少直接影响模型的复杂度。3)对某些参数，RBF与sigmoid核函数具有相似的性能。

　　衡量SVR的最小误差和泛化能力准则，并优化该准则，本文选择了RBF核函数。

　　2.3 Matlab仿真

　　2.3.1回归拟合

　　在Matlab编程实现函数的回归拟合，并检验数据。主函数程序段如下：

　　

 

　　2.3.2 函数回归拟合并检验的仿真结果

　　应用Matlab支持向量机工具箱编程实现系统的学习训练过程，由80个学习样本训练而得到的函数拟合结果如下图1所示。

　　

 

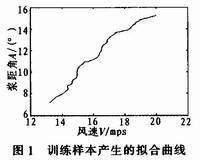
　　利用训练好的神经网络模型可以对桨距角进行预测，只要输入即时风速，就可确定出相应桨距角大小。之前利用BP算法的均方误差为0.290 3，LM算法的均方误差为0.278 1。图2为由SVR算法对48个样本值检验的结果。可知，预测值与实际桨距角值基本一致。拟合误差err=0.175 6。

　　

 

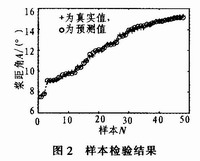
　　3 结束语

　　文中介绍了支持向量机的回归算法理论，用SVR算法代替之前的BP算法和LV算法，研究了风力发电系统中随风速变化桨距角的值，由函数拟合理论对桨距角进行了预测并检验，由于支持向量机采用结构最小化原则代替经验经验最小化原则，采用适当的核函数，同比其他算法使拟合误差达到了最小，大大提高了变桨距系统的精度和效率。将该算法应用于DSP芯片上稍作改进，加上外围电路的设计，即可应用在风电系统的控制领域。