考虑柔性负荷的微电网快速一致性多目标调度

作者：邵雪莲，陈珍萍，付保川，吴征天

引 言

随着分布式能源的大量涌现，微电网作为接纳众多分布式电源的有效方式，受到了广泛关注。然而，微电网在面对分布式电力元件接入时存在着一些弊端，例如环境污染较为严重、经济效益不高、难以灵活应对柔性负荷的即插即用、系统的稳定性受机组的变化影响较大等。

经济调度指在满足一定的系统约束前提下，通过合理安排发电使系统运行的经济性尽可能地提高。国内外关于微电网的经济运行与优化调度的研究一直处于有增无减的趋势。经济调度算法基本分为两类：集中式算法（如λ迭代法、生物遗传算法、免疫粒子群算法等）和分布式算法（如基于复制因子的算法、一致性算法、交替乘子算法等）。现有的经济调度大多是仅仅考虑了发电成本最小的单目标优化问题，无法满足微电网多元件参与与节能减排的发展趋势。

为了实现微电网的多目标优化调度运行，文献[11]研究了在时延和噪声等通信环境下兼顾经济和环境的多目标调度模型，在一致性算法中额外引入了虚拟一致性变量，避免了不理想通信环境带来的影响，但是未考虑储能装置和柔性负荷的协调作用，并且其目标函数只涉及到了发电机，没有考虑其他电力元件的出力调度。文献[5]针对电热综合能源系统研究了计及网络传输损耗的电热综合能源系统多目标优化调度模型，该模型同时考虑电传输损耗和热传输损耗，采用了基于双层双 λ的迭代算法以最小化系统经济环境调度目标，但属于集中式控制。文献[12]针对电转气设备接入综合能源系统时，用户的行为会影响电、热负荷比例的问题，建立了考虑用户需求响应的兼顾电⁃气⁃热的两阶段日前综合能源系统经济调度模型，不仅促进了清洁能源的利用率，还提高了系统的经济性，但是未考虑系统的传输损耗。

微电网信息通信网络和电力物理网络在未来的联合会越来越紧密，因而可以考虑借助多智能体系统一致性算法，充分利用双方渗透的便利实现多目标优化调度。在实际的应用中，一致性协议好坏的性能指标和系统的稳定性均与算法的收敛速度有关。同时，由于可再生能源易受环境影响，用电负荷也不规律变动，导致微电网的调度需求十分频繁，因此要求一致性协议有较高的计算速度。

基于现有研究，本文将快速一致性算法引入含柔性负荷的微电网环境经济多目标调度中。首先，建立一种综合考虑污染气体排放、传统发电机发电成本、储能成本、柔性负荷用电效益及网络损耗的微电网多目标优化模型；其次，应用线性加权法将多目标优化问题转化为单目标优化问题；再次，采用引入反馈增益的分布式快速一致性算法和拉格朗日乘子法求解该优化模型；最后，基于改进的IEEE 14节点系统，通过3个算例验证了所提方法的有效性。

1、理论基础

1.1 分布式调度

传统的电力调度往往采用集中式方法，此方法对调度中心的要求和依赖性较高，一旦故障易导致整个控制系统瘫痪，并且各节点与中心的通信建设与维护成本较高，另外系统难以应对频繁的时变拓扑。

与集中式方法相比，分布式调度可以在每个智能体中同时进行一致性变量的迭代计算。领导者负责系统功率平衡的集中调整，确保所有智能体在迭代计算后能收敛。因而分布式方法有较大的灵活性和可扩展性。

1.2 快速一致性算法

本文用有向图G表示微电网中节点间的通信关系。邻接矩阵A=(apq)n×n用来描述节点p, q之间的通信关系，其中，n表示节点数。节点p能够获取节点q的状态信息时，apq=1；当节点p无法获取节点q的信息或当p=q时，apq=0。定义节点 p 的邻居集合为Np；图G的入度矩阵为D=diag（dpp），其中dpp=∑p≠qapq。

多智能体系统一致性算法发展至今已有多种形式，其中，一阶离散一致性算法得到了较为广泛的应用，可以表示为：

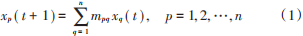
式中：xp (t)是第p个智能体的状态，t为迭代序列；mpq 为行随机矩阵的第(p, q )个元素。

一致性算法式（1）常见于无向通信电网经济调度中，为区别起见，本文将式（1）记为传统一致性算法。为提高有向通信微电网多目标调度的收敛速度，本文选用基于局部信息反馈的单增益快速一致性算法[13]：

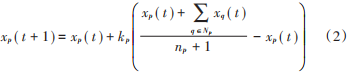
式中：kp > 0 ( p = 1, 2,⋯, n )为智能体 p的反馈增益；np为智能体 p 的邻居智能体数量，也即智能体 p 的入度，且有np=dpp。

2、基于快速一致性的多目标调度

2.1 多目标模型

本文研究的微电网处于独立运行方式，采用的优化策略是：同时考虑经济和环境两个目标，通过优化控制燃料发电机、储能蓄电池和柔性负荷等可控电力元件的有功功率，最小化微电网的运行成本和污染物排放综合总目标。

2.1.1 环境调度

环境调度指在最小化系统中传统燃料发电机的污染气体排放量。环境调度的目标函数具体描述为：

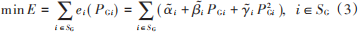
式中：αi, βi, γi为第i台机组的排放系数；PGi为第i个发电机组的输出功率；SG为发电机单元集合；ei ( PGi )为第 i个发电机组的污染气体排放量，可以按一定规则换算成费用[11]。

2.1.2 经济调度

本文将柔性负荷考虑进经济调度目标，符合微电网社会效益最大的现实需求。经济调度涉及储能蓄电池成本、传统燃料发电机的有功发电成本和柔性负荷的用电效益。

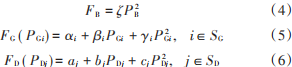
式中：ζ表示蓄电池储能成本的参数；αi, βi, γi分别为第i个发电单元成本的参数；aj, bj,cj 分别为第 j 个柔性负荷用电效益的参数；PGi 为第 i 个发电机组的输出功率；PDj 为第 j个柔性负荷的功率；SG为发电机单元集合；SD为柔性负载单元集合。

那么经济调度目标为：

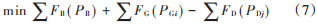
2.1.3 综合环境与经济的多目标模型

微电网中有功传输损耗通常占总负荷功率的3%~7%，因而将传输损耗考虑进系统功率平衡非常重要。假定传输损耗与负荷的关系是线性的[14]，用传输损耗因子sr表示传输损耗 PL：

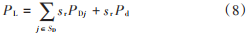
在微电网多目标调度过程中，需满足有功功率平衡约束。用ΔP表示系统总有功功率差，则有：

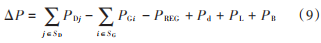
式中：PREG表示可再生能源机组功率；Pd表示系统纯负荷总功率；PB表示储能电池的功率。

为了同时处理环境与经济两个目标，采用线性加权法将多目标问题转化为单目标问题，兼顾到功率平衡，那么综合环境与经济的多目标模型可表述如下：

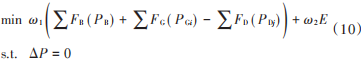
式中ω1+ω2=1且0<ω1 ,ω2<1。

2.2 基于快速一致性的调度方法

对于最小化问题式（10），利用拉格朗日乘子法将等式约束问题转化为如下无约束问题：

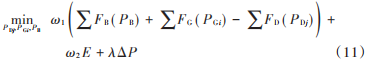
式中 λ表示与等式约束对应的拉格朗日乘子。对式（11）中变量 PDj，PGi，PB 和 λ 分别求偏导并求解其方程组，可得系统多目标调度模型最优解为：

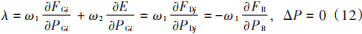
综合式(3)~式(6)和式(12)，可求得对应的发电机、柔性负荷、储能蓄电池的 λ分别为：

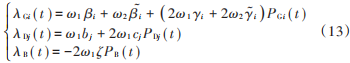
基于上述分析，可选择λ为该一致性算法的一致性变量，通过与邻居交换信息更新其一致性变量，最终使得网络中所有智能体的一致性变量收敛于统一值，也即λGi = λDj = λB，实现了系统的最优调度目标式（12）。假设微电网中每个发电机、柔性负荷和储能蓄电池都已嵌入了一个本地智能体，将其记为智能体p。根据式（2），系统发电机、柔性负荷和储能蓄电池的λ快速一致性算法可写为：

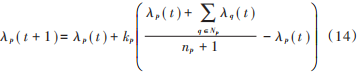
在一致性迭代过程中，为保证系统的功率平衡，需选择一个“决策主节点”，即“领导节点”。“领导节点”通过获取系统的整体功率偏差不断调节自身一致性变量，通过信息交换促使其他节点的一致性变量实现实时调整。对于领导节点，其更新公式为：

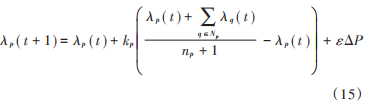
式中：ε为功率平衡调节系数，与“领导节点”的收敛速度有关，一般设为正标量。

本文将系统的功率偏差作为判断收敛的条件，即当|ΔP≤δ|，认为该一致性算法达到了收敛，其中δ为一个阈值，取值一般很小。

在实际的微电网中，考虑到发电机组、柔性负荷和储能蓄电池的有功功率都为受限值，可用下述不等式表示：

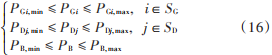
式中：PGi, max与PGi, min为第 i个发电机的出力上下限；PDi, max和 PDi, min为第 i个柔性负荷的出力上下限；PB, max和PB, min为储能蓄电池功率的上下限。

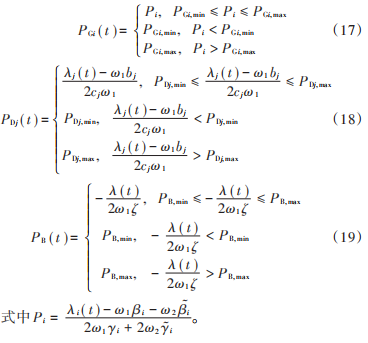
综合式（13）和式（16）可得，传统发电机、柔性负荷和储能蓄电池有功功率迭代分别为：

基于快速一致性的调度算法步骤如下：

Step1：输入各节点的初始功率值，得到各节点一致性变量的初值 λp ( 0 )和系统初始功率差 ΔP(0)；

Step2：微电网中跟随节点和“领导节点”分别按照一致性迭代式（14）和式（15）计算 λp (t)；

Step3：根据更新后的λp (t)，网络发电机节点、柔性负荷节点和储能节点分别按照式（17）、式（18）和式（19）计算 PGi (t)，PDj (t)和PB (t)；

Step4:"领导节点"根据 PGi (t),PDj(t)PB(t)的计算值,按照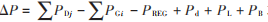求系统ΔP(t)，并判断|ΔP(t)|≤δ是否满足，若满足，则迭代结束，系统多目标调度达到最优；否则，跳转至 Step2继续进行迭代和功率调整。

3、仿真结果与分析

基于改进的IEEE 14系统图进行仿真以验证本文所提策略的有效性。系统通信网络的有向拓扑如图1所示。节点1~节点4分别表示发电机G1~G4，节点 5~节点 7 分别表示柔性负荷D1~D3，节点8表示储能蓄电池B。

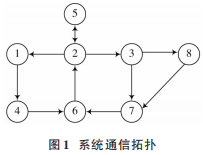
3.1 系统参数设置

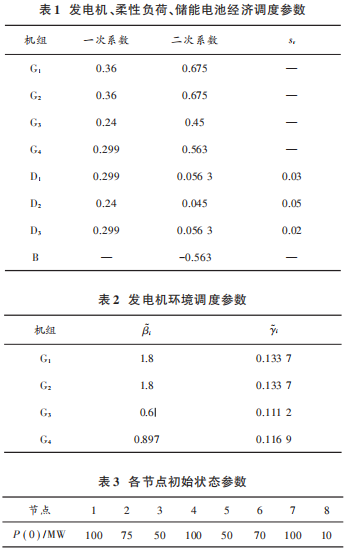
考虑到系统的收敛性和最优调度结果不受传统发电机参数αi，αi 和柔性负荷参数aj的影响，设定αi=αi=aj=0。由于系统中存在储能设备，可再生能源发电机在一定时间内可以维持其功率恒定，设置可再生能源输出功率PREG=300 MW 不变。系统的基础纯负荷设为400MW。设置ω1=0.25,ω2=0.75 ，判 定 系 数δ=0.001。微电网电力单元相关参数及发电约束参数如表1~表3所示。在调度过程中将G2和D2设为“领导节点”。假设所有可控机组的功率范围均在调控范围内。采用集中式方法调度时，该系统的综合调度最优解为λ=89.68 $/MW。

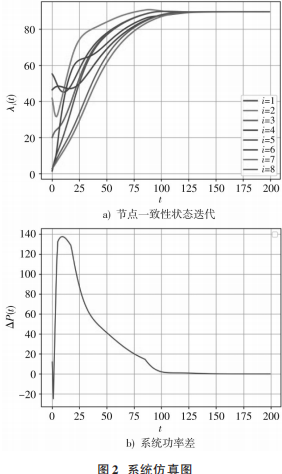
3.2 有效性验证

取kp=0.15，也即k1=k2=⋯=k9=0.15，收敛因子ε=0.03，仿真结果如图2所示。从图 2 中可以看出，与集中式调度结果相同，快速一致性算法的一致性变量在第151次迭代时也收敛到了λ=89.68 $/MW，表明该算法能实现系统的多目标调度，可以使系统达到最优运行状态，并且满足了系统的功率平衡要求。

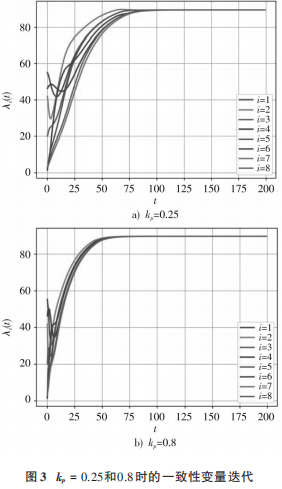
3.3 算法收敛速度的讨论

1）反馈增益kp对收敛速度的影响

收敛因子仍取ε=0.03，分别将反馈增益kp由 0.15增大至 0.25 和 0.8。由仿真结果图 3 可以看出：系统的一致性变量仍收敛到了λ=89.68 $/MW；kp=0.25时系统的一致性变量在第101次迭代时达到收敛，比kp=0.15 时的迭代次数提前了50次；kp=0.8时系统的一致性变量在第72次迭代时达到收敛，比kp=0.25 的迭代次数提前了29次。仿真结果表明，反馈增益kp在一定范围内取值越大，系统收敛速度越快，系统越能提前到达目标最优运行状态，越有利于系统的稳定运行。

然而当反馈增益 kp 逐渐增大到1.9时，系统不再收敛，如图4所示。说明适当的增大反馈增益有利于加快系统的收敛速度；若取值过大则会扰乱系统的稳定性，甚至造成系统的不稳定。

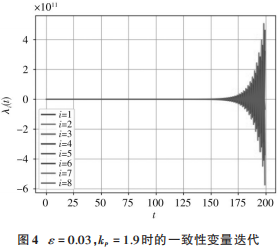
2）同时调节反馈增益 kp 和功率平衡调节系数 ε 对系统收敛速度的影响

由于 ε 为功率平衡调节系数，它的变化会影响“领导节点”的收敛速度，而“领导节点”收敛速度的改变会影响系统的收敛速度。因而，可进一步考虑同时调节 kp和 ε对系统收敛速度的影响。

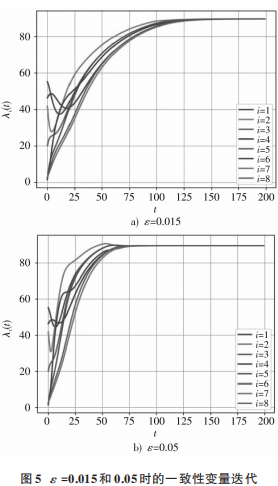
对比图3a），首先保持kp=0.25不变，ε分别取0.015和0.05，由仿真结果图5可以看出：当ε =0.015时，系统一致性变量在第160次迭代时达到了收敛（λ=89.68 $/MW）；当ε=0.05 时，系统的一致性变量在第86次迭代时达到了收敛（λ=89.68 $/MW）。由此可见，功率平衡调节系数ε在一定范围内取值越大，系统收敛速度越快。

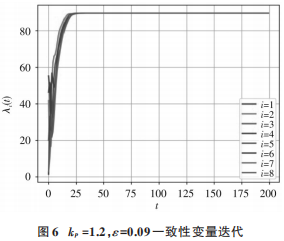
另取kp=1.2, ε=0.09，其仿真曲线如图6所示。由图6可以看出，系统的一致性变量在第27次迭代时达到了收敛（λ=89.68 $/MW），系统的收敛速度得到了显著提高。为此，在某些场景中，若对系统收敛速度有要求，那么在参数设置时可以考虑同时增大反馈增益kp和调节系数ε；另外，若kp和ε 同时取值过大，会造成系统的不稳定。

需要说明的是，通信网络的拓扑结构和“领导节点”的选择[15]等因素也会影响系统的收敛速度，在此不再展开讨论。

3）与传统一致性算法的比较

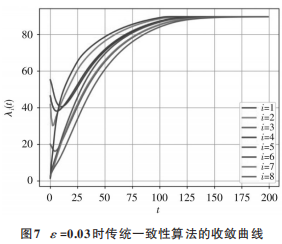
为了控制变量准确对比，将传统一致性算法中的 ε也设置为 0.03。从仿真结果图 7 中可以看出：系统采用传统一致性算法在第160次迭代时达到收敛（λ=89.68 $/MW）；而快速一致性算法通过调节反馈增益kp可实现在第72次迭代时达到收敛（见图 3b））。通过对比可知，快速一致性算法的收敛速度比传统一致性算法的收敛速度提高了2.2倍左右。因而，基于快速一致性的微电网调度不仅实现了系统功率的合理分配，还有效提高了收敛速度，时间复杂度更小，比传统一致性算法更加灵活应对微电网的各种状况。

3.4 应对负荷变动的验证

在实际调度过程中，高渗透的柔性负荷不可避免地会出现负荷波动，某些节点甚至会因为不可控因素突发故障，导致微电网的通信拓扑发生变化。采用该快速一致性算法，即使调度过程中负荷发生了改变，只要通信拓扑图是连通的，该算法仍然可以快速实现目标调度。以算例2中kp= 0.8 和 ε = 0.03 为例，在迭代次数t=100次时，因为一些偶然因素，柔性负荷机组 D3 退出网络调度，其他机组保持不变，仿真结果如图8所示。

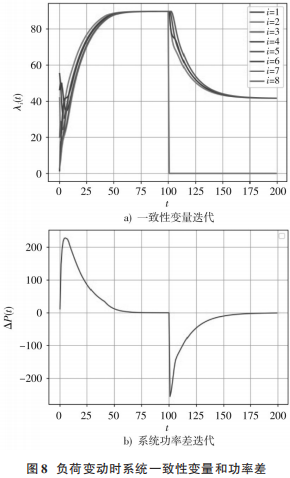
从图 8 可以看出，当柔性负荷 D3 退出时，余下机组的通信拓扑依然是连通的，就能保证各个机组的一致性变量达到收敛。系统也由原先的最优运行稳定状态（λ = 89.68 $/MW）进入到新的最优运行稳定状态（λ =41.60 $/MW）。因而，该快速一致性分布式结构更适用于处理拓扑变换和“即插即用”情况，具有更优的稳定性与可拓展性。

4、 结 语

针对包含传统燃料发电机、可再生能源发电机、柔性负荷与蓄电池的独立微电网多目标调度问题，本文提出了基于快速一致性算法的分布式优化调度策略，与传统一致性算法相比，能够以较快的运行速度实现微电网多目标调度。首先，建立微电网多目标调度模型，包括多目标优化函数和约束条件；其次，采用线性加权法和拉格朗日乘子法求该优化问题的最优解，设计快速一致性算法，并给出算法实施步骤；最后，在改进的微电网IEEE 14系统中进行仿真验证。仿真结果表明，该快速一致性算法在同等参数条件下比传统一致性算法的收敛速度更快，且满足了即插即用的要求，具有较高的可靠性。

在接下来的调度研究中，可综合考虑多个相互冲突的多目标多约束调度，目标函数除了环保和经济，还可以考虑用户满意度等，约束条件可以兼顾无功功率、电压及频率等，以完善和补充现有的电力调度策略。

审核编辑：郭婷