

纯电阻、纯电容、纯电感电路原理分析
电源/新能源
描述
上一篇文章我们解释了交流电路中,能量在电阻或电容上来回流动的概念,并正式介绍了「阻抗」的定义,以及用来计算阻抗的数学符号系统。
这一回我们要来看一些实际的电路,并试着运用这些数学工具来分析。
现实世界中没有纯电路
上一回我们介绍了纯电阻、纯电容、纯电感的阻抗在复数坐标系上的样子。纯电阻的阻抗只有实部,没有 j 项,因此画出来的阻抗就是在 X 轴上向右延伸。
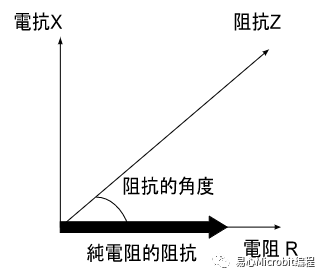
而在电感或是纯电容的电路中,阻抗只有虚数项 j 项,没有实部,因此画出来的阻抗就是在 Y 轴方向。向上为正的电抗,也就是电感性的电抗;向下为负的电抗,也就是电容性的电抗。
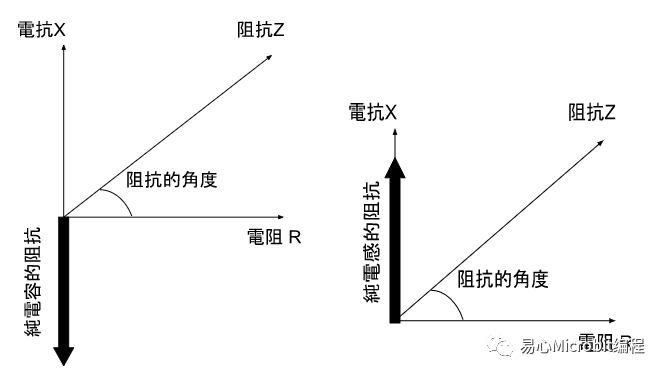
不纯砍头的蜂蜜也许有纯的,但现实世界中的电路没有纯的这种事。你拿起一个电感接到电路中,除非绕成电感的线圈是用超导材料做的,否则电感多多少少都会有些电阻,即使很小。
因此,现实世界中的电感应该是这个样子的:
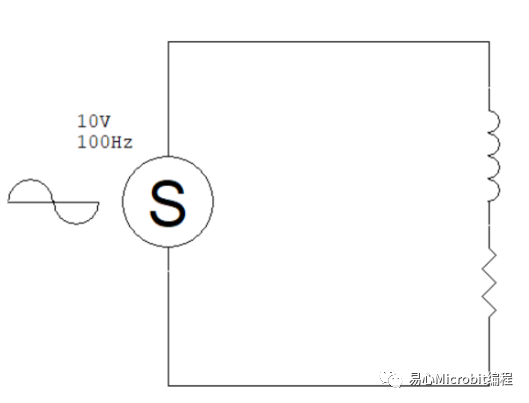
而它的阻抗就会是这样:
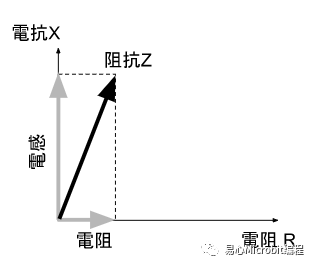
我们来看看有实际零件数值的电路要怎么计算。假设电路中的电感是 1 mH、电阻是 10 ohm,交流电源仍然是 10 Vpp、100 Hz。
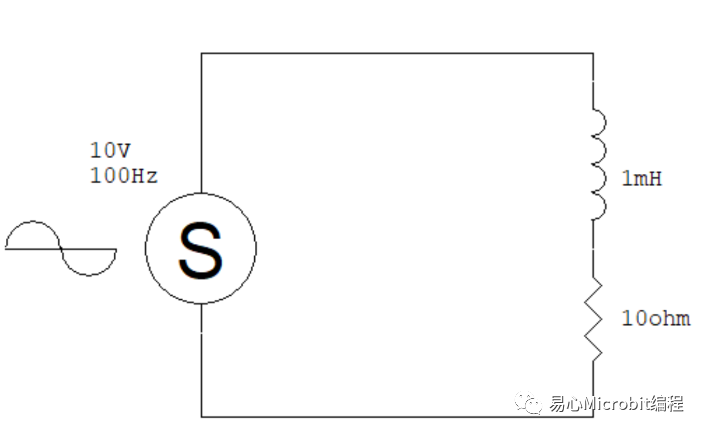
这里要特别强调一下,电阻的单位是奥姆(ohm)、电感的单位是亨利(Henry)、电容的单位是法拉(Farad),但在实际的电路中,我们常用到的电感数值范围可能是千分之一甚至百万分之一亨利,因此会用 mH(千分之一亨利)或是百万分之一亨利(uH)这样的单位表示。
电容数值也是类似的状况,我们很常用 pF(10 的负 12 次方法拉)或是 uF(10 的负 6 次方法拉),绝少直接用到 F 这么大的单位。
这个电路中,电感和电阻加起来的阻抗就是:
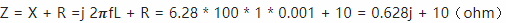
我们把这个结果画到复数坐标系上,看起来就是这个样子:
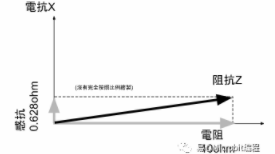
在真实世界中,由于几乎不可能有纯电感或纯电容的理想电路存在,大部分的情况下我们要分析的都是这样复数阻抗。
不纯的相位差
我们这几次在探讨的主题都是「电容或电感性负载会让交流电路中的电压和电流产生相位差」。在上面这个电路中,电压和电流之间的关系是什么呢?
我们先来看相位差。
根据之前讨论的,纯电阻性负载在交流电路中不会造成电压和电流的相位差,因此电压和电流之间的相位差就是 0。画在复数坐标系上,就是在实数的那条在线。
纯电感性负载会造成电压超前电流四分之一个弦波周期,用角度来算的话,一个周期是 360 度,四分之一周期就是 90 度,画在复数坐标系上,就是一条与实数轴呈 90 度夹角的线,也就是虚数轴。
聪明的读者可能已经想到,上图中「阻抗」那个箭头与实数轴的夹角,是否就是这个电路中电压超前电流的相位角呢?
没错,就是这样。这也是为什么我们要用这样的数学符号以及复数坐标系来分析交流电路的原因。我们可以用很简单的几何来求出电路运作的特性。
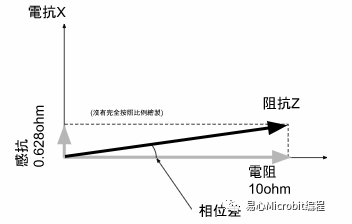
要求图中的标示「相位差」的那个角度
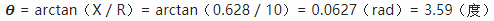
如果我们将这样的相位差画在图上,看起来就像是这样(先别管振幅的单位):
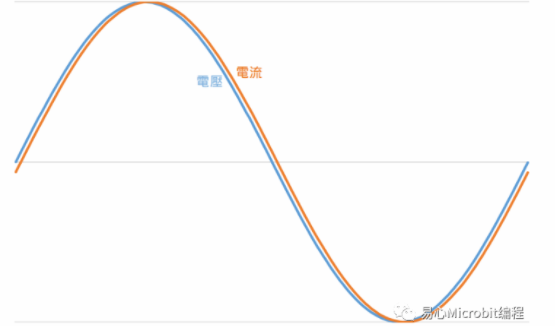
图中蓝色是电压波形、橘色是电流波形。在这个电路中,电压超前电流 3.59 度。3.59 度是一个相对来说蛮小的角度,因此可以看到电压和电流波形几乎重迭在一起,只有一个很小的相位差。
我们之前用过简化版的容抗、感抗公式来计算交流电路中电流的峰值。现在我们要来看看在实际的电路中要怎么计算。
在复数平面上画出来的那个「阻抗」的箭头,它与水平轴的夹角代表了电压与电流的相位差,而它的长度其实就代表了这整个阻抗的「大小」,英文用 magnitude 这个字,符号常用 Z。什么是大小呢?它就像电阻一样,在同样的电压之下,阻抗越大,电流就越小;阻抗越小,电流就越大。
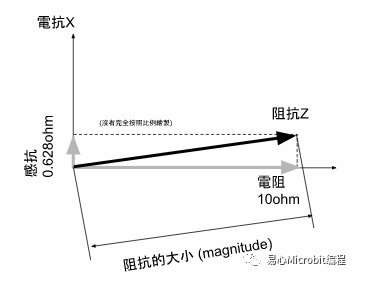
这个箭头的长度就是三角形的斜边,我们可以很容易用已知的两个边长(电阻大小与感抗大小)来求 SQRT(就是开根号的函数):
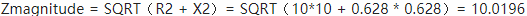
复数阻抗同样遵循奥姆定律 V = IR,因此拿峰值电压除以这个阻抗的大小,就可以得到电流的峰值大小。
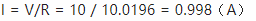
如果把电流和电压画在同一个图上,看起来就是这样:
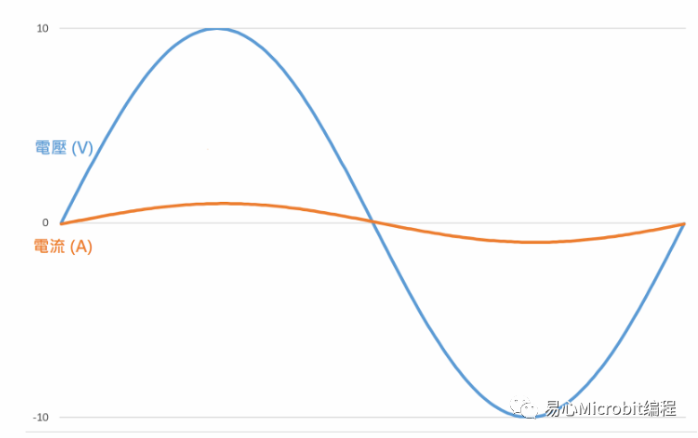
从刚刚的计算过程我们可以发现,由于电抗的部分只有 0.628j ohm,相对于电阻的 10 ohm 来说很小,这是因为不管是在计算相位差还是在计算阻抗的大小时,电抗部分的贡献都很有限,整个电路的特性仍然是由电阻在主导。
不过电抗的公式中有一项 f,表示电抗的大小会受到讯号频率的影响,但电阻不会,电阻就是电阻,它在 1 Hz 时是 1 ohm 的话,到了 1 KHz 时还是 1 ohm,这个现象会给交流电路带来很多复杂且有趣的特性…
小结
这一回我们利用实际的电路,示范了如何用阻抗的复数坐标系统来计算阻抗的角度所造成的电压电流相位差,以及阻抗的大小所决定的峰值电流。
下一回,我们要将「频率」这个因素考虑进去,继续探讨复数阻抗在交流电路中的许多有趣特性。
审核编辑:汤梓红
-
在纯电感电路中正确的关系是什么2024-07-23 3647
-
纯电感电路中电流和电压的关系是什么2024-02-27 10331
-
什么是纯电阻电路和非纯电阻电路2024-02-03 12628
-
纯电感电路中电流与电压的相位关系2023-11-15 21351
-
什么是纯电阻电路?什么是纯电阻交流电路?2023-07-05 6444
-
纯电阻交流电路分析2023-06-09 4980
-
纯电阻电路和非纯电阻电路的区别2021-08-20 15013
-
浅谈纯电阻电路与纯电感电路2021-06-30 3420
-
什么是纯电阻电路,纯电感电路又是什么2021-04-21 10787
-
纯电容电路定义_纯电容电路电流与电压的关系2018-02-27 66005
-
纯电感电路中电压与电流的关系解析2017-12-26 68038
-
一文读懂纯电阻电路和纯电感电路2017-11-02 17113
全部0条评论

快来发表一下你的评论吧 !

