经典卡尔曼滤波器的五个公式

‍先讨论滤波器的概念，滤波的意思是，让机器人在某个正确位置上对应的概率越高越好。

也就是可以理解为：把错误位置上的概率滤低，把正确位置处的概率滤高。

假设一个机器人小R在如下场景中出现，他刚开始不知道自己在哪（小R还没看到他眼前的门），因此他在这个场景中任何位置的概率是相等的。

如果此时纵坐标为机器人小R在对应位置处的概率，横坐标表示各个位置，应该是一条均匀分布的直线。

突然，机器人看到了眼前这个门，这里假设机器人提前知道一共有三个门，因此小R现在知道自己可能在任意一个门前，即三个门分别对应着一个正态分布。此时的概率波形可以理解为先验概率。

小R继续向前走到第二个门前，他通过自己身上安装的里程计发现自己走了d个单位。

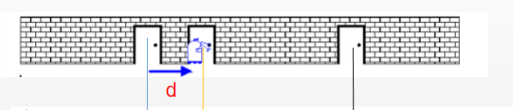
根据之前的概率分布，小R可以预测到，自己的位置应该向右平移了d个单位。那么可以将之前的概率分布向右平移d个单位，得到此时通过传感器得到的概率分布。此时的概率波形可以理解为似然概率。

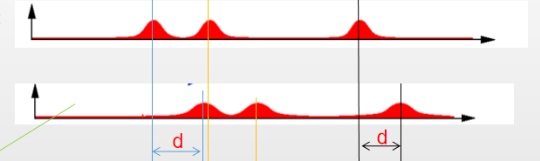
小R突然发现自己看到了第二扇门前，仅根据当前的观测，小R知道自己在三个门前的概率相同，又可以得到之前的三个正态分布。根据传感器预测得到的分布和根据先验信息得到的分布得：

两个波形信号可以做个卷积融合得到：

这样小R在第二扇门处（正确位置）的概率就变大了，在其他位置处的概率就变小了，进而达到了滤波的目的。

以上即是普通滤波器的直观解释，同样地，可以类比到卡尔曼滤波上。

由式(2)可知，新的不确定性由上一时刻不确定性预测得到，并加上外部环境的干扰。

这时我们对系统的变化有了模糊的估计，更新的状态（均值）和不确定性（协方差）分别如式(1)和(2)，预测的过程相当于之前的波形向右平移d个单位的过程。

得到的新的最优估计可以放到下一时刻不断迭代。以上就是经典卡尔曼滤波器的五个公式，给出了线性高斯系统的最优无偏估计。

我们可以用这些公式对任何线性系统建立精确的模型，对于非线性系统来说，我们使用扩展卡尔曼滤波，区别在于EKF多了一个把预测和测量部分进行线性化的过程。

此时再看这个高赞无公式推导的回答来回顾全局，一切豁然开朗

无公式直白解释卡尔曼滤波：

假设你有两个传感器，测的是同一个信号。可是它们每次的读数都不太一样，怎么办？
取平均。

再假设你知道其中贵的那个传感器应该准一些，便宜的那个应该差一些。那有比取平均更好的办法吗？
加权平均。（乘卡尔曼增益 K）

怎么加权？假设两个传感器的误差都符合正态分布，假设你知道这两个正态分布的方差，用这两个方差值，（此处省略若干数学公式），你可以得到一个“最优”的权重。

接下来，重点来了：假设你只有一个传感器，但是你还有一个数学模型（指的是上文中的预测模型）。模型可以帮你算出一个值，但也不是那么准。怎么办？

把模型算出来的值，和传感器测出的值，（就像两个传感器那样），取加权平均。

OK，最后一点说明：你的模型其实只是一个步长的，也就是说，知道x(k)，我可以求x(k+1)。

问题是x(k)是多少呢？答案：x(k)就是你上一步卡尔曼滤波得到的、所谓加权平均之后的那个、对x在k时刻的最佳估计值。于是迭代也有了。这就是卡尔曼滤波。（无公式）　　

      审核编辑：彭静