应用统计力学的框架探讨

统计力学和量子力学从历史上看一直是互帮互助共同发展的. 当把统计力学的框架应用到由纯粹的经典力学和经典电磁学描述的粒子系统时, 便会不可避免地产生佯谬以及与实验对不拢的结果. 其中, 对比热的研究可以说很大程度上暴露出经典力学的致命缺陷；对物质磁性的研究很大程度上暴露出经典电磁学的致命缺陷. 而这些致命缺陷的解决极大地推动了统计力学和量子力学的发展. 所以严格来看其实并没有经典统计力学一说, 所有被应用统计力学的系统必须完全基于纯粹量子力学的描述. 本文将以理想单原子分子气体, 理想双原子分子气体, 和理想非金属固体为例, 应用统计力学的框架探讨在经典力学描述和量子力学描述下这三种系统的比热, 并由此展示量子力学是如何克服经典力学对比热估计的缺陷的. 由于篇幅所限, 本文不可能从零开始讲起. 故假定读者已对热力学第0, 1, 2, 3定律, 能均分定理(注意它只是个经典定理), 正则系综框架下计算各种热力学量的基本流程(核心是计算配分函数)和量子力学的三个玩具模型(无限深势阱, 氢原子, 和谐振子)有初步的理解.

1理想单原子分子气体的比热问题

假定一个由 个完全相同的无相互作用的粒子构成的气体体系. 整个体系被关在一个体积是 的盒子里. 每个粒子只由一个原子组成(比如一些稀有气体). 由于粒子间没有相互作用势能, 故体系总能量就是每个粒子的平动动能之和. 考虑到每个粒子有 , , 三个自由度, 所以体系哈密顿量可以写成：

当我们考虑经典力学的表述时, 上式的 是连续变化的, 与之对应的广义坐标 也是连续变化的. 所以体系的正则配分函数是:

注意上式的 和 分别是量子全同性原理(全同粒子不可区分)和量子不确定性原理在经典配分函数中的体现(等效为这两个保留下来的因子). 但由于我们这果要计算的是内能 (然后由此得出比热), 即配分函数的对数对逆温 的偏导数, 而 因子中并不包含 , 所以对于本计算而言该因子只是个并不重要的常数. 将 的表达式代入配分函数然后化简得到：

所以体系的内能是:

很容易发现这个内能的结果和经典的能均分定理给出的结论是完全一致的. 在此基础上, 我们可以进一步求出比热:

所以在经典情形下算出的比热是一个与温度 无关的常数. 这个结果在高温下没问题, 但在低温下( 接近绝对零度时) 直接与热力学第三定律矛盾! 热力学第三定律要求熵和墒的一阶变化率(比热)在 趋向 K时必须为 0 ! 而上面这个比热的结果在趋向于 K时仍为 而不是0. 要解决这个问题就必须借助量子力学！

在上面的计算中, 我们采用的是经典力学对粒子的描述, 即 是连续变化的. 但如果采用的是量子力学的描述, 因为此时粒子被束俌在一个体积是 的点子里(也就是一个三维无限深势阱里), 那么根据量子力学里关于无限深势阱束缚态的结论, 就必然不是连续变化的, 而是只能取一系列分立的值:

其中 取正整数. 所以体系的哈密顿量可以写成:

由于此时状态是分立的, 所以体系的正则配分函数是：

代入 的表达式得到:

其中 . 在高温下, 很小, 所以上面的求和可以近似成积分:

因此可以看出高温下量子配分函数退化到经典情形的配分函数. 所以根据之前的计算结果, 高温下比热是 . 然而当温度 趋于0 K, 也就是 趋向 时, 前面说的求和近似成积分的技巧并不适用. 所以我们只能老老实实地回到量子配分函数的原始级数表示.

值得注意的是：括号内的级数并不是简单的等比级数, 所以我们并不能把它直接求出来. 但是注意到这个级数的每一项都比前一项小得多(因为此时 很大). 所以我们可以只取这个级数的前两项作为这个级数的近似, 以便于后面比热的计算. 所以在低温下量子配分函数可以近似成:

所以体系的内能是：

进一步求出低温下比热是:

可以发现当温度 趋于 0 K时,

所以在对粒子采用量子力学的描述以后, 低温下比热的行为恰好满足热力学第三定律!

2理想双原子分子气体的比热问题

考虑和情形（1）几乎完全相同的理想气体体系, 除了把里面的单原子分子都换成双原子分子 (比如氧气, 氢气,一氧化碳). 在使用质心坐标和相对坐标后,一个双原子分子的总自由度可以等效成 3 个质心平动自由度(这块和单原子分子没区别), 再加上比单原子分子多出来的内禀自由度, 即两个转动自由度 , , 和一个轴向的振动自由度(注意一个轴向的振动自由度其实对应到哈密顿量里两个独立的平方项, 即一个平动动能项和一个弹性势能项). 在经典力学的描述下, 根据能均分定理, 哈密顿量里每个独立的平方项都对应到 的平均能量. 一个双原子分子根据上述分析共有 7 个独立的平方项, 所以贡献 的平均能量. 所以 个双原子分子页献 的平均能量(也就是内能 . 所以比热 constant. 也就是比热是一个与温度 无关的常数. 而实验的观测结果发现比热随温度 的依赖关系是一个类似阶梯型的函数：在极高温下, , 随着温度降低, , 温度再降低, , 然后温度再降低到接近0 K, . 要解决这个问题同样也必须借助量子力学!

在量子力学的描述下, 一个双原子分子的平动自由度可以看成是三维无限深势阱模型, 转动自由度可以看成是氢原子模型, 振动自由度可以看成是一维谐振子模型. 所以根据量子力学中这三个玩具模型的结论, 我们可以写出 个双原子分子总的哈宓顿量:

所以体系的正则配分函数是：

所以体系的内能是:

其中

在情形(1)中已经处理过 . 所以我们现在着重看 和 . 当高温 很大也就是很小时, 可以被近似成如下的积分形式:

所以高温下转动能级部分给出的比热是:

此结果与经典的能均分定理给出的结论一致.

当温度 很低也就是 很大时, 完全仿照(1)中的逻辑, 因为原始的无穷级数难以计算, 所以我们只取该级数的前两项作为近似,

所以低温下转动能级部分给出的比热是:

可以发现当温度 趋于0 K时,

所以零温下比热是 0 , 满足热力学第三定律!

现在来看 . 容易发现 表达式里的无穷级数刚妤是个简单的等比级数, 所以:

在高温 下,   很小, 所以

所以高温下振动能级部分给出的比热是:

此结果与经典的能均分定理给出的结论一致.

当温度 很低也就是 很大时,

这个结果刚好对应零温时 个谐振子的总的基态零点能. 所以零温下振动能级给出的比热是:

满足热力学第三定律! 平动, 转动和振动能级都被冻结, 所以对比热的贡献是 0. 当温度从0 K逐渐升高, 最先被激发的是质心的平动自由度, 使得比热从 0 逐渐增加到 的平台. 继续往上升高温度, 内部的转动自由度也被激发出来, 使得比热从 的平台逐渐增加到 的平台 (室温就在比热差不多是 的区间里, 此时只有平动和转动自由度被激发). 再往上提升温度到极高温, 内部的振动自由度也最终被激发出来, 从而使得比热最终饱和至 的平台.

3理想非金属固体的比热问题(晶体比热问题)

考虑一个由 个原子构成的三维理想固体. 这 个原子在空间周期性排列组成晶格.  每个原子都在自己的平衡位置附近做简谐振动. 在简正坐标下, 这个系统可以被看成是 个独立的一维谐振子的联合. 在谐振子的经典力学描述下, 根据能均分定理, 每个一维谐振子哈密顿量里包含两个独立的平方项(一个平动动能项和一个弹性势能项), 所以贡献 的内能, 也就是贡献 的比热. 故 个谐振子的联合总共贡献 的比热.  这个 的比热是个与温度无关的常数. 所以很明显在低温下这个结果不趋于0, 所以与热力学第三定律矛盾! 然而, 如果使用谐振子的量子力学描述, 问题可以被顺利地解决! 在量子力学的描述下, 简正坐标表象下的哈密顿量可以被对角化成：

所以体系的正则配分函数是:

考虑最简单的情形：所有振子都是相同的频率 , 也就是谐振子的状态密度相对于频率(能量)的分布取成狄拉克delta函数的形式. (注：这种过于简化的态密度的取法被叫做 “爱因斯坦模型”, 更加合理的态密度取法是将其取成关于频率的二次式, 即所谓的“德拜模型”. 我们这里为了简化起见只考虑“爱因斯坦模型”). 此时体系的正则配分函数可以简化成:

所以体系内能是:

在高温 下也就是 很小时,

所以高温下的晶体比热是:

此结果与经典的能均分定理给出的结论一致.

在低温 下(趋于绝对零度) 也就是 很大时,

所以零温下的晶体比热是 0, 满足热力学第三定律!

图 1 和图 2 分别直观地给出了经典描述和量子描述下内能和比热与温度 的函数关系曲线:

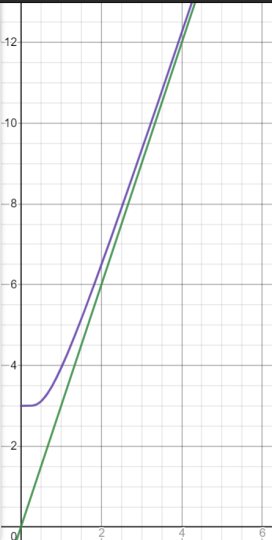图1 - 绿线是经典描述下的内能-温度关系, 紫线是量子描述下的内能-温度关系. 可以看出低温下由于量子效应显著导致紫线偏离绿线很大, 但随着温度升高, 量子效应越来越不明显, 导致绿线和紫线逐渐靠近直至基本重合. 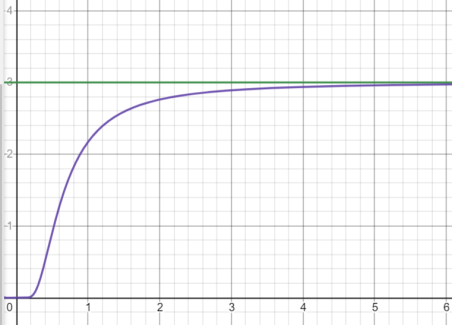图2 - 绿线是经典描述下的比热-温度关系, 紫线是量子描述下的比热-温度关系. 可以看出低温下两者有巨大的差别. 经典的能均分定理给出了非零的常数比热. 而使用了谐振子的量子描述以后, 绿线被修正成了紫线. 此时低温下满足热力学第三定律同时高温下退化成经典的绿线！

　　

      审核编辑：彭静