一种类似于ICP算法的三维点自动配准方法

<问题描述>

传统经典的方法就是ICP算法，Besl于1992年提出，称为ICP（最近点迭代算法）。该方法将输入的两片点云分别记为源点云P和目标点云Q，通过遍历搜索找到P、Q之间所有点的对应关系得出变换矩阵H，最后以两点距离的平方和作为目标误差函数，不断迭代计算，直至满足一定的误差收敛条件。

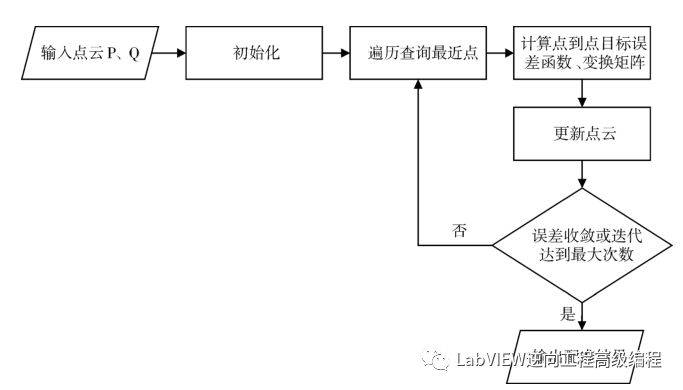
这个问题在很多方面都会遇到，比如相机的外参标定，在世界坐标系放置几个点，相机a在自己的坐标系下面看到的坐标是a1,a2,a3...an，相机b在自己坐标系下面看到的是b1,b2,b3...bn，如何将将相机a两个相机统一到a的坐标系下面。此时就会用到点的配准。

使用三维扫描进行物体扫描，要将一个物体完整的建模需要多个视角连续采集，每个视角相机的姿态都会存在变化，视角之间需要配准，通常的方法是在物体表面贴Marker点，通过识别Marker点的坐标，快速配准然后再局部优化。

Nonlinear Curve Fit 最适合输入数据点集（X，Y）的参数集，如非线性函数Y＝f（X，a）所示，其中a是参数集。该方法使用Levenberg-Marquardt（列文伯格-马夸尔特）算法，是使用最广泛的非线性最小二乘算法。

使用这个函数来优化迭代找到最优的变换矩阵，核心是设置这个迭代的VI。
 

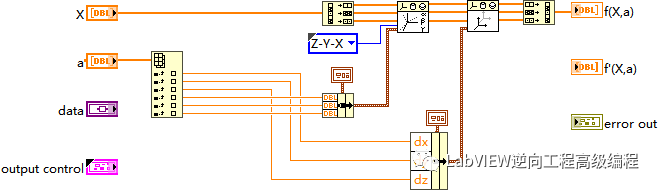
输入点先进行旋转计算，再进行平移计算，最后输出变换后的点集，通过迭代使得输出变换后的点集Q与目标点集P的差值最小。
 

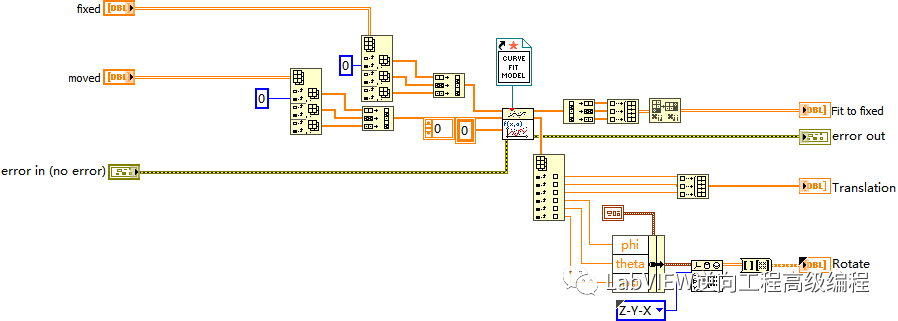
将源点云和目标点云变换为1D数组，通过Nonlinear Curve Fit 迭代，最后输出变换后的RT（旋转矩阵和平移向量）。

<结果验证>

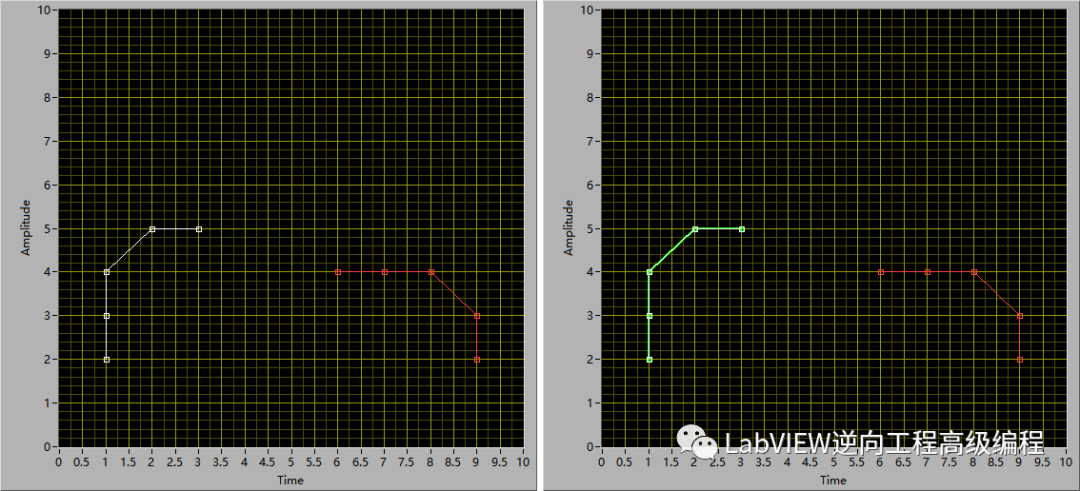
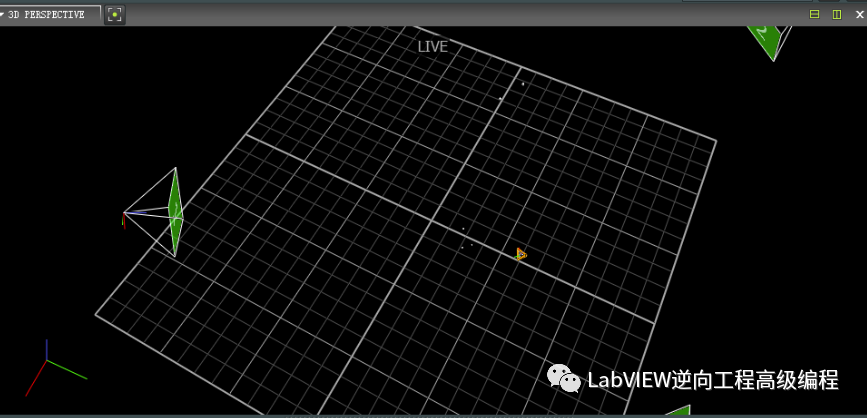
白色点是源点云P，红色线是目标点云Q，绿色线是配准后的Q，结果配准后的Q与源点集P重合。

这里提供了一种类似于ICP算法的一种方法，希望对大家有所启发！

审核编辑：刘清