

传递函数的三种形式及应用场合
描述
传递函数表示线性定常系统自身,将输入信号变换成输出信号的能力。这是线性定常系统自身的特点,一个不同的输入就会有一个不同的输出。输入信号本身不影响传递函数,传递函数是我这个系统自身决定的。
获得传递函数的方法多种多样,可以直接使用微分方程进行变换,也可以使用复阻抗法求取。但重要的是变换传递函数的能力,针对不同应用场合,变换传递函数的形式。阅读传递函数的能力,比如通过传递函数能否看出系统极点和零点的位置,以及增益。
根据线性网络理论,由电容、电阻和电感组成的电路网络,其传递函数H可以用如下通用式表示:
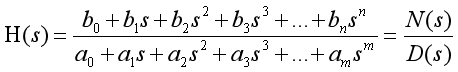
在这个式子中,很重要的一点是分母的阶数m必须大于或等于分子的阶数n。当m>n时,H(s)的幅值会随着s趋于无穷而趋于0,满足该性质的传递函数为”严格正则”。分母多项式D(s)阶数反映了该电路网络的阶数。让分母多项式D(s)=0,解出的所有根称为系统的极点,让分子多项式N(s)等于0,解出的所有根为系统的零点。
传递函数是一个分式,分子和分母都是多项式。基于应用场合的不同,它有三种常见的变换形式:
第1种传递函数写法:在因式分解的时候,使s的最高项系数为1时。这种形式一眼就可以看出它的零点和极点。这个形式是传递函数根轨迹形式,也称为首1型传递函数形式。这个时候提出来的常数,叫作根轨迹增益。应用在根轨迹的场合。
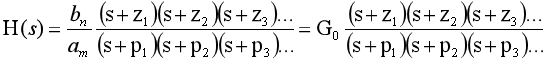
第2种传递函数写法:在作因式分解的时候,常数项全部提出来,常数项变为1,通俗的说我们叫尾1型传递函数形式。这个时候提出来的系数我们叫作环路增益或者叫开环增益。应用在bode图绘制,奈氏图绘制,系统开环频率响应分析的场合。
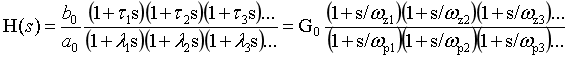
这两个系数有什么关系,b0和bm有什么关系,b0=bm*z1*....zm。从数学角度看,就是提取公因式的事情,提的大和提的小的问题。提的小是前面的系数,提的大是后面的系数。
第3种传递函数写法:当传递函数带有积分环节,可以写成这种形式。这种形式应用在环路补偿的场合。
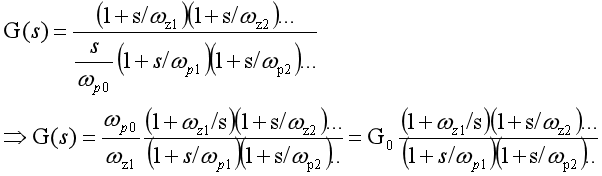
wp0是什么呢?
引入一个概念,称为“0dB穿越极点”。对于包含原点极点的传递函数,也就是当s=0时,传递函数的幅值趋于无穷大。通常原点极点的s会带有一个系数,例如1/[sRC(1+...)],可以将其重写为如下形式:
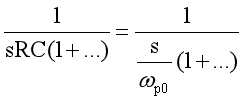
式中,wp0就是“0dB穿越极点”,它在上式中等于1/RC,对应截止频率,也就是说s=wp0时,wp0/s的幅值等于1(或0dB)。
下图种画出了wp0/s的幅值与频率的关系,是一条斜率为负的斜线。
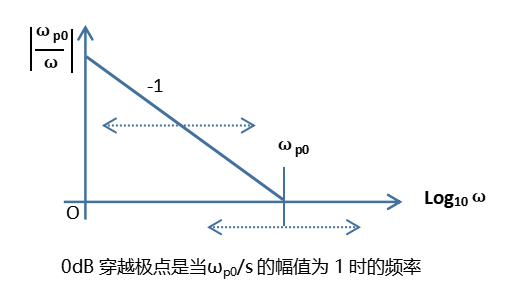
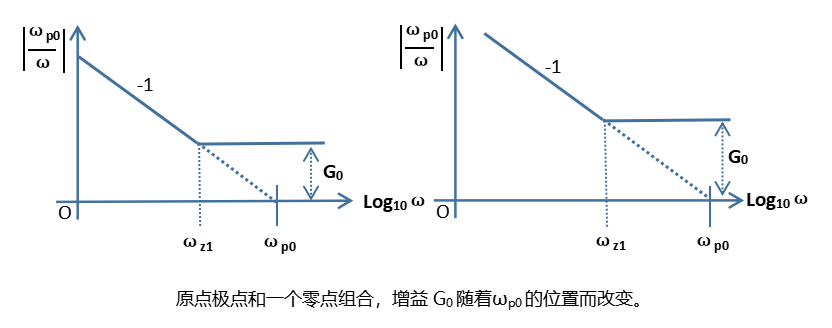
当原点极点与一个零点组合在一起时,斜线会在零点频率处转折并维持在增益G0,G0称为中频增益。下图显示了不同wp0的幅值-频率关系。
审核编辑:汤梓红
- 相关推荐
- 热点推荐
- 传递函数
-
传递函数的定义是什么 传递函数的拉氏反变换是什么响应2024-02-01 8389
-
传递函数和控制Block(上)2023-11-17 2416
-
如何建立传递函数?2023-09-28 2518
-
开环传递函数是怎样影响系统的?2023-07-11 5684
-
如何列写无源网络传递函数2023-03-10 6693
-
放大器的传递函数-误差放大器、电压放大器、电流放大器的传递函数导出2023-02-24 4727
-
传递函数极点和零点的影响是什么2021-06-12 11254
-
斜率的传递函数:电压模式的传递函数2018-11-30 2828
-
传递函数的频域辨识2017-10-26 1985
-
自动控制原理_传递函数2016-01-18 1017
-
传递函数中零点的解决方案2010-12-24 5074
-
基于Butterworth标准传递函数设计2009-06-11 921
全部0条评论

快来发表一下你的评论吧 !

