

工程问题的有限元分析到底难在哪里呢?
电子说
描述
2003年春,记得田宗漱老教授在中国科学院研究生院的有限元课上曾提及一件事,国内某项重点工程的甲方单位委托国内多家科研机构背靠背地分头对该项目进行了整体结构分析,后来结果汇总到一起,专家组经过反复的研究论证,判定国内一家985高校的计算团队给出的结果是错的,因其采用的一些计算假定不符合实际情况。
一所名校的专业仿真团队,耗费数月时间,投入大量人力,对这个项目的分析竟以失败的结果而告终。这个真实发生的事情说明,实际工程问题往往都是难度比较大的问题。专业团队小心翼翼地计算,花费数月时间尚且出错,那么可想而知,对于大量研发力量薄弱的中小企业,缺乏专业经验,有些甚至没有专职分析人员的情况下,要真正地具备仿真分析能力会有多困难。
那么工程问题的有限元分析,到底难在哪里呢?这是一个很大的题目,本文仅结合几个具体的算例和个人认识作简单讨论,希望能抛砖引玉,引起广大分析人员的思考。
首先来看第一个算例。如图1所示,一个100mm×100mm×1000mm的长方块体,材质为结构钢,弹性模量200GPa,泊松比0.3,屈服强度200MPa,理想塑性(不考虑硬化),材料应力应变关系如图2所示。整个构件轴向受压。

图1 轴压柱形构件
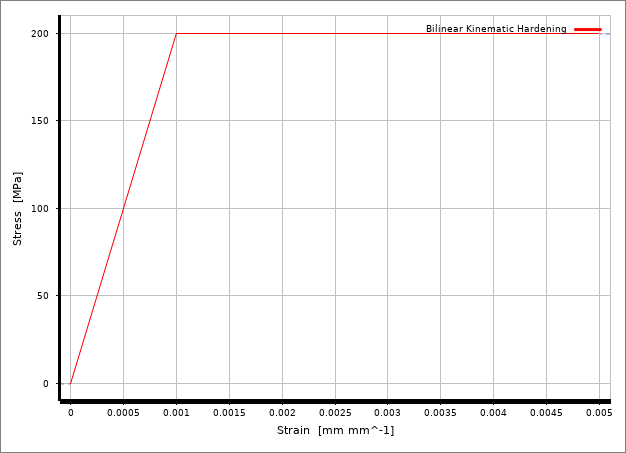
图2 理想塑性材料模型
读者可能会说,一个构件单轴受压,这能有什么问题?计算中采用了图中所示的一端固定(ANSYS Mechanical中的Fixed Support),另一端位移加载的方式进行模拟,顶部向下加载位移量0.8mm。
计算结果表明,构件的中上部接近单轴应力状态,从轴向变形来看,名义轴向应变绝对值仅为0.0008,并未达到单轴屈服应变0.001(fy/E),Von-Mises等效应力几乎等于轴向应力,即0.0008×200GPa≈160MPa。但是由于泊松效应,底面附近位置实际上是处于复杂的三轴应力状态,而且这一看似再平常不过的固定约束还引起了应力奇异。
如图3所示,计算出的最大Von-Mises等效应力SEQV的数值为215.52MPa,竟然违背了在Engineering Data中定义的理想塑性关系,明显超过屈服强度。这时可能有人要问,花了百十来万买来的软件,难道连本构关系都不满足?由此可见,即便对于这样一个单一构件的简单受力问题,边界条件的选取都是一件值得推敲的事情。
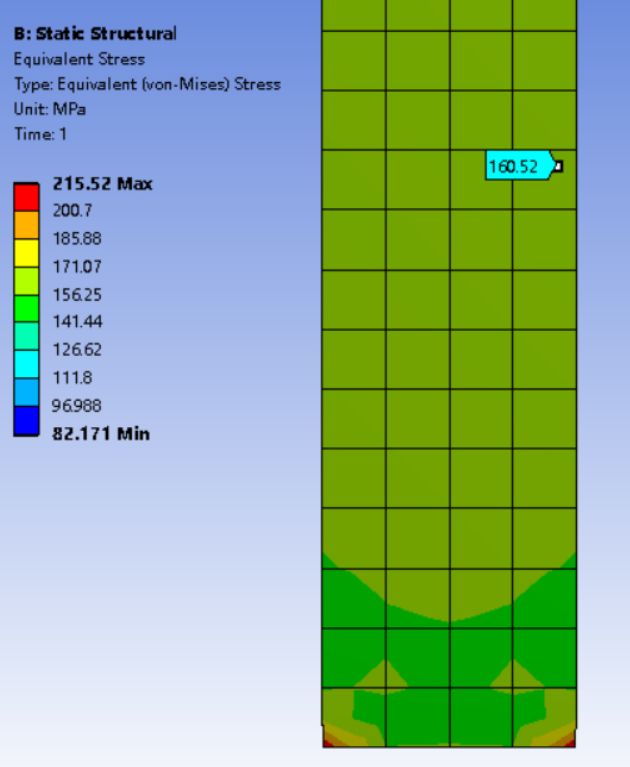
图3 计算的Von-Mises等效应力分布
其实,在很多其他场合也可能出现类似问题,如图4所示,两个圆环A和B截面尺寸分别为3mm×5mm以及3mm×3mm,其接触面存在4.5微米的几何干涉,定义摩擦系数为0.1的Frictional接触,B外侧为固定,通过2D轴对称分析计算两钢环之间的过盈配合问题。
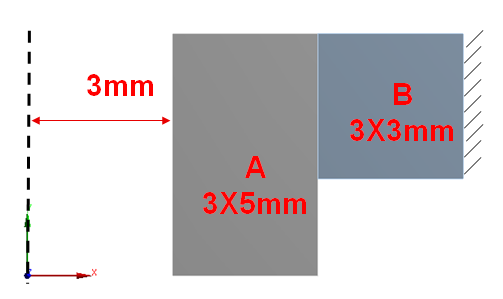
图4 轴对称问题示意图
图5为分析中采用的双线性硬化模型,切线模量很低,即便塑性应变达到屈服应变的5倍,后继屈服强度也会不超过205MPa,但是计算的von-Mises等效应力结果却也是出现了明显超过屈服强度的数值,最大值为218.78MPa,如图6所示。
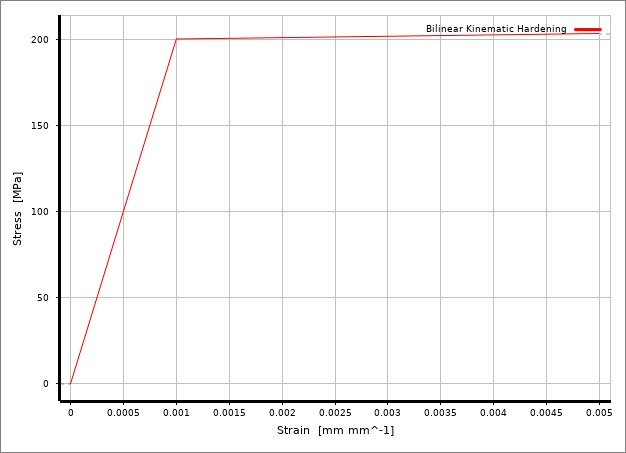
图5 硬化材料模型
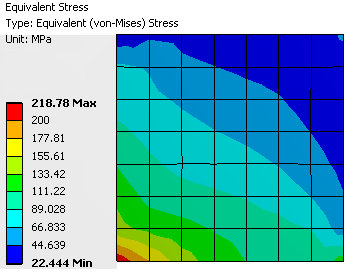
图6 等效应力分布结果
这类现象估计也经常出现在很多用户的计算书中,而且不论你进行的是线弹性分析,又或者是理想塑性条件下的弹塑性分析,都是同样的结果。其实在有限元分析中还有很多这类问题,认真推敲起来,还真的就是越想越不对劲儿,有种“看山不是山”的错觉。
再来看一个结构动力学分析的简单例子。这是以前西安地区的用户发来的一个问题,问题来源是高等教育出版社出版的同济大学朱慈勉教授主编《结构力学》下册中的一个结构动力学例题,如图7所示。

图7 结构动力学例题
这是一个很典型的动力学题目,需要验证跨中电机运转时梁的强度和变形。在有限元分析中,当然首先需要计算位移,也就是梁的挠度。这个用户是能够熟练操作ANSYS软件的,他根据电机运转频率,在结构上施加了一个随时间正弦变化的函数荷载,对结构进行了瞬态分析,计算时间为10个运转周期,施加的荷载时间历程及计算的梁跨中挠度时间历程曲线分别如图8和图9所示。
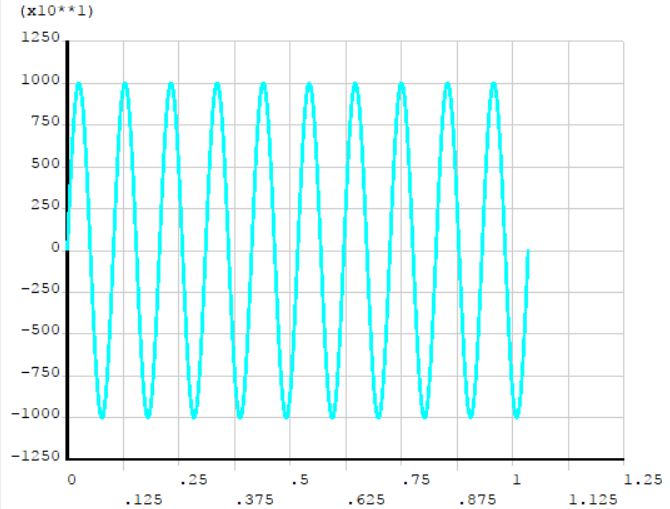
图8 用户施加的正弦荷载曲线
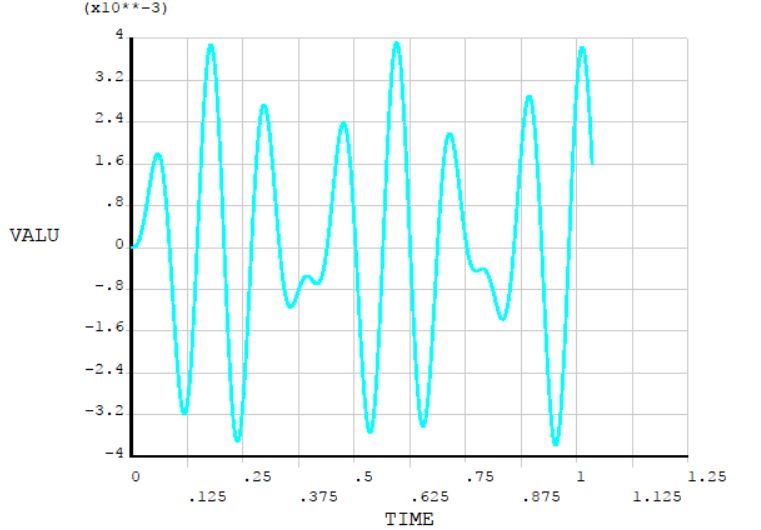
图9 用户得到的跨中挠度瞬态过程曲线
根据计算结果,用户说梁跨中的最大挠度仅约为3.78mm,与教材中计算挠度结果6.5mm差别很大,表示无法理解。实际上,之所以出现这样的问题,是因为分析人员缺乏结构动力学以及ANSYS计算原理方面的理论基础。
我建议他采用谐响应分析来计算这个问题,计算后得到的挠度结果约为1.7mm,表面数字来看与教材计算的结果反而差距更大了。之前在一些讲座中,明显看到很多听课学员疑惑的眼神。标准的谐响应计算,只有一个荷载,不会有问题,书上的结果当然也是对的,那么问题又出在哪里?
以上这些还都是一些结构形式简单、受力状态明确的结构计算问题,那么对于一般的更为复杂的实际工程问题,可想而知,计算过程中必然会有更多的难点需要去克服。
我在编写的《ANSYS结构有限元高级分析方法与范例应用(第三版)》(中国水利水电出版社,2015)一书中首次提出有限元分析的“二次映射”思想,即:分析人员首先需要将工程问题映射为可以求解的力学(物理)问题,再将这些问题映射为ANSYS等计算软件所能求解的数学问题。
在第一次映射中,需要分析人员具备相关的力学背景知识,能够把待求解的实际工程问题抽象为一个完整描述的力学问题,包括能确定求解域以及全部的边界条件、初始条件,最好能够画一个计算草图出来。这个过程中,需要随时思考一系列问题:
计算域取到这个范围是否合适?这个范围的边界是否都可以明确下来?这个问题需要求解的力学方程是什么(也就是问题的物理机制或特点,比如:空间轴对称问题和三维问题的平衡方程当然不同,板的分析方程与连续体的方程当然不同,弹性和弹塑性的求解方程当然不同,静力学和动力学的求解方程当然不同,等等)?这一次的映射相当于给要分析的问题定性。
第二次映射,则需要分析人员熟悉计算软件的功能和应用,能够把一个明确的物理问题转化为软件语言,即软件可以数值求解的数学问题。第一次映射中确定的计算域,如何在计算软件中创建出来(用什么样的单元类型或类型组合来描述求解域)?外部激励和边界条件如何施加能反映实际受力状态?需要调用软件的何种求解模块进行计算?比如,上面的梁的振动问题,就需要映射到谐响应分析模块而不是瞬态分析模块。这一次映射相当于进行建模计算工作过程的一个规划。
两次映射之后,结构分析的任务也就明确下来,就可以着手于具体的建模和计算操作了。由此可见,对工程问题的抽象和定性的能力、对力学理论及软件编制原理的认知、对软件功能和应用的熟悉程度都会在不同程度上影响问题是否能够得到圆满的解答。
这其中还会涉及到模型的简化、对称性的应用、计算参数的选择、非线性收敛问题的克服、对分析结果的解释等一系列具体问题,这些问题环环相扣,可以说每个环节都不容易。尤其是对于复杂问题计算结果的解释,论证这么一个基于虚拟网格的数值现象跟实际复杂物理现象之间的一致性程度,如果发现不合适的就要回去修正模型重新计算。
对于一些问题中的复杂之处,往往是需要分析人员首先充分理解数值现象的产生机理(计算原理),然后再来解释这个数值现象在多大程度上反映了真实物理现象。
一致程度高就是通常所说的仿真,否则就是失真(或者干脆叫做“仿假”)。而且这个领域还有一个特点,就是一些与概念有关的经验问题,往往是可意会而不可言传,向前辈请教,他们好像也说不出个什么,但是这些经验又是一种真实的存在,这时你千万别误以为前辈不想帮你。
综上所述,有限元分析的确不是件容易的事情,它更不是一个随便什么人都可以玩的数值游戏,它客观上需要分析者熟悉相关领域的产品结构和设计过程,具有力学和数值分析的理论根基,还得能熟练操作相关的分析软件,对人提出了比较高的要求。
对于一些根基不牢,甚至连材料力学都没有学过的分析者而言,做有限元分析简直无异于“裸奔”!之前看到一些连应力和力的区别都讲不清楚的用户也在分析一些具体问题的时候,说实在话,真的替他捏把汗。
在本文的最后,打个比喻,不妨把分析人员的状态归纳为三个境界。
一开始学习计算软件,不论是分析简单的悬臂梁还是开孔的方板,感觉入门很快,像麻将桌上的很多新手,手气往往不错,而且有些单位有固定的分析模板,又有前辈指导,进步就比较快,正所谓“看山是山,看水是水”,这是分析者的第一境界。
当新手随后实践到了一定程度,开始分析一些复杂的项目或者由自己主导来分析一些具体项目时,各种问题和疑惑也会接踵而至,而且在无数次加班甚至可能经历数个晚上住在办公室,但最后还是被软件完虐,感觉问题越来越多,有的问题甚至想半天也想不明白,前景也越来越看不清。一方面是艰辛的付出,另一方面却看不到成果,由此而开始失落、甚至怀疑做这个的意义,这时的感觉恰似“看山不是山,看水不是水”,这是分析者的第二境界。
然而,越是在困难的时候,越是要坚持“去粗取精、去伪存真、由此及彼、由表及里”的研究态度,具体问题具体分析,沉下心来,不断去积累知识与经验,相信在一番彻悟后定能到达“看山还是山,看水还是水”的佳境。
审核编辑:刘清
- 相关推荐
- 热点推荐
- ANSYS
-
六相感应电机转子感应电压有限元分析与研究2025-06-10 183
-
有限元分析2008-06-17 5986
-
MATLAB有限元分析与应用2011-02-28 13326
-
如何有效的学习CAE有限元分析2020-07-07 1569
-
求一种有限元分析中PCBA的简化建模方法2021-04-19 1760
-
光纤电场传感器的有限元分析2009-07-17 603
-
有限元分析及应用_曾攀2011-05-02 2106
-
有限元分析讲座2011-05-06 649
-
abaqus动力学有限元分析指南2016-05-11 1444
-
采用环梁加固风机基础的有限元分析2017-01-02 870
-
基于Ansoft的开关磁阻电机有限元分析与研究2017-01-21 1115
-
Ansoft工程电磁场有限元分析2017-04-01 1728
-
有限元分析相关知识的解析2017-11-12 1380
-
基于箱形梁CADCAE有限元分析2021-07-26 828
-
动力学有限元分析教程下载2021-12-06 872
全部0条评论

快来发表一下你的评论吧 !

