

毫米波雷达与摄像头单应性变换标定方法误差因素分析
描述
摘 要 :目前在交通监测领域中毫米波雷达和摄像头已经被大量使用,传感器融合可以弥补单一传感器的劣势,做到优势互补,两者融合需要标定出传感器间的空间转换关系。对于毫米波雷达与摄像头空间转换关系已有文章提出一种基于单应性变换原理的交通监测毫米波雷达与摄像头标定方法,该方法只需提取交通监测场景中目标在两传感器中对应的坐标点对就能解算出传感器间的转换关系。相比传统方法对摄像头内参数、传感器自身以及传感器之间的旋转角度等参数进行标定,该方法更加简洁有效,可以更高效的解决坐标转换问题,但目前还缺乏对影响单应性标定方法误差因素的分析。针对这一问题,文中将通过实验对单应性标定方法中特征点空间分布以及数量对于标定精确度的影响进行研究并给出合适的标定方案。
0 引 言
根据世界卫生组织(World Health Organization, WHO)报告数据 [1],每年有大约 135 万人死于道路交通事故,平均每 24 s 就有 1 人在道路上失去生命 ;道路交通伤害是 5 ~29 岁儿童和年轻人的主要死因,全球道路交通安全形势严峻 [2-3]。交通事故的频发给人们的生活健康和经济产生了巨大影响,所以优良的交通监测技术对人们的生活有着重大意义。目前在交通监测领域,较为普遍的是使用单一光学摄像头对车辆进行识别跟踪或者使用雷达对车辆进行测速测距。但是这些传统的监控方式都存在一定的局限性,光学摄像头可以获得较为丰富的目标及场景的纹理特征,但其测速测距能力较弱,且光学传感器容易受到天气、光照等因素的影响。而毫米波雷达在测速测距以及抗天气干扰等方面具有天然的优势,但却无法获得目标的纹理信息等特征。将光学摄像头与毫米波雷达传感器进行融合可以做到优势互补。因此,光学摄像头与毫米波雷达信息的融合已成为智能交通系统的研究热点 [4]。
在进行传感器数据融合之前,首先要通过传感器标定来解决毫米波雷达与光学摄像头间的空间转换问题。目前已经有学者研究出了一些较为有效的毫米波雷达与光学摄像头标定方法。日本丰巴技术中心研究人员研发出了基于毫米波雷达和摄像头的障碍物检测分类系统,首先利用摄像头获取图像,使用毫米波雷达选出并建立感兴趣区域,然后利用神经网络进行待测车辆识别,但这种方法识别效果的精确性较差[5]。Nabati,Ramin & Qi[6] 等提出了一种中心融合的深度学习网络,实现了雷达与摄像头的融合,该方法为车辆检测建立了立体的视锥而不再是检测框,从而提高了自动驾驶过程中2 个传感器标定及融合的准确性。张富有 [7] 提出一种通过标定摄像头内参数以及毫米波雷达与光学摄像头三轴旋转自由度的方法来解算空间转换关系,从而实现传感器间的标定。但这种方式需要标定的参数过多,增加了实验难度,并且摄像头标定误差也会受多种因素影响 [8-9]。已有文章提出一种基于单应性变换的毫米波雷达与摄像头标定方法,该方法通过在毫米波雷达与摄像头共同采集区域中设置定标物,然后提取定标物在雷达数据以及摄像头像素数据中的坐标形成特征点对,通过多个特征点对可以标定出两者的空间转换关系。但基于单应性变换的毫米波雷达与摄像头标定方法缺少对影响标定误差的因素的分析。
基于单应性变换的毫米波雷达与摄像头标定方法缺少对影响误差因素的分析,本文将通过实验从特征点空间分布以及数量对单应性标定误差的影响进行分析。
1 单应性标定原理及误差建模
1.1 毫米波雷达与摄像头单应性标定原理介绍
单应性变换原理常被应用于图像领域,比如相机成像可以把现实世界中的三维目标表示在二维的像素平面中。由此单应性变换可以用来表示三维目标点与二维目标点之间的映射关系 [10]。毫米波雷达采集的目标数据为二维坐标 (xr, yr),而摄像机采集的目标像素点坐标为 (u, v),假设雷达检测到的目标以及摄像机检测到的目标全部在雷达采集平面 xroryr与像素平面 ucocvc 上,如图 1 所示。
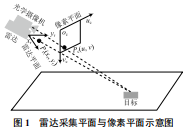
图 1 所示为一个在毫米波雷达与摄像头公共视场内的目标,假设其在毫米波雷达坐标下的位置为 Pr(xr, yr),在摄像机像素坐标系中的位置为 Pc(u, v)。由单应性变换原理可知,标定雷达采集的目标点与摄像机像素坐标之间的空间转换关系就是标定雷达采集平面 xroryr 与像素平面 ucocvc 之间的映射关系,根据单应性原理可得雷达采集平面与图像像素平面关系 :

式中,H 为雷达平面与像素平面之间的单应性矩阵,其表示两个采集面之间的转换关系,H 是一个 3×3 的矩阵,s 为常数。雷达采集平面和像素平面之间的关系可以通过估计单应性矩阵 H 得到,此过程不需要对摄像机内外参数等进行单独标定,也不需要对各坐标轴旋转角度进行标定。根据式(1)将单应性矩阵展开可得:
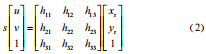
将式(2)展开可以得到 :
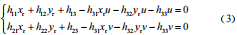
在雷达平面与像素平面取 N 个对应的目标点对,带入式(3)化为矩阵则有 :
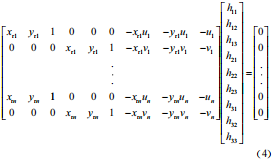
式(4)左矩阵为 2N×9 阶的矩阵,右部分矩阵为 9×1 阶的矩阵,记为单应性矩阵 H。最小需要 4 个不共线的特征点对可以求解出单应性矩阵,并且对于超定方程组,可以通过最小二乘法求解,但为了减少数据中噪声对单应性矩阵标定的影响,采用最小中值估计的方法来增加 H 的准确性和鲁棒性。定义每个标定出的单应性矩阵 H 的标定误差为:
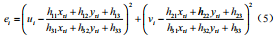
最小中值优化估计实现步骤如下 :
(1)对于包含 N 对特征点的集合,每次随机抽取 4 个特征点对组成一个集合 ;
(2)对于每一个样本集,使用最小二乘法估计得到一个单应性矩阵 hi ;
(3)对于每一个 hi,可以求出整个数据集所有点对的标定误差 ei,再找出 ei 的中值 emedi ;
(4)求解出使 emedi 最小的 hi。通过上述方法可以求解出毫米波雷达与摄像头之间的单应性矩阵,只需采集一定数量的定标物特征点对就可以完成毫米波雷达与摄像头之间的标定,实现毫米波雷达坐标与像素坐标之间的转换。
1.2 误差因素建模
根据式(2)可知,单应性标定法中如果获得一定数量的特征点对,即成对的 (xr, yr) 与 (uc, vc) 就可以求解出单应性矩阵,并且由于单应性矩阵实际是一种超定方程组,因此求解至少需要 4 对特征点对。但是特征点对的数量选择多少以及特征点对选取的位置对标定精度产生的影响需要进一步实验探究。针对单应性变换标定方法将其标定误差与其影响因素定义如式(6)所示 :

式中:etotal 表示标定的总误差;r 为雷达自身采集误差;l 为特征点空间分布的位置;n 为特征点数量。公式说明标定总误差为3 个误差因素共同作用下产生的结果。在这 3 个误差因素中,雷达采集误差受雷达硬件自身测距精度与测角精度的影响,因设备差异的不同会导致不同测距测角精度误差。
2 实验分析
2.1实验设备介绍
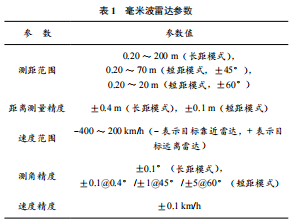
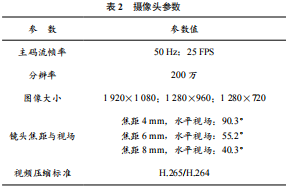
本文采用的实验设备为77G 大陆 ARS408 毫米波雷达以及海康威视光学监控摄像头,设备如图2 所示,雷达采集界面示意图如图3 所示,雷达采集数据示意图如图4所示。毫米波雷达参数见表1 所列,摄像头参数见表2 所列。

2.2 误差实验分析
在本节将对提出的标定模型中各因素进行实验分析,研究特征点对空间位置分布以及特征点对数量对标定精度的影响。设计实验在操场上利用摄像头与毫米波雷达对不同位置的角反射器进行采集。雷达采集数据包含纵向距离 xr,横向距离 yr,纵向速度 vx,横向速度 vy 以及 RCS 等信息。摄像头采集的数据中,角反射器的位置为像素坐标 (uf, vf)。本次实验将在毫米波雷达与摄像头的公共采集视场中放置角反射器,每一个角反射器都可以从雷达数据中提取出其坐标位置(xr, yr) 以及其在摄像头数据中的像素坐标 (uf, vf),由此形成一组特征点对,通过不断改变角反射器的位置从而获得不同的特征点对。
2.2.1 雷达设备采集误差
由于毫米波雷达设备硬件本身在测速和测角方面存在一定的误差,这也会给单应性变换标定带来一定的误差。根据表 1 所列的毫米波雷达参数,可以制作图 5 所示的毫米波雷达设备采集误差模型。
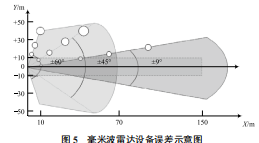
图 5 中,红色区域代表雷达远距离扫描模式,蓝色区域代表近距离扫描模式,白色圆圈代表此处目标的位置测量误差,圆圈的半径越大代表误差越大。根据此图可知,目标距离雷达越远相对角度越大,位置测量精度会增大,故绿色区域为较为合适的采集区域。实验根据雷达误差模型选择雷达纵向 50 m 以内,横向 ±10 m 内的范围作为实验区域,以降低雷达设备误差对标定精度的影响。
2.2.2 特征点空间位置构型实验
标定误差模型 etotal=f(r, l, n) 受雷达设备误差、特征点空间分布,以及特征点数量的综合影响,由于求解单应性变换矩阵最少需要 4 组点对并且不能共线,所以采用控制变量的方式研究特征点数为 4 对情况下,不同空间构型对标定误差的影响。定义两种主要的空间构型如图 6、图 7所示。
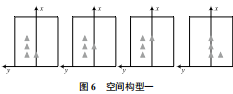
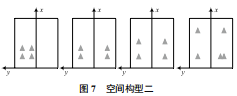
由于 4 点不共线主要考虑空间构型一与空间构型二这两种位置分布,其他位置分布可以通过整体旋转、平移与这两种空间构型进行等效。实验采集一定组数的空间构型一与空间构型二的定标物雷达坐标数据 (xr, yr),通对标定误差进行计算,将数据记录在表 3 与表 4。


两种构型标定误差如图 8 所示。
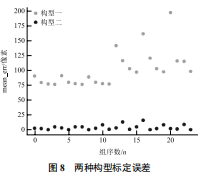
由图中的构型数据与误差的关系可知,空间构型二的特征点位置分布比构型一所示的空间分布标定误差更小。并且对表 4 中构型二数据进行分析可知,对于空间构型二的位置分布,当 4 个点空间差异越大即 4 个点在横向和纵向距离增大时标定误差会下降。
2.2.3 特征点数量实验分析
通过实验分析了空间构型对单应性变换标定误差的影响,证明了空间构型二比空间构型一的标定误差小,本节选择空间构型二作为特征点分布,保持构型不变的情况下研究特征点数量对单应性标定误差的影响。特征点位置实验数据(xr, yr) 为(11.2,2.5),(14,2.5),(18.2,-4.7),(24,-4.7)(17,2.5),(30,-4.7),(20,2.5),(36,-4.7),表 5 为不同特征点数量的标定误差数据。
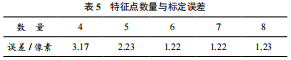
通过表中的数据可以看出,在同一种空间构型下,随着特征点数量单应性标定误差逐渐下降,当点数增加到 6 个点时,标定误差已经基本不发生变化。所以在标定时选择 6 个点较为合适。
3 结 语
本文研究了毫米波雷达与摄像头单应性变换标定方法中误差因素对单应性变换标定精度的影响。建立了误差模型并分别对毫米波雷达设备误差、特征点空间位置构型、特征点数量这三个因素对标定精度的影响进行了实验分析。结果表明,文中的空间构型二特征点位置分布的标定误差较小,并且在空间构型二下,特征点数量选择 6 点标定误差可达到最小并且基本不再变化。本文的结果为后续毫米波雷达与摄像头标定实验方案的设计提供了基础,具有一定的研究意义。
审核编辑:汤梓红
-
以摄像头和毫米波雷达为技术核心的自动紧急制动2016-11-07 4310
-
摄像头、毫米波雷达以及车身控制器剖析2016-12-09 4785
-
教你设计单芯片毫米波雷达传感器2018-06-12 6837
-
毫米波雷达方案对比2018-08-04 12229
-
车载毫米波雷达的技术原理与发展2019-05-10 5894
-
汽车毫米波雷达传感器的性能一致性2019-07-29 5998
-
主流厂牌的毫米波雷达芯片有哪些?2019-09-16 9775
-
毫米波雷达(一)2019-12-16 14676
-
毫米波雷达感知技术搭建车路协同系统的可行性2020-07-01 9142
-
毫米波/激光/超声波雷达的区别 精选资料推荐2021-07-27 4512
-
毫米波雷达的特点是什么2021-07-30 7182
-
雷达传感器模块,智能存在感应方案,毫米波雷达工作原理2021-10-28 3887
-
ADAS系统无人驾驶的眼睛毫米波雷达2023-04-18 2085
-
从国内AEB的落地解读摄像头与毫米波雷达的融合技术2018-09-04 3866
-
自动驾驶-毫米波雷达与摄像头.zip2023-01-13 516
全部0条评论

快来发表一下你的评论吧 !

