降低OFDM系统PAPR的LDPCSS⁃GA方法

摘  要：为了降低面向 5G 的正交频分复用系统的峰均功率比和计算复杂度，采用 5G 通信领域中的低密度奇偶校验码信道编码方案，通过部分传输序列改进后的循环移位序列方法与低密度奇偶校验码联合方法进行编码，称为 LDPCSS 码，根据导出 LDPCSS 码的奇偶校验矩阵，使用置信度传播算法进行译码。为了进一步降低 LDPCSS 码的延迟和搜索复杂度，提出基于遗传算法的 LDPCSS方法，称为 LDPCSS⁃GA 方法。通过仿真与现有方法进行比较分析，结果表明，所采用的方法降低了BP译码器的译码复杂度和延迟，同时降低系统的 PAPR 和计算复杂度，还提升了误码率性能。

0 引 言

正交频分复用（OFDM）采用多载波调制技术，具有高数据传输速率和抗窄带干扰能力，与其他多载波技术相比，其带宽利用率高，可增加系统容量还能提供可靠的传输，能适应第五代（5G）宽带无线通信网络[1]。但OFDM 系 统 的 主 要 缺 点 之 一 在 于 高 峰 均 功 率 比（PAPR），因 为 信 号 通 过 某 些 非 线 性 设 备 传 播 时 ，高PAPR 可能会导致带内失真和带外辐射，从而导致系统误码率性能下降[2]。

目前，研究降低 OFDM 系统 PAPR 的方法有很多，大致可分为两类：一类是信号失真技术[3]，如削波、滤波和星座扩展等。削波技术是将信号削波到预定的阈值以下，对于 OFDM 系统，很容易产生带内失真和误码率升高，星座扩展是无失真技术，但会增加发射信号的能量。第二类包括信号加扰技术，如选择性映射（SLM）[4]是在多信号表示方法的基础上，具有与编码、星座扩展相似的特性，且需要发送边信息，会产生较高的计算复杂度和降低带宽效率。部分传输序列（PTS）[5]是 PAPR降低研究最广泛的技术，也是无失真的一种方法。由于 PTS 方法将相位因子信息作为辅助信息发送到接收机，会导致传输效率降低且增加了系统复杂性，文献[6⁃7]采用 GA 遗传算法对旋转因子进行优化，PAPR 性能降低了，但在接收机上需要附加相关技术来恢复发送的 OFDM 信号。

文献[8]采用循环移位序列（CSS）方法，CSS 方法是从 PTS 方法发展而来的，它将 OFDM 信号子序列循环移位并组合后替代 OFDM 信号序列，通过循环移位序列而不是将旋转因子乘以 OFDM 信号子序列，不管从 PAPR降低还是系统性能上，CSS方法比 PTS方法更好。

OFDM 系统另外一个主要缺点是在衰落环境中的BER 性能差，导致接收器不可能无错误地检测到所有子载波。为了减小衰落的影响，文献[9]采用 LDPC 编码技术实现 OFDM 系统。文献[10]将 Turbo 编码技术应用到OFDM 系统中，虽然 Turbo码在编码过程中比 LDPC 码简单，但在译码时比 LDPC 码复杂得多，而 LDPC 码具有较强的纠错能力和抗突发差错。文献[11]采用遗传算法（GA）优化 LDPC 码，GA 的特点在于能解决高维优化问题，不仅能找到局部最小值，且选择恰当的参数能很快收敛并获得最优解，常用于人工智能、信道编码和 LDPC译码器等领域。

综上所述，本文提出了一种对 LDPC 码和 CSS 联合编码的方法（称为 LDPCSS 码），即将 CSS 和 LDPC 码作为前期编码阶段，然后导出 LDPC⁃CSS 码的奇偶校验矩阵，通过奇偶校验矩阵，使用置信度传播算法（BP）和GA 算法进行联合译码。

1 LDPCSS联合方法的编译码

1.1 OFDM 系统的 PAPR 计算方法

OFDM 信号由多个独立调制的子载波组成，当相互叠加时，会产生较大的 PAPR，当 N 个信号以相同相位叠加时，所产生的峰值功率是平均功率的 N 倍，在时间间隔 τ中传输的信号 x ( t )的 PAPR 定义为：

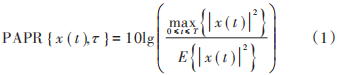
式中：max { ⋅ }表示峰值信号功率；E { ⋅ }表示平均信号功率。为了计算更精确的 PAPR 值，应考虑更多符号，否则可能会省略一些峰值，从而导致 PAPR 值错误，可通过对 x ( t ) 进行过采样来解决，用互补累计分布函数（CCDF）定义峰均值超过某一门限值的概率：

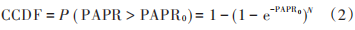
式中 PAPR0表示某个限幅电平的 PAPR 值。

1.2 基于 LDPCSS⁃GA 的 OFDM 系统

在 LDPCSS⁃GA 的 OFDM 系统中（如图 1所示），一个LDPC 码字通过 PSK 调制和 QAM 映射到 OFDM 子载波上，经随机交织器后，将行向量 R表示的 LDPC 码字映射到子载波数为 N 的一个 OFDM 数据块上。然后将 X 划分为 V 个不相交的子块，经 IFFT 变换后得到时域序列。

不妨令 N和 V为 2的整数幂且分割满足条件 Xv ( k ) = 0或∑v=1VXv = X，k = 1, 2,⋯,N，则 CSS 候选数据子块 XCSS 表示第 V 个 OFDM 信号系列经循环下移与求和组合后得到第 y（1 ≤ y ≤ Y）个 OFDM 序列[12]为：

式中，xyv 表示xv通过整数μyv循环左移，即：

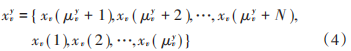
式中：μyv表示偏移值；对于第y 个 OFDM序列满足：-μy ={ μy1, μy2,⋯, μyV}，-μy 表示第y 个备选OFDM信号序列的偏移值集合。

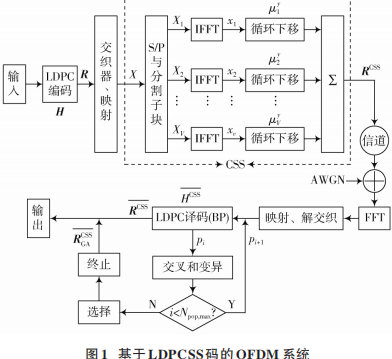
由文献[12]可知，循环移位操作不会破坏输入符号序列之间的正交性，因时域中的循环移位等效于在频域中乘以相应的线性相位矢量。因此，当获得校验矩阵 H后，可根据校验矩阵 H 进行编码，从而得到相应的码字R，Rv ( v = 1, 2,⋯, V ) 表示循环移位后的行向量，经 CSS处理后，原始的LDPC码字R被分割为V个向量，即R1，…，RV，长度为 N（vv = 1, 2,⋯, V），并得到相对应的行向量(RCSS) v，表示为( RCSS) 1，( RCSS) 2，…，( RCSS) V。根据 CSS和以上假设，则：

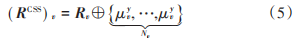
式中 ⊕ 表示模 2加法运算。

本文将 RCSS 作为等效传输码字，将 LDPCSS 码字定义为由等效传输码字和循环移位组成的码字。

定义 1：先前描述的 OFDM 系统的 LDPCSS 码是具有以下码字的分组码，它的矢量表示为：

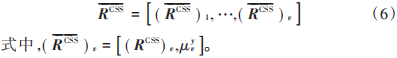
根据文献[11]和式（3）、式（4），不妨设 y=2，则由两个偏移集 μˉ 1 和 μˉ 2 生成的备选序列由 ( RCSS) 1 和 ( RCSS) 2 表示，不失一般性，令( RCSS) 1 为不受 CSS 处理影响的行向量，由全零偏移集 μˉ 1 = { 0, 0,⋯, 0 }生成为：

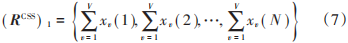
同理，( RCSS) 2通过偏移集μˉ 2 = { μ21 , μ22 ,⋯, μ2V}生成为：

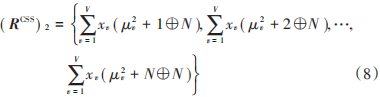
1.3 PAPR 减小和 LDPCSS⁃GA 算法

本文减小系统 PAPR 值采用文献[12]的交织分区以及制定的标准 2生成的偏移集，如果满足：

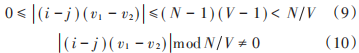
其中：1 ≤ v1 ≠ v2 ≤ V，1 ≤ i ≠ j ≤ N，N 表示子载波数，V 表示子块数，且满足 N = WV - 1，W 为旋转因子数。考虑 LDPCSS 码的优化问题，在设计过程中，尽量降低系统 PAPR、误码率和复杂度，因此应用了遗传算法。遗传算法是一种常用的函数优化方法，它具有全局搜索能力，可获得最佳或更好的近似解。LDPCSS⁃GA 算法基本思想如下：

1）初始化：种群大小 p，编码率 Rc，码长 N，设置最大迭代次数 N max, pop。2）for i = 1, 2,⋯,N max, pop do

3）更新种群：将父代向量 H1 的第一行与父代向量H2 的第二行相结合生成下一代向量 H1，交叉率 pc = 1。将下一代的随机位置上 0 → 1生成为 H1a，突变率 pm = 1。为了恢复编码率 Rc，对产生的后代向量 H1a进行突变，产生向量 H1b作用于群体，并更新种群。

4）计算适应度函数：LDPC译码是基于Tanner图的消息传递迭代译码，采用置信传播译码算法（BP）沿Tanner图的边传递概率值，对位节点的判据采用其概率值组合。

5）计算 BER：初始化 BER 并对每次输入-----RCSS 的种群大小进行更新，采用 BP算法并更新 BER。

6）end for

7）选择最优向量-----RCSSGA 输出。

8）结束

本文将每次更新的最佳-----RCSS 向量作为新种群的成员，虽然收敛速度减慢，但能确保收敛到局部最优值，并通过不断进化保证目标函数的单调性，以便观察候选解。

2 仿真分析

通过概率密度演化方法[13]得到最大变量节点度分布，并构造和优化奇偶校验矩阵H，仿真中发射机不发送循环移位序列，接收机采用 BP算法。

图 2显示了不同方法降低系统PAPR的性能比较，相关的参数设置见表1。在 CCDF 为10-3时，本文采用的LDPCSS联合方法降低系统PAPR 约 5.7 dB，相比文献[9]方法降低约0.1 dB，且明显优于其他方法。

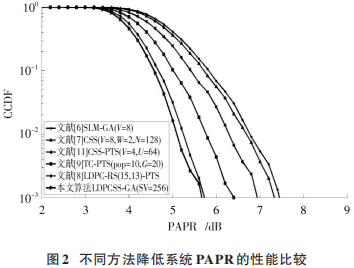
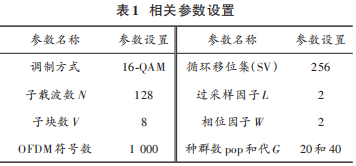
图 3显示了不同方法的 BER性能，为了与文献[9⁃10]的BER性能比较，设置码率为1 2，约束长度为4，输入回退为3，N =512，在AWGN 信道中采用16QAM，可以看出，本文采用的方法在传输信号的 PAPR 值较大时，BER 性能下降很小，随着子载波和星座数增加，BER 性能明显优于文献[9⁃10]方法。

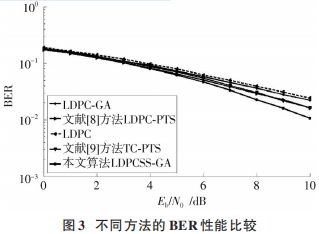
图 4 显示了原始 OFDM 信号和采用 CSS 处理后 ，当子载波数 N=8，16，32 和 64，CCDF=10-3 时，经过 CSS处理后的 PAPR 分别降低了约 6.2 dB，6.6 dB，7.1 dB 和7.7 dB。

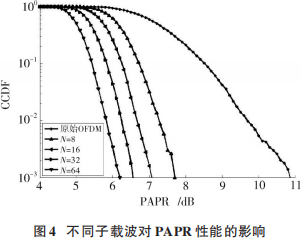
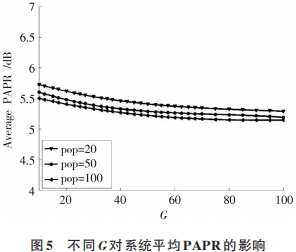
图 5 显示采用 LDPCSS⁃GA 方法的 PAPR 平均值分析，其中种群大小设置为 20，50和 100，G 在 10~100之间取值，可以看出种群数在 20~100 时，平均 PAPR 的值相差 0.2 dB，显然种群数为 20比较合理。

3 结 语

本文提出了一种基于 LDPCSS 码的奇偶校验矩阵，并使用 BP 算法对 LDPC 码字和循环移位因子进行联合译码，通过 GA 算法不仅降低了 OFDM 系统的 PAPR，且经过优化后的 LDPC 码，既降低了 BP译码器的译码复杂度和延迟（因为不需要传输辅助信息即循环移位因子，也不需要在译码前对其进行估计），又在误码率性能方面得到了提升。仿真结果表明，本文所采用的 LDPCSS⁃GA 方法与其他方法比较，有效降低了 PAPR 和计算复杂度。由于需要进一步降低了 PAPR，因此，在未来研究中，如何提高译码的收敛速度且不降低纠错能力仍是一项重要的工作。

审核编辑：汤梓红