寄生电感怎么来的

Q值又叫品质因数，是衡量一个谐振回路或线圈的品质的重要参数。因为是个比值，所以是个不名数，只有数值，没有单位。

如何计算？对谐振回路而言，Q值等于这个谐振回路线圈的电感量（亨利，H），除以：电容器电容量（法拉，F）乘以回路电阻（欧姆，Ω）的乘积。也就是说，谐振回路的线圈电感量越大、电阻和电容越小，谐振回路的Q值越高。
对线圈而言，Q值等于这个线圈的电感量，除以这个线圈的电阻值。也就是说，线圈要想提高Q值，可以换粗线绕（低频）、或使用多股线绕（中频中波段）、或蜂房绕法（减小分布电容）、或用镀银线间绕（高频短波段）、或加磁芯（用长磁棒），都可以提高Q值。

提高Q值有何好处呢？因为线圈是谐振回路的一个组成部分，所以我们不用谈线圈，只谈谐振回路就可以了。Q值高了，谐振回路的选频能力就强，收信机的灵敏度就高（可收到原来听不到的远地电台），选择性就好（不串音），性能就提高了。

可谐振回路的Q值也不是越高越好，因为Q值高，选频的峰虽然高了，但通带却变窄了，同时稳定性变差，调好的电台一松手就跑了。通带变窄对中波短波以听新闻语言为主的电台当然无所谓了，这些电台的频宽只有9千赫（原来是10千赫，1978年改为中波段国际标准9千赫，短波段仍然保持10千赫）；但对听音乐为主的调频电台和电视台就不行了，调频电台的带宽250千赫，电视台信号带宽8000千赫，再使用原来的电路就不行了，增加带宽的办法有两个：较好的方法是，使用多个不同频率的调谐回路共同组成一个宽频带，这个方法在保证灵敏度和选择性不变的前提下可以增加带宽，缺点是线路复杂，要使用多级放大，简单的方法是，向谐振回路上并联一个电阻，并联的这个电阻阻值越小，带宽增加的越多，这个方法的优点是：简单。缺点是：放大量显著变小，灵敏度和选择性明显变劣。

关于谐振回路Q值的讨论：线圈的Q值较好理解，同样的电感量，电阻越小，震荡起来损耗就越小，Q值肯定要高啦。但是对于谐振回路，为什么又把电容量弄到分母上，电容量越大反而Q值越低呀？电容也储存电能呀，真是令人费解。

真实的情况是这样的：谐振回路对某一频率的交流电谐振是有条件的，就是线圈的电感量与电容器的电容量的乘积必须为一个固定值，当线圈对这个交流电的感抗与电容器对这个交流电的容抗一样大时，因为二者方向相反，可以互抵，这个谐振回路就对这个频率的交流电谐振了。有两种方案可做比较：大电感配小电容，或小电感配大电容（因为要乘积为固定值）。第一种方案电路中电压高，电流小，因为电感量大，所以同样的电流能感应出高电压，但电容量小存电量小形不成大电流，属于高压小电流方案；第二种方案电路中电压低，电流大，因为电感量小所以同样的电流只能感应出不高的电压，但电容量大存电量多可以形成大电流，属于低压大电流方案。这样就很清楚了，震荡是电流在线圈与电容器之间来回跑，与高压输电原理相同，高压小电流方案损耗必然小，Q值肯定高啦。

 

从理论上分析，Q值等于谐振回路的电抗的绝对值与电阻的比值。电抗越大、电阻越小谐振回路的Q值越高。线圈的感抗是和电感量成正比的，而电容器的容抗却是和电容量成反比的，使用大电感量与小电容量组合成的谐振回路，可形成较大的电抗，是大感抗对大容抗互抵，从而形成高Q值。而使用小电感量与大电容量组合成的谐振回路，却无法形成较大的电抗，是小感抗对小容抗互抵，从而Q值很低。

引言

寄生电感这个字眼就经常出现，特别是引线电感。我们解释一些问题的时候都是直接套用的，默认它的存在。可实际上是，我在很长一段时间内并不理解它到底是怎么来的，因为我印象中电感都是线圈，而直导线并不是。直到之前不久我才思索了一番，算是有一些了解，也写了下面一篇文章。

寄生电感怎么来的

最近一直在看电感和磁珠的内容，也有看LC滤波器，自然会有LC谐振的问题。LC串联谐振，单独拿出来说的话，可能会觉得太简单了，这有啥好说的。自然是因为实际应用中会出现各种各样的场景，尽管都是谐振，但是表现各不相同。

先来思考下这么几个问题：

电路中不必要的LC串联谐振要绝对杜绝吗？

MOS管G极经常串联一个小电阻，说是可以抑制振荡，啥原理呢？这个电阻阻值怎么取呢？

电源上面加上磁珠，结果纹波变大了，只能换0Ω电阻来解决吗？有没有其它的解决方法？

这几个问题，如果你明白了LC串联谐振的分析方法，那么自然都不在话下了。

LC串联谐振电路

尽管LC串联谐振电路非常简单，我们还是来看下，这样一步一步深入会更好的理解。

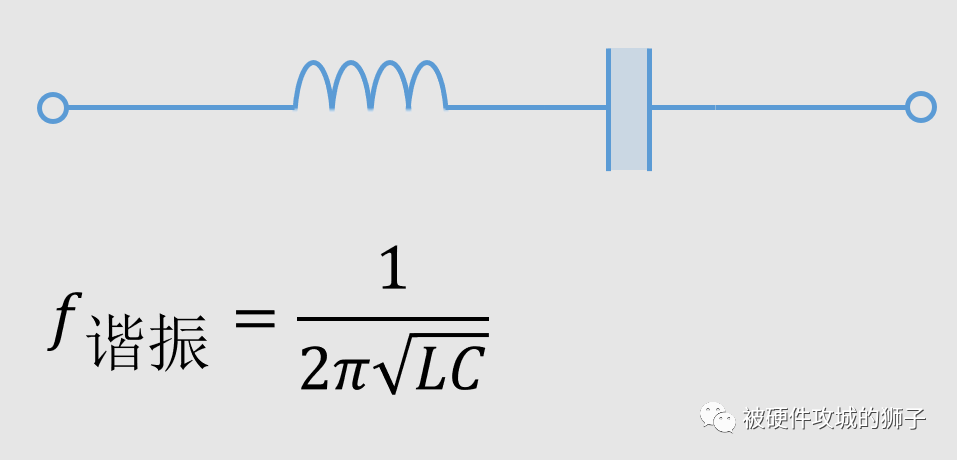
一个电感和一个电容串联，在某个特定的频率，就会发生谐振，这个频率就是谐振频率。串联谐振电路有如下特点：

谐振时整个电路阻抗呈电阻性，阻抗最小，电流达到最大；

谐振时电感和电容两端的电压达到最大。

上面这些理论都是非常基础的，就不赘述。实际电路的场景要远比这个要复杂，搞清楚那些才是我们的目的。那么我们下面就来结合具体的场景。

LC滤波器

LC滤波器经常用，但有一个比较坑的问题就是，有时候使用LC滤波器之后，效果反而更差了，还不如不用。

原因我们当然可以说是在噪声在此处谐振啦，噪声被放大了之类的。曾经的我也会这么说原因，不过并不是真的明白，对于这种会起反效果的东西，我会惧怕，会担心它出问题。这种惧怕，来源于对未知的恐惧，因为没有懂。现在下面来具体分析下

首先，我们需要明白，噪声是如何被放大的？也就是说输出比输入幅度要大？

先来看最简单的模型，也就是理想器件模型的情况。

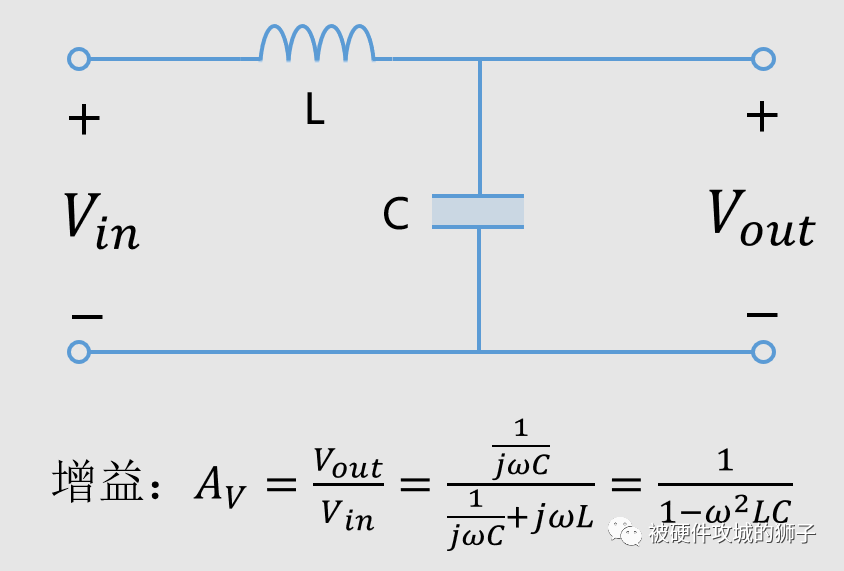
我们列出输出与输入的比值，也就是增益，如果增益大于1，那么说明被放大了。很容易列出增益的公式，我们画下这个曲线。

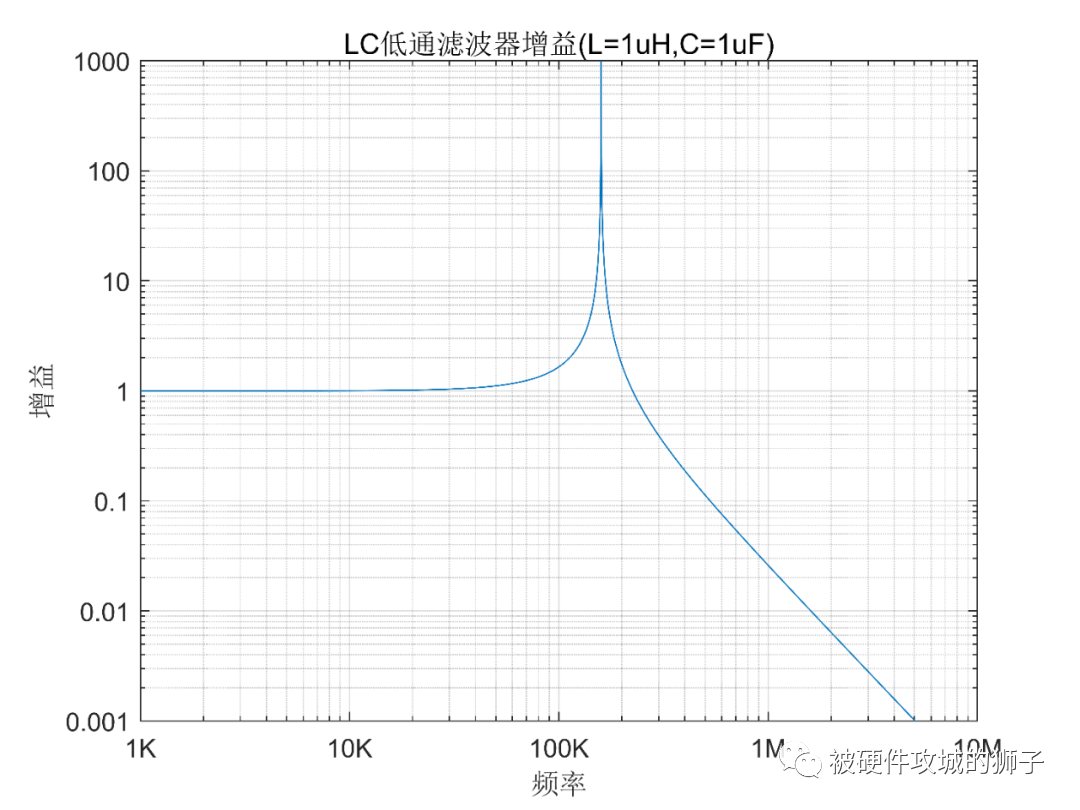
上图的曲线，是1uH电感，1uF电容的增益。可以看到，在低频时，增益基本就是1，也就是不放大不衰减。而在谐振频率处，有一个非常高的尖峰，因为这里设定的器件为理想器件，所理论上尖峰为穷大，谐振频率旁边的增益也是非常高的，而在频率比较高的时候，随着频率的升高，增益下降，也就是衰减了输入信号。

如果我们能把谐振频率处的增益降到0．707左右，那就是完美的低通滤波器了。很显然，电感和电容都是非耗能器件，没有电阻器件的引入，在谐振频率处，增益总是等于无穷大的。我们从增益Av的公式就可以得出来，因为谐振频率时的分母为0。

幸运的是，我们的滤波电路总是要接负载的，我们把信号滤波之后总是要给负载用的，接入了负载，那增益又不一样了。

不同负载的LC滤波器

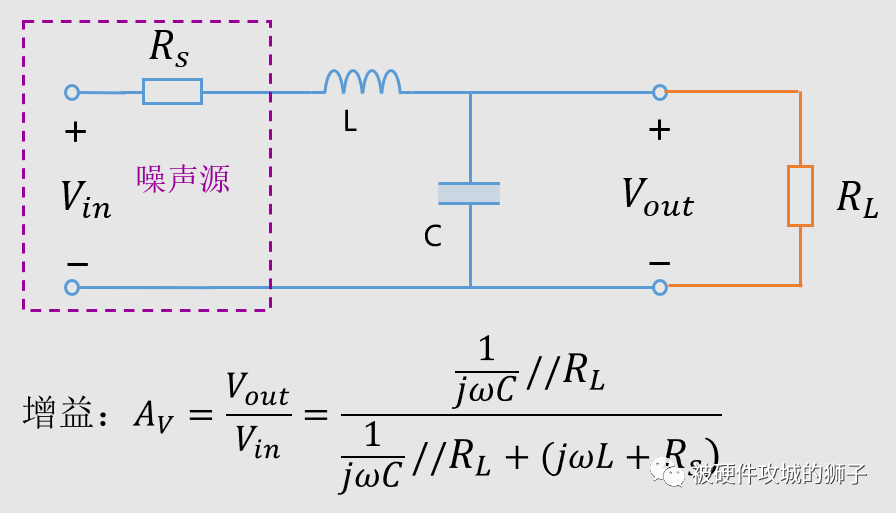
现实中的电路各种各样，负载的阻抗也就差别很大了，下面是加入负载的模型。

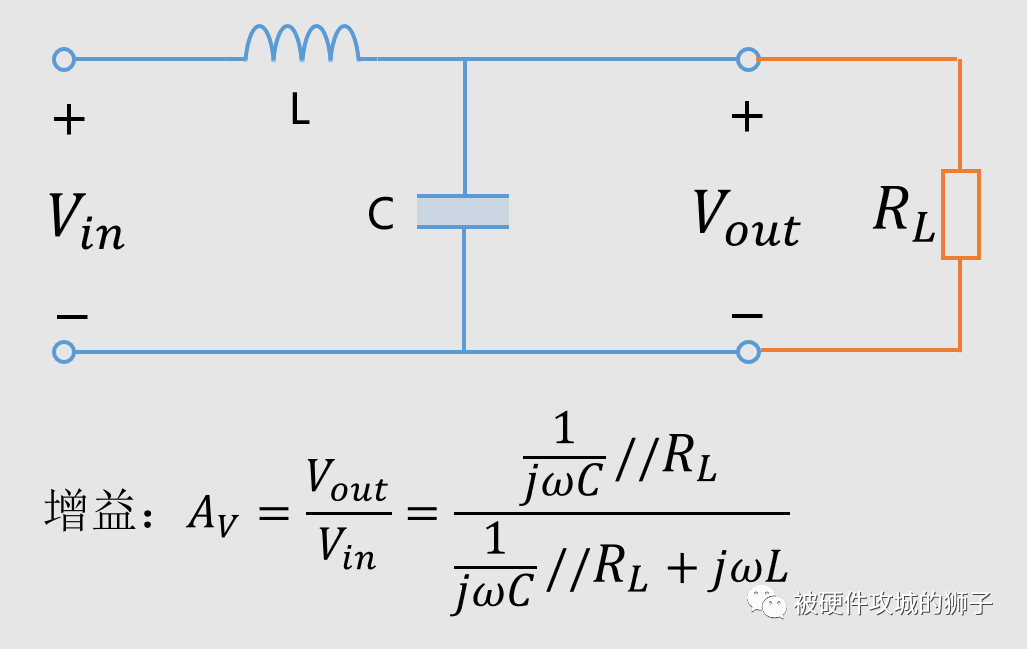
我们看看负载是1Ω，10Ω，100Ω的增益曲线，如下图：

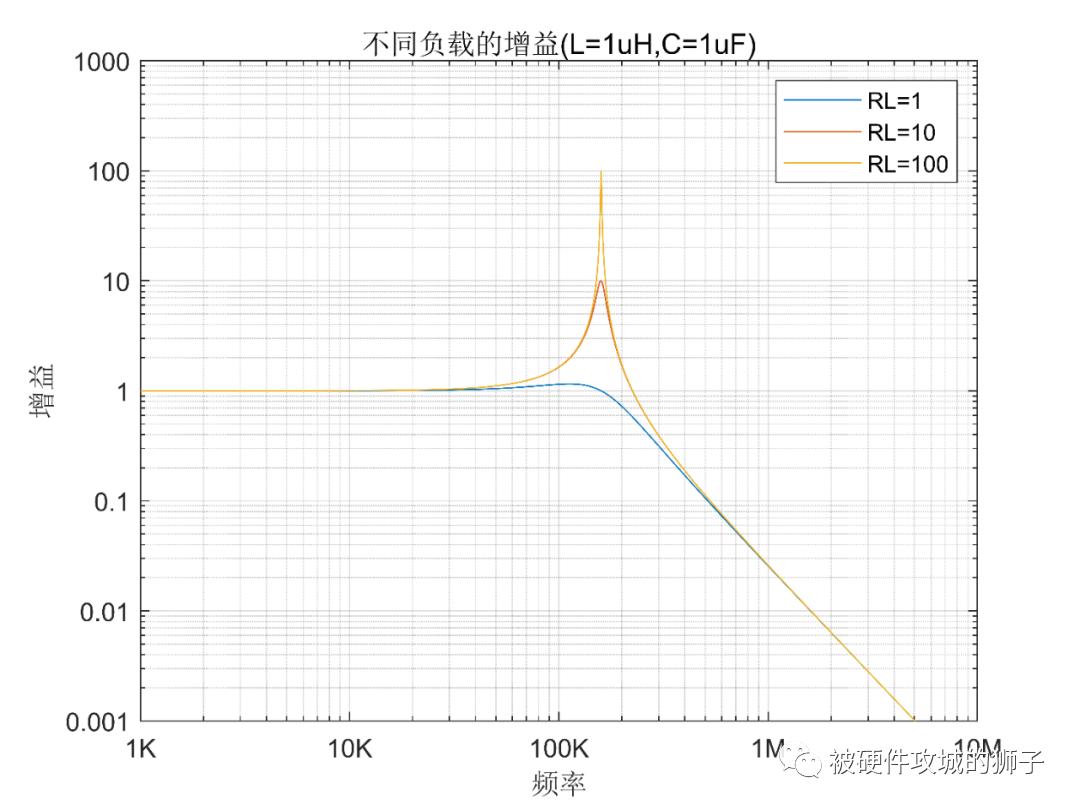
我们可以看到，负载电阻越小，谐振处的增益越小，谐振引起的噪声变大越不会发生。当然了，实际电路中的负载各种各样，有低阻的，有高阻的。相对来说，低阻负载的更不容易发生加入滤波器效果更差的事情。因此，如果你发现同样的LC滤波器，加入不同的电路，有的效果好，有的效果变差，很有可能就是因为负载的不同。

所以说，负载阻抗越低，越不容易产生尖峰，也就是说不容易恶化。

噪声源内阻的影响

除了负载阻抗的影响，还有噪声源内阻的影响，实际的噪声信号肯定是有一定的内阻的。根据内阻的不同，我们构建下面的模型，加入内阻的参量。

分别画出Rs＝0．1Ω，Rs＝1Ω，Rs＝10Ω的情况，为了排除负载电阻的影响，宁其为高阻态，统一RL＝1MΩ。

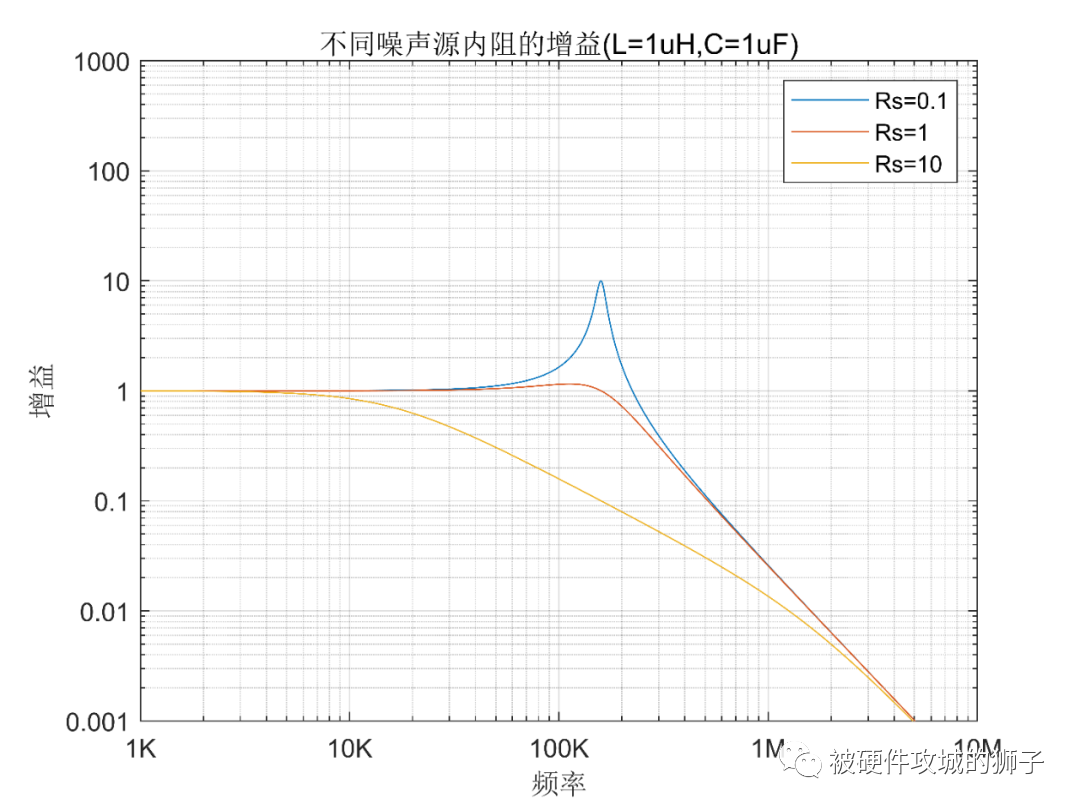
可以看到，内阻越大，越不容易产生尖峰，也就是说不容易恶化，反之，内阻越小，越容易恶化。

L、C的值的影响

除了内阻和负载大小，电感和电容值的大小有没有影响呢？

电容变化：电容分别为1uF，10uF，100uF，内阻，负载，电感都为Rs＝0．1，RL＝1MΩ，L＝1uH。

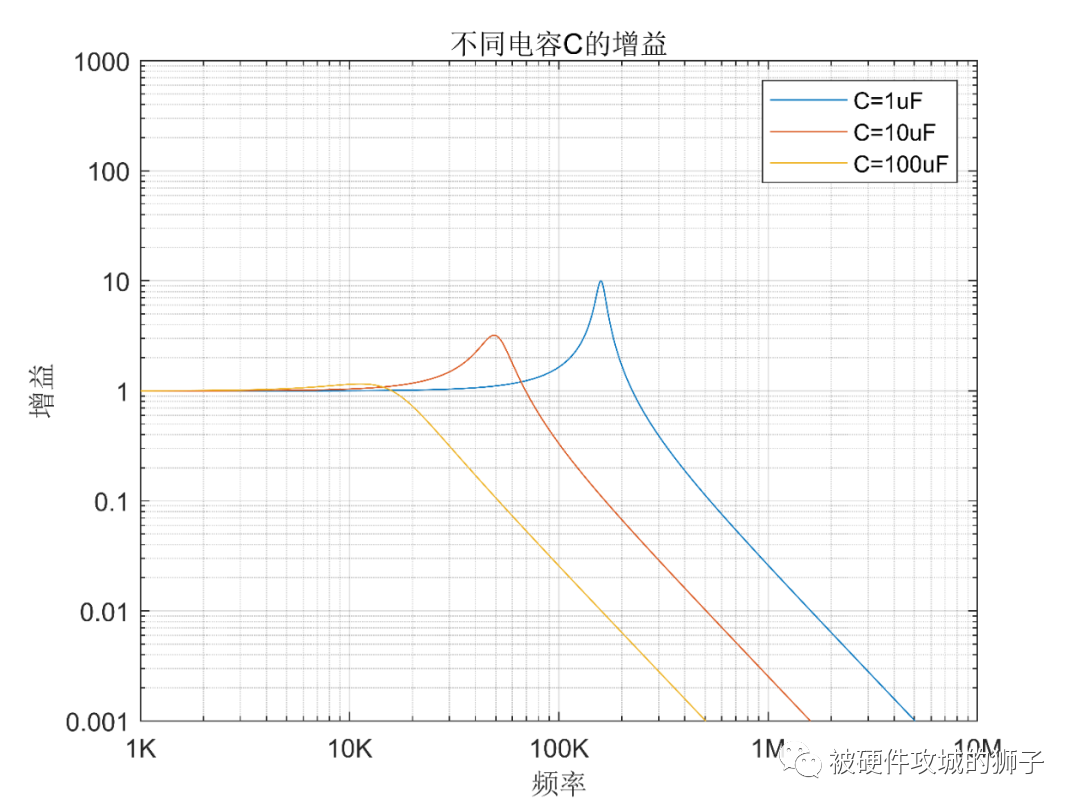
可以看到，电容增大，尖峰变小，也就是说，在遇到谐振引起噪声增大的情况，可以尝试增大电容是可以降低噪声。不过需要注意，尖峰变小，只是说最高点变小了，但是引起了谐振频率降低，新的谐振点可能还是要比原来的增益更高，也就是说如果噪声正好是这个频率段，那么改变之后效果变更差了。当然了，如果我们加更大的电容，即使是谐振点都没有放大作用，比如如果电容加到100uF，整个频段基本都没有放大作用了。

实际电路具体加到多大的电容，完全不会出现尖峰呢？这个跟信号源内阻Rs，负载阻抗RL，电感值L都有关系。实际上，如果内阻Rs从0．1提升到1，电容不用增大到100uF，即使是原来的1uf也不会有尖峰，曲线就不画了。

电感变化：电感分别为0．01uH，0．1uH，1uH，内阻，负载，电容都为Rs＝0．1，RL＝1MΩ，C＝1uF

可以看到，减小电感，可以降低尖峰的高度。我们如果继续减小电感到0．01uH，尖峰也会消失。同样的，电感变化会造成谐振频率移动，具体是使噪声变大还是变小也是要依情况而定，与内阻，负载，电容都有关系。

总的来说，大部分电路增大电容，或者减小电感，都可以降低尖峰。如果LC滤波器用于电源滤波发生噪声变大，可以增大电容，或者减少电感。

这里之所以说大部分电路，是因为如果满足一定的Rs，RL的条件，可能结果是相反的，这个可以自己修改Matlab代码（后文分享出来）里面的参量，执行下就知道了。

MOS管G极串联电阻如何抑制谐振

有了以上的基础，我们来看实际的问题：MOS管G极串联电阻如何抑制谐振？

这个问题，我们首先要明白，问题是如何产生的，即为什么会振荡？其实通过前面的铺垫，也就很明白了。

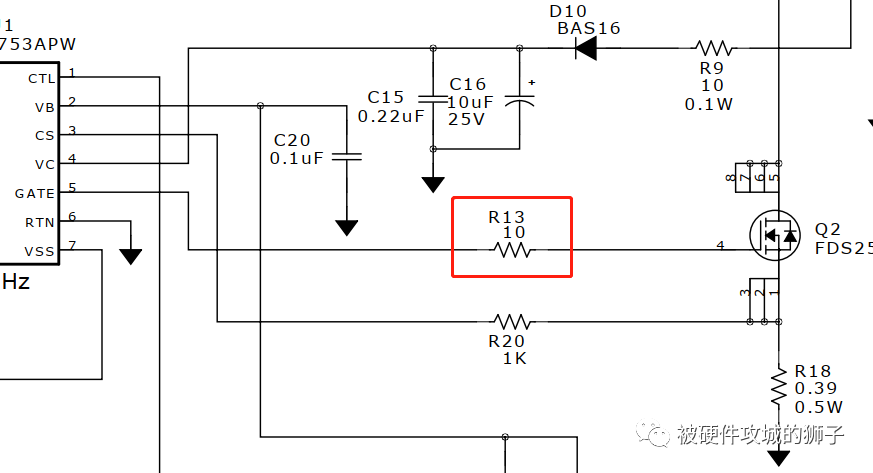
这个是典型的MOS管驱动电路，串联了10Ω电阻。

尽管从电路图上看去，上面既没有电感，也没有电容。但实际上是，我们PCB总要将线从驱动芯片拉到MOS管，我查了一下，线宽12mil，长度10mm的走线寄生电感是9．17nH。实际电路中10mm走线太正常了，所以寄生电感肯定是存在的。

电感有了，电容呢？功率MOS管都有输入电容存在，并且还不小，小的几百pF，大点的几nF。我们只是为了说明道理，那取电容1nF吧。

一般来说，左边驱动管子发出开关信号，它的内阻一般不会很低，尽管现在不知道它到底是多大，那就按照比较恶劣的情况来看，就让Rs＝0．1Ω。

那么负载电阻是多大呢？负载是MOS管，那阻抗就很大了，就取RL＝1MΩ。

看看现在的等效电路：

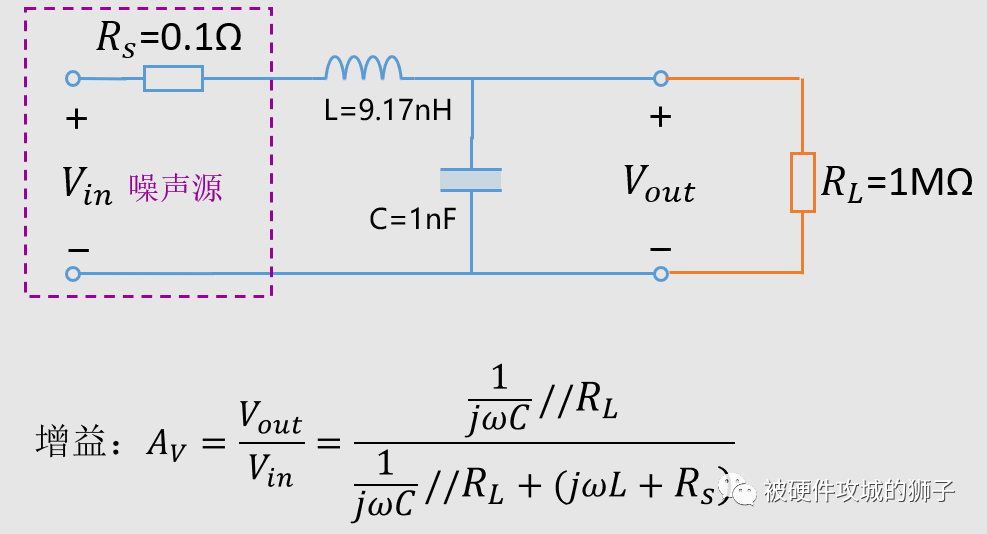
从前面内容知道，源内阻越小，负载阻抗越大，就越容易产生谐振尖峰。我们画出此时曲线。

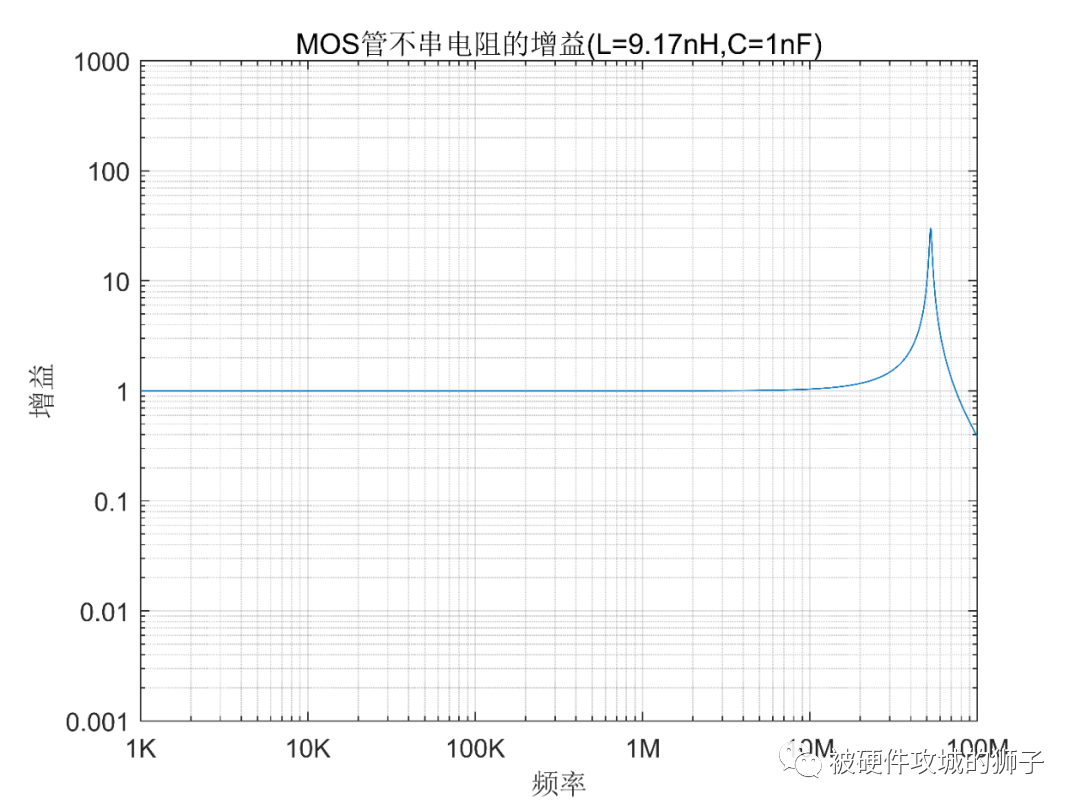
可以看到，谐振频率52Mhz处增益达到了好几十倍。而MOS管驱动信号可以看作是一个阶跃信号，频率分量非常丰富，肯定有52Mhz附近的频率。

所以说确实会发生谐振。

现在分别串联1Ω，10Ω，100Ω电阻，这个电阻可以等效到内阻里面去，相当于等效电路变成了Rs＝1．1Ω，Rs＝10．1Ω，Rs＝100．1Ω，其它参数不变。我们再看看曲线。

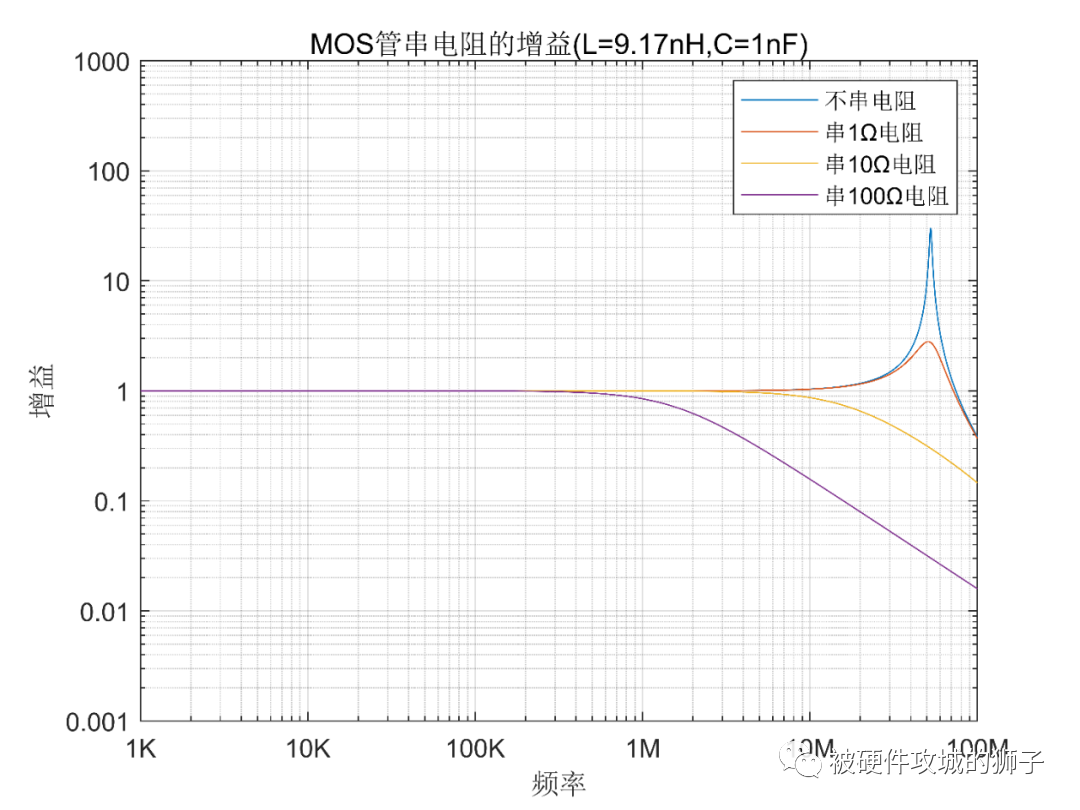
可以看到，串联1Ω电阻，还是放大，最大到3倍，说明电阻稍小。而10Ω电阻就能完全消除振荡了。100Ω电阻也能完全消除振荡，但是其截止频率更低，会造成驱动信号的高频分量丢失，最终上升沿变缓，也就是MOS管开启的时间变长。

相信到这里，对于这个串联电阻的作用，已经怎么取值应该就比较清楚了。G极走线越长，寄生电感越大，越容易引起问题，电阻就要选得更大些。

审核编辑 ：李倩