

RC无源带通滤波器电路设计方案
模拟技术
描述
一般情况下,可以说带通滤波器是低通滤波器和高通滤波器的组合。过滤器本身的名称表明,它只允许某个特点频段的频率通过,并阻止所有其它的频率。
例如,在音频应用中,有时只需要通过一定范围的频率,该频率范围不会以0Hz开始,也不会以非常高的频率结束,但这些频率都在一定范围内,无论是宽还是窄,这些频带通常称之为带宽。
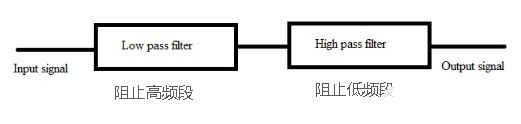
RC无源带通滤波器
带通滤波器由无源低通滤波器和无源高通滤波器级联而成,该布置将提供仅通过特定频率的选择性滤波器。所以,这种新型RC滤波器电路能够通过窄范围的频率或宽范围的频率。
这种窄或宽范围的频率通过范围将取决于无源低通和高通滤波器级联的方式,上限和下限截止频率取决于滤波器设计。其实,带通滤波器看起来就像频率选择性滤波器。
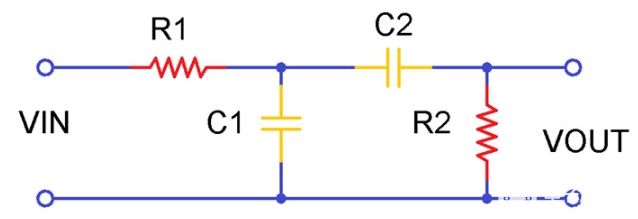
上图显示了典型的带通滤波器电路。给定的输入是正弦信号。低通和高通组合的特性为我们提供了带通滤波器。通过串联一组RC元件和并联另一组RC元件,该电路的行为就像一个带通滤波器。
以上是一个二阶滤波器,因为电路有两个电抗元件。一个电容属于低通滤波器,二另一个电容属于高通滤波器。在输入信号没有任何变化的情况下,该带通滤波器将通过一定范围的频率,而且该滤波器不会在信号中产生任何额外的噪声。
电路的截止频率可以计算如下:
f C = 1/(2πRC)
通过调整高通和低通滤波器的截止频率,可以获得适合带通滤波器的通带宽度。
由于带通滤波器通过一个频带,所以该滤波器包含两个截止频率,较低的截止频率“fL”和较高的截止频率“fH ”。因此,通过滤波器的频率范围称为滤波器的带宽。一般来说,电路的带宽可以通过频率“f H和fL ”来计算,公式如下:
BW=fH – fL
其中,“fH ”是高通滤波器的截止频率,“fL ”是低通滤波器的截止频率。“BW”是滤波器的带宽。带通滤波器将通过高于高通滤波器截止频率和低于低通滤波器截止频率的频率。
以上内容表明低通滤波器的截止频率必须高于高通滤波器的截止频率。
使用R、L和C分量的带通滤波器
使用电感、电容和电阻的带通滤波器电路设计如下。
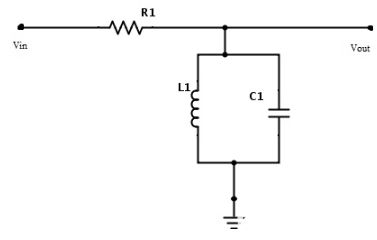
带通滤波器的中心频率也称为“谐振峰”,可以使用以下等式表示:
fc=1/2π√(LC)
其中L=单位为亨利 (H) 的电感器的电感、C=单位为法拉 (F) 的电容器的电容。
其实,也可以设计带电感器的带通滤波器,但的,由于电容器的高电抗,带RC元件的带通滤波器设计比RL电路更具优势。
频率响应
RC带通滤波器的频率响应图如下所示:
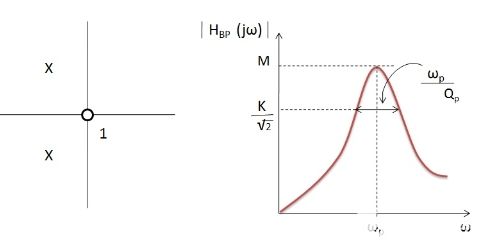
带通滤波器的频率响应由下式给出:
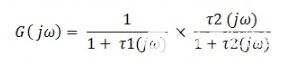
带通滤波器的传递函数如下所示:
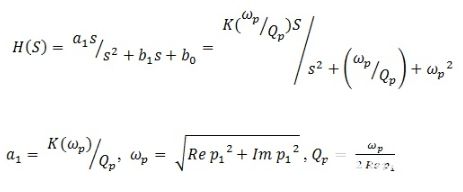
其中H(S)=s-plane的传递函数、τ1=R1C1、τ2=R2C2、ωp=磁极角频率=1/τ,τ=RC、K=1/Qp,Qp=品质因素。
另外,磁极角频率大约等于最大增益的频率。
带通滤波器的频率响应曲线如下图所示,由于电路的输入电抗,带通滤波器的理想特性和实际特性不同。
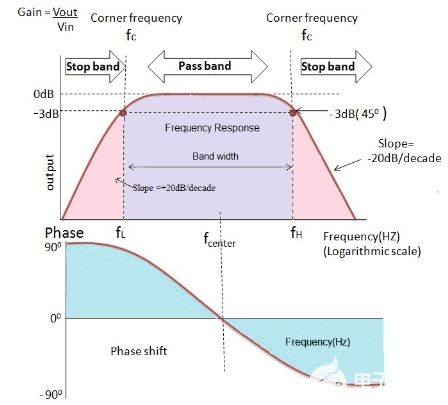
输入信号的增益可以通过取20log (Vout /Vin ) 来计算。根据电路的固有特性,该范围可能非常大。信号在低频下衰减,输出以每十倍频程+20dB或每倍频程6 dB的斜率增加,直到频率达到较低的截止频率“fL”。
在这个频率下,信号的增益达到1/√2=70.7%。
在截止频率fL之后,输出将以每十倍频-20dB的速率随着频率的增加而增加,并达到最大增益,并且该增益是恒定的,直到达到更高的截止频率“f_H”。在较高的截止频率之后,输出以-20dB/每十倍频或-6dB/每八倍频的斜率下降。
之前已经了解到,一阶滤波器的相移是90°。由于带通滤波器是二阶滤波器,因此相移是一阶滤波器的两倍,即180°。相位角会随着频率的增加而变化。在中心频率,输出和输入信号彼此同相。
低于谐振频率,输出信号超前于输入信号,高于谐振频率,输出信号滞后于输入信号。输入信号的幅度总是大于输出信号。为了增加电路的增益,电阻R1的值必须高于电阻R2。
中心频率
输出增益最大的“中心频率”或“谐振频率”可以通过计算上下截止频率的几何平均值来获得,公式如下:
fr2 =fHxfL,fr=√(fHxfL )
其中fr是谐振频率或中心频率、fH是上-3dB截止频率、fL是较低的-3dB截止频率。
典型示例
假设带通滤波器将允许从1kHz到30 kHz的频率通过,并且它包含10kΩ电阻器。通过考虑这些数值,可以计算电容器的电容。因为已经知道低通滤波器的截止频率值必须高于高通滤波器。所以高通滤波器的截止频率为1kHz,低通滤波器的截止频率为30kHz。
1、在高通滤波器阶段:
f=1kHz和电阻R=10kΩ,那么有:
C=1/(2πf LR) =1/(2*π*1000*1000) =15.8nF
2、在低通滤波器阶段
fH=30kHz和电阻R=10kΩ,那么有:
C=1/(2πf HR) =1/(2*π*30000*10000) =510pF
根据以上计算,高通滤波器所需的电容值为15.8 nF,低通滤波器电容值为510pF。
主要应用
用于发射器和接收器电路的无线通信介质。在发射器部分,该滤波器将通过唯一需要的信号并减少信号对其他站的干扰。在接收器部分,它将有助于将不需要的信号穿透到通道中。
用于优化接收器的信噪比。
用于激光雷达等光通信领域。
用于一些颜色过滤技术。
可用于EEG等医疗领域仪器。
在电话应用中,在DSL处分离电话和宽带信号。
总结
带通滤波器由低通和高通滤波器级联而成,它是二阶滤波器,因为它包含两个反应元素。在带通滤波器中,输出信号的增益总是小于输入信号。在中心频率下,输出信号是同相的,但低于中心频率时,输出信号超前相位,偏移+90°,高于中心频率时,输出信号将相位滞后,相移为-90°。
带通滤波器的实际特性与理想特性略有不同,这种变化主要是由于高通滤波器与低通滤波器的级联。另外,滤波器的品质因数取决于电阻值R1。如果R1低,则品质因数低,如果R1值高,则品质因数高。
-
RC无源带通滤波器的工作原理与特性2024-05-24 4587
-
滤波电路(上),无源滤波器2022-01-11 1977
-
无源带通滤波器的仿真实例电路原理图免费下载2021-03-30 1915
-
无源RC滤波器设计性的实验方案构思资料说明2019-07-09 1903
-
RC无源低通滤波器设计问题?2019-01-08 4034
-
带通滤波器电路图大全(三款带通滤波器电路设计原理图详解)2018-03-26 324589
-
RC无源滤波器电路2018-02-26 19678
-
0.5Hz~3.5Hz的无源RC带通滤波器电路以及参数选择2016-05-14 4534
-
无源RC滤波器设计性学生实验方案构思2016-01-14 1104
-
RC无源滤波电路及其原理2011-11-10 50656
-
双象限RC带通滤波器2009-09-17 970
-
无源低通滤波器电路,有源低通滤波器原理图2008-09-24 23331
全部0条评论

快来发表一下你的评论吧 !

