

MEMS惯性传感器的惯性导航位姿解算基础框架
电子说
描述
根据自己对惯性导航姿态解算的学习,简单总结一下自己对惯导解算认识。先画一张从传感器数据到最终位姿的过程梳理图。

01 平台式惯性导航系统和捷联惯性导航系统
平台式惯导的系统主体是平台,平台始终跟踪当地的水平面,轴向始终指向东北天方向。利用位于稳定平台上的加速度计测量载体在导航坐标系下的xyz轴的加速度,积分得到位移速度和位置。 缺点:其体积和重量大,而平台也是一个高精度、复杂结构的机电控制系统。
捷联式惯性导航系统 (Strapdown inertial navigation system) Strapdown 具有“捆绑”的意思, 陀螺仪、加速度计与载体“捆绑”。载体的姿态和航向可以用载体坐标系(b系)相对于导航坐标系(n系)的三个转动角决定。就是说,在捷联式惯性导航系统中,直接测得的三个方向的加速度是载体坐标系三个轴方向上的,需要用一个捷联矩阵C将其变换到导航坐标系中来。
02 坐标系
运载体中三维空间运动包含六个自由度,既有角运动也有线运动。在地球表面附近,运载体的角运动描述一般以当地水平面和地理北向为参考基准;线运动的描述通常采用地理经度、纬度和高度表示,它是相对于整个地球旋转椭球体而言。
但是,运载体上惯导系统使用的关系传感器(陀螺仪和加速度计)从原理上看是相对于惯性空间进行测量的。另外,地球绕其自转轴相对于惯性空间以常值角速率旋转,运载体在地球表面位置变化会引起其相对于地心的角速率。
03
惯性传感器
以 MEMS 惯性传感器为例,通过“感触”地球引力场和自旋角速度(加速度计和陀螺仪)通过数学算法(积分)获得角速度、加速度、速度、位置等基础参数。 因为传感器测量的误差存在,在积分运算时,势必将测量误差引入了积分,随着时间的累积,积分误差也一直在累加。因此在整个姿态解算前,对误差建模分析与补偿尤为重要。
误差来源
对MEMS 惯性传感器来说,引起误差的主要原因有: 1) 惯性器件本身结构的不完善和工艺差异 2) 惯性器件内部物理因素变化如温度、杂散磁场等 3) 外界环境如温度变化、外界磁场干扰、载体剧烈变化等
误差模型
根据不同的(确定性和随机)误差参数分析,推导出误差模型(数学公式)。
对确定性误差参数是可辨识的(这种辨识是指通过一定的标定方法可以补偿,基本消除的误差)。常用六面法借助于转台标定加速度和陀螺仪。
不需要转台的标定常用 迭代优化方法。`参考文献:D. Tedaldi, A. Pretto and E. Menegatti, “A Robust and Easy to Implement Method for IMU Calibration without External Equipments”. In: Proceedings of the IEEE International Conference on Robotics andAutomation (ICRA 2014), May 31 - June 7, 2014 Hong Kong, China, Page(s): 3042 - 3049`
对随机误差常用 Allan方差分析
04 传感器输出的原始单位数据 直接输出角度 3轴加速度计寄存器读取到的十六进数据 和 选择的测量范围决定加速度数据的测量精度。Eg:加速度计读到的数字是1000,那么对应的加速度数据是1000/2048=0.49g 因此,利用加速度计测量重力向量在感应轴上的映射。被测加速度的振幅随感应轴与水平面的夹角α的正弦值的变化而变化,可以推算出三轴的倾斜角度。



利用三角函数计算俯仰和滚转角

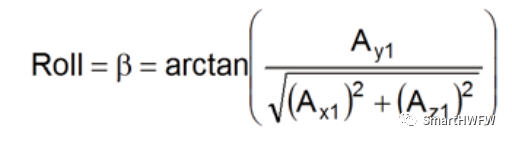
特别要注意:加速度计绕 Z 轴旋转时,各轴的重力分量不会变化。因此,不用推算 yaw 角解算。一般采用磁力计推算。
3轴陀螺仪从寄存器读取到的十六进数据 和 选择的测量范围决定陀螺数据的测量精度。Eg:当读取陀螺仪的值是1000,对应的角速度计算如下:32767/2000 =1000/x; 即 x = 1000/16.4(°/s) 因此,利用陀螺仪直接输出角度时,将需要把角度 °/s 换算成弧度。即:1°/s = π/180 = 57.3rad/s。对3个轴转动的角速度积分,可以得到角度。
数据融合
通过上述方法直接利用加速度计和陀螺仪是可以输出角度的。但是往往在具体的应用中加速度计和陀螺仪都表现出不同的特性。
由于加速度易受高频噪声干扰,因此算得的姿态角是很不稳定的,不能直接参与控制。陀螺仪对振动不敏感,不产生高频噪声,但陀螺仪有零偏、积分出的姿态会飘移。在应用中加速度计对高频振动噪声比较敏感,陀螺仪对低频噪声敏感。
| 对比项 | 加速度计 | 陀螺仪 |
| 高频振动噪声 | 敏感 | 无感 |
| 低频姿态飘移 | 不飘 | 会飘 |
如上对比,因为加速度和陀螺仪都存在各自的不足之处,因此我们需要引入数据融合(滤波算法)。 常见的滤波算法:DMP直接输出角度 > 卡尔曼滤波 > 四元数解算 > 清华角度滤波 > 一阶互补滤波 在项目中常用:EKF、DCM/Mahoney、Madgwick(基于梯度下降法)等算法
`参考文献:Madgwick S O H, Harrison A J L, Vaidyanathan R. Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//Rehabilitation Robotics (ICORR), 2011 IEEE International Conference on. IEEE, 2011: 1-7.`
位姿表达
在 AHRS 系统下描述的是载体坐标系的轴系相对于导航坐标系的轴系之间的角度关系(方向)。通常用欧拉角法或者四元数法表达。常用的方法还有:方向余弦矩阵法、等效旋转矢量法。 在采用欧拉角时需要考虑的问题是:万向节死锁 不同的旋转规则下死锁的情况不一样,在Z Y X 的顺规下,当pitch角度为90或-90的时候,roll和yaw角度会乱飘,这就是遇到了万向节的死锁。
因此,很多做方案的公司都是用四元数表征传感器的姿态。在这个地方 yaw 角是通过地磁传感器解算的。地磁传感器测量的是自身和磁北的角度。北东地坐标系和磁北不是同一个方向。 单位四元数(Unit quaternion)可以用于表示三维空间里的旋转。四元数表示能够更方便地给出旋转的转轴与旋转角。
// 绕Y轴旋 eulerAngle.pitch = asinf(2 * q0 * q2 - 2 * q1 * q3) * (180 / PI); // 绕X轴旋转 eulerAngle.roll = atan2f(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2 * q2 + 1) * (180 / PI); // 绕Z轴旋转 eulerAngle.yaw = atan2f(2 * q1 * q2 + 2 * q0 * q3, -2 * q2 * q2 - 2 * q3 * q3 + 1) * (180 / PI);
05
通过一次二次积分获得速度和位置
在载体坐标系下通过矩阵转换到导航坐标系后,加速度计包含的重力加速和运动加速度。积分是只针对运动加速度积分。所以,需要把重力加速度给补偿掉。
然后一次积分得到速度,二次积分得到位置。但是积分存在累加误差,因此在室外的时候通过 GNSS 对速度和位置做修正。
是呢环保局:郭婷
-
MEMS惯性传感器都有哪些种类?MEMS惯性传感器有哪些特点2025-08-26 791
-
MEMS惯性传感器的研究背景与发展现状2023-07-19 3763
-
惯性传感器2021-09-01 1507
-
MEMS惯性传感器选型表2021-05-26 1316
-
3dm-gx5-25_微惯性航姿系统2020-12-09 1311
-
MEMS惯性传感器的趋势分析2020-08-28 3658
-
惯性导航模块特征和 优势有哪些?2020-08-13 2296
-
基于单晶硅传感器的MEMS惯性传感器工作方式2020-07-07 3232
-
MEMS惯性传感器的测试及应用领域2020-05-18 6060
-
MEMS惯性传感器的优势是什么?2019-11-05 3603
-
MEMS惯性传感器与工业环境2019-09-03 2222
-
装配MEMS惯性传感器的实用方法2018-11-12 1897
-
MEMS惯性传感器轻松解决应急救援定位问题2018-10-30 3129
-
MEMS惯性传感器的背景及发展现状2018-02-23 9581
全部0条评论

快来发表一下你的评论吧 !

