神经网络面临的问题和挑战

1、多层神经网络复杂化，提升效率成为新挑战

神经网络从感知机发展到多层前馈神经网络，网络变得越来越复杂。如上一篇 机器学习中的函数（2）- 多层前馈网络巧解“异或”问题，损失函数上场优化网络性能 讨论针对前馈神经网络我们的目标是要让损失函数达到最小值，这样实际输出和预期输出的差值最小，利用最小化损失函数提升分类的精度。显然，采用“穷举”找优参数的方法不是聪明的选择，费时费力。我们现在面临的问题和挑战变成，如何找到一个高效的方法从众多网络参数（神经元之间的连接权值和偏置）中选择最佳的参数？这就是我们即将一起学习讨论的话题。

在研究复杂问题之前，我们先要弄清楚几个基础概念，包括“凸函数”，“梯度”，“梯度下降”。

2、基础概念：凸函数和凸曲面、梯度和梯度下降

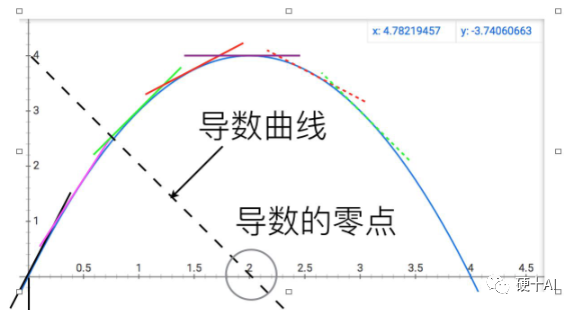
讨论这些概念前必须向伟大的牛顿致敬，当科学发展到伽利略和开普勒那个年代，人们就在物理学和天文学中遇到很多求一个函数的最大值或最小值，即最优化问题，比如计算行星运动的近日点和远日点距离等。如何系统地解决最优化问题？牛顿创造性的给出了答案，他的伟大之处在于，他不像前人那样，将最优化问题看成是若干数量比较大小的问题，而看成是研究函数动态变化趋势的问题 。如下图，牛顿对比抛物线和它的导数（虚的直线），发现曲线达到最高点的位置，就是切线变成水平的位置，或者说导数变为0的位置呢。他把比较数大小的问题，变成了寻找函数变化拐点的问题，同时发明导数这种工具将这两个问题等同起来，利用导数这个工具求最大值问题就变成了解方程的问题，你看微积分这种强大的数学工具在神经网络中多重要啊。

（1）凸函数和凸曲面

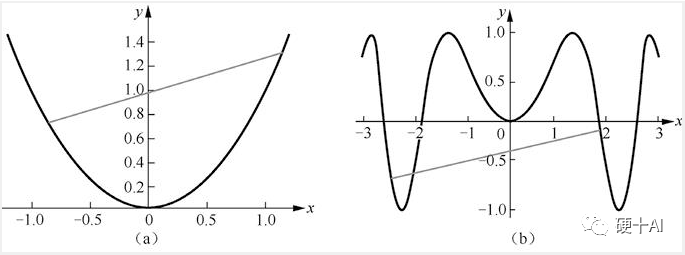
凸函数的直观认识：下图中上述［图a］是凸函数图像，［图b］是非凸函数图像，“任意两点连接而成的线段与函数没有交点”即为凸函数。

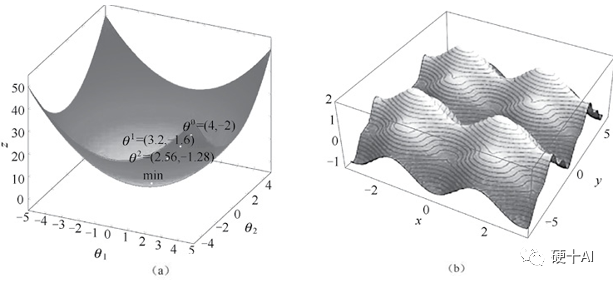
从凸曲面与非凸曲面理解最小值和局部最小值：凸函数的局部极小值就是全局最小值，如下图中【图a】凸曲面中无论弹珠起始位置在何处，弹珠最终都会落在曲面的最低点，而这个极小值恰好是全局最小值。而非凸函数求导获得的极小值不能保证是全局最小值，如【图b】非凸曲面中弹珠仍然会落在曲面的某个低点，但有可能不是全局的最低点。

（2）梯度和梯度下降法

梯度（gradient）的本质是一个向量（有大小和方向两个要素），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着此梯度的方向变化最快，变化率最大。为求得这个梯度值会用到“偏导”的概念，“偏导”的英文是“partial derivatives”，若译成“局部导数”更易理解，对于多维变量函数而言，当求某个变量的导数时，就是把其他变量视为常量，然后对整个函数求其导数，由于这里只求一个变量，即为“局部”。接着把这个对“一个变量”求导的过程对余下的其他变量都求一遍导数，再放到向量场中，就得到了这个函数的梯度。

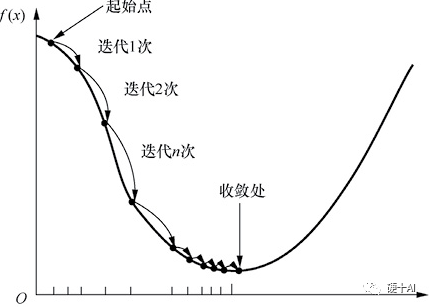
梯度下降法（Gradient descent）是最常见的一种最优化问题求解方法。打个比方，假设一个高度近视的人在山的某个位置上（定义为起始点），他计划从从山上走下来，也就是走到山的最低点。这个时候，他可以以起始点为基准，寻找这个位置点附近最陡峭的地方，然后朝着山的高度下降的方向走，如此循环迭代，最后就可以到达山谷位置。梯度下降过程示意如下图所示，当我们沿着负梯度方向进行迭代的时候“每次走多大的距离”是需要算法工程师去调试的，即算法工程师就是要调试合适的“学习率”，从而找到“最佳”参数。如果碰到极大值问题，则可以将目标函数加上负号，从而将其转换成极小值问题来求解。

3、BP算法提升效率，让人工智能再次进

如本文开头提到的，上世纪70年代多层神经网络出现后，面临重大的挑战是增加神经网络的层数虽然可为其提供更大的灵活性，让网络能解决更多的问题，但随之而来的数量庞大的网络参数的训练，这是制约多层神经网络发展的一个重要瓶颈。这时误差逆传播（error BackPropagation， 简称BP）算法出现了。现在提及BP算法时，常常把保罗·沃伯斯（PaulWerbos）称作BP算法的提出者，杰弗里•辛顿（Geoffrey Hinton）称作BP算法的推动者。

1974年，沃伯斯（图a）在哈佛大学取得博士学位，在他的博士论文里首次提出了通过误差的反向传播来训练人工神经网络，沃伯斯的研究工作，为多层神经网络的学习、训练与实现，提供了一种切实可行的解决途径。

1986年，辛顿教授（图b）和他的团队优化了BP算法，吻醒了沉睡多年的“人工智能”公主，让人工智能研究再次进入繁荣期。

BP算法其实并不仅仅是一个反向算法，而是一个双向算法，它其实是分两步走①正向传播信号，输出分类信息；②反向传播误差，调整网络权值 。

BP 算法基于梯度下降（gradient descent）策略，以目标的负梯度方向对参数进行调整，采用“链式法则”（链式法则用于求解复合函数的导数，复合函数导数是构成复合的函数在相应点的乘积，就像锁链一环扣一环，所以称为链式法则）。

BP算法的工作流程拆解开如下，对于每个训练样例BP算法执行的顺序是

先将输入示例提供给输入层神经元，然后逐层将信号前传，直到产生输出层的结果。

然后计算输出层的误差，再将误差逆向传播至隐层神经元。

最后根据隐层神经元的误差来对连接权和阈值进行调整。

该迭代过程循环进行，直到达到某些停止条件为止，例如训练误差已达到一个很小的值。实际应用中BP算法把网络权值纠错的运算量，从原来的与神经元数目的平方成正比，下降到只和神经元数目本身成正比，效率和可行性大大提升，而这个得益于这个反向模式微分方法节省的计算冗余。

4、BP算法的缺陷

BP算法在很多场合都很适用，集“BP算法”之大成者当属Yann LeCun（杨立昆），纽约大学教授2018年还拿过图灵奖，担任过Facebook首席人工智能科学家。1989年，LeCun就用BP算法在手写邮政编码识别上有着非常成功的应用，训练好的系统，手写数字错误率只有5%。LeCun借此还申请了专利，开了公司，发了笔小财。但如前所述，BP算法的缺点也很明显，在神经网络的层数增多时，很容易陷入局部最优解，亦容易过拟合。20世纪90年代，VladimirVapnik（万普尼克）提出了著名的支持向量机（Support Vector Machine，SVM），虽然SVM是一个特殊的两层神经网络，但因该算法性能卓越，具有可解释性，且没有局部最优的问题，在图像和语音识别等领域获得了广泛而成功的应用。在手写邮政编码的识别问题上，LeCun利用BP算法把错误率降到5%左右，而SVM在1998年就把错误率降低至0.8%，这远超越同期的传统神经网络算法。这使得很多神经网络的研究者转向SVM的研究，从而导致多层前馈神经网络的研究逐渐受到冷落，在某种程度上万普尼克又把神经网络研究送到了一个新的低潮期。

神经网络又是如何度过这个低谷期，快速进入到下一个繁荣时代的呢？　　

      审核编辑：彭静