

哪些网格才能成为Fluent眼中的”好孩子“呢?
电子说
描述
我们使用各种工具进行Fluent仿真的前处理工作,目的是获得适合于流体计算的有限元网格。
对于不同的网格,他们的数量、类型、分布、形状……等特点都不尽相同,但是对于绝大多数的体网格来说,都还是能够在Fluent中进行仿真计算的。
这个时候,Fluent就好像一个成熟稳重的“成年人“,而这些形形色色的网格则好比一群”孩子“一样。Fluent需要接纳这些”孩子“并进行计算,但是也会对孩子的情况进行反馈和评判。本文就简单的探讨一下,哪些网格才能成为Fluent眼中的”好孩子“呢?
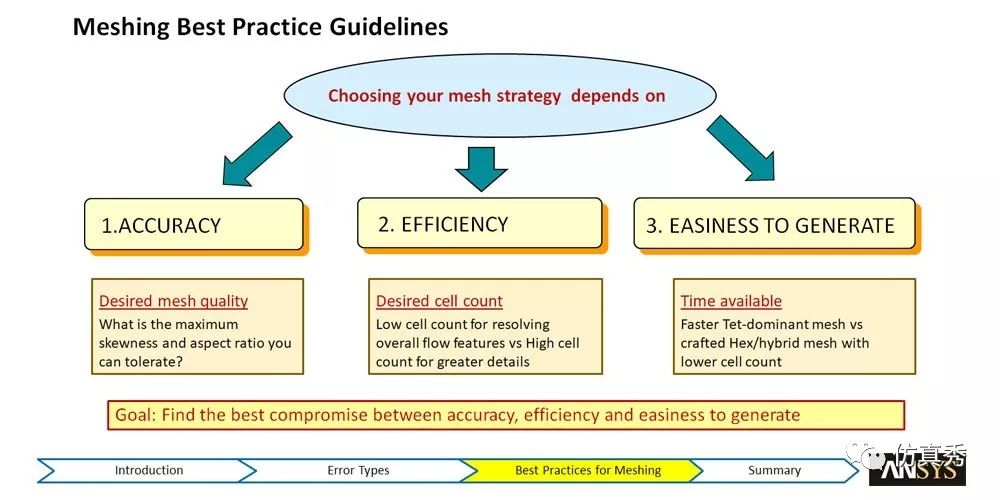
图1 ANSYS官方教材中优质网格应具备的条件
在流体仿真的工业应用中,网格的要求主要包括以下三个方面:准确、高效、易于生成。但需要注意的是,Fluent软件本身对网格的要求并没有那么高。
比如在17.0版本之后,对于高扭曲度的网格,Fuent还提供了一种包裹的方法进行修正,以避免非物理解的存在。从这个角度来讲,Fluent可以认为是一个很宽容上进的“成年人”,不断的在改进自身的能力和素质,以适应不同类型“孩子们“的需求,而且持续的在降低进屋的门槛。

图2 高扭曲度网格的包裹修正,实际上是降低了对网格的要求
就像我们都喜欢有教养、懂礼貌、活泼、可爱的孩子一样,Fluent对于网格的偏好也是有明确的量化指标的。但是对于一个网格来讲,他的特点是包含很多方面的,究竟哪些特性是能够吸引Fluent,或者说哪些是主要被Fluent这个成年人所关注的呢?
是六面体么,还是Cutcell或Polyhedral?是通过Gambit生成的网格、还是表面图案整齐一致的网格呢?
★ 名词的释义
网格的好坏(优劣),一般情况下都被大家等同于网格质量,这个概念从广义上理解是没有错的。毕竟质量好,就证明是优秀的;质量差,也就可以认为是劣质的。
但需要注意的是,我们有限元仿真的网格中有一个专有名词,就叫做“网格质量”(Mesh Quality)这是一个定量的描述,就好像和“网格数量“的概念是一样的。“网格质量”虽然有多种衡量方式,但是每一种标准都是一个数值;可大、可小,可以定量计算,也可以统计分布。
因此,为了避免概念上的混淆,在本文中,我们就用“网格扭曲度”这个词来代表“网格质量”的专有概念。同时,也会尽量的避免出现“质量”这两个字。
但是网格的特征实在是太多了,比如他的数量、类型、分布、形状等等因此我们可能需要借助一些方法来看这个问题。唯物辩证法中关于事物的特点,有一个重要的概念叫“重点论”:简单的理解就是在不同的情境下,应该抓住事物的主要矛盾。
流体仿真需要的网格有很多的特点,从辩证法的角度,我们可以认为这些特点都是一个一个的矛盾。那么既然要抓住主要矛盾,就必须要知道哪些因素是优先考虑的。
对于Fluent仿真来讲,主要矛盾只有两个:一是网格的效率与准确性;二是网格的扭曲度。

图4 ANSYS官方培训教材中,也将“效率与准确性”和“扭曲度”列为网格最重要的特征
因此,只要能够满足这两条“矛盾“的网格,Fluent认为都是好的网格;至于其他的因素,比如网格的类型、是否包含Interface交界面、生成网格使用的软件、网格是否整齐、外观是否好看等,都是次要矛盾。这些次要矛盾并不会影响Fluent对该网格的”看法“,简单的讲,就是不会对仿真结果有过多的影响。
但是网格的效率、准确性和扭曲度,却会对Fluent仿真的求解造成决定性的影响。
★ 网格的效率与准确性
首先我们来分解这个概念。
● 效率:就是网格的数量不能太多,因为这样会导致总体的仿真时间过长,从而降低效率。
● 准确性:就是计算的结果要合理,各个位置变量的值(和梯度)要能够准确的体现出来。
因此,如果我们希望网格满足效率与准确性的要求,就必须要做到:该密的地方密,其他的地方稀疏。哪些地方的网格该密呢?主要有两个区域:
※ 几何具备精细细节的位置
几何细节的精细程度通常是在以下两种情形中体现出来的:一是有弧(曲面)的地方;另一个则是有狭缝的地方。如果我们不加密曲率大的几何区域,那么曲面将变形失真;如果狭缝的区域不进行加密,则会出现网格的尖角。
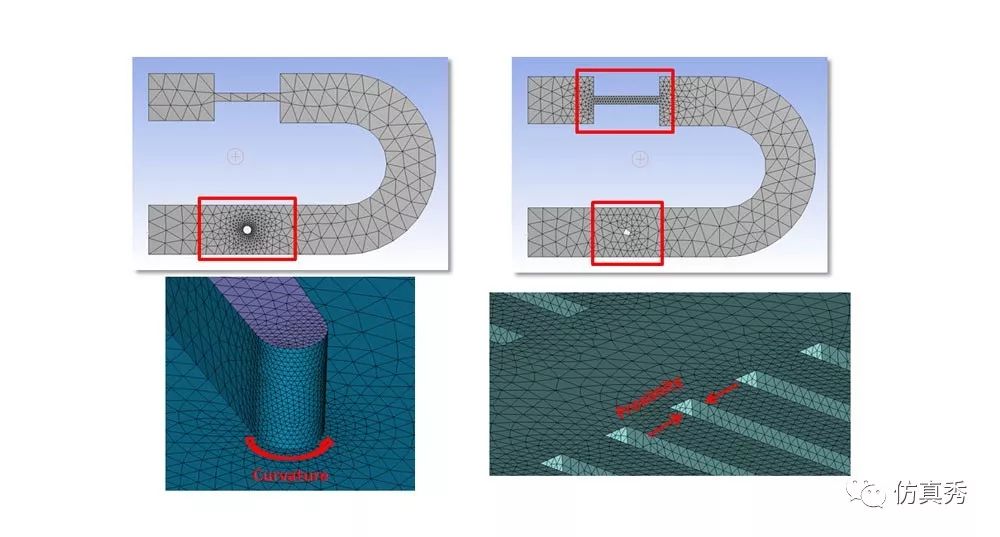
图5 曲率和狭缝使几何细节加密中最为常见的特征
※ 变量存在大梯度的位置
很显然,如果一个变量在较小的区域发生了较大的改变,那么如果网格数量不够的话,则是不能准确描述这种梯度变化的。毕竟我们的仿真采用的是离散的方法,一个网格只能代表一个值,所以当梯度大的时候,必须要用多个网格才能准确描述。
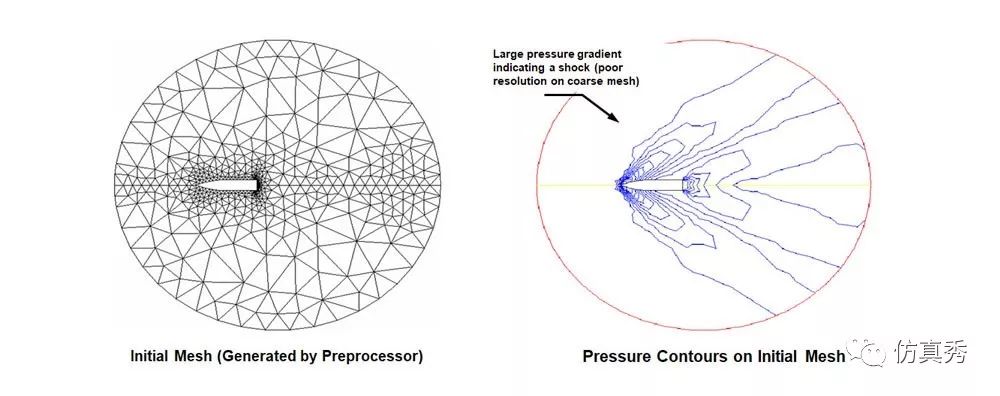
图6 当网格不能捕捉大梯度变量时,计算结果往往是不正确的
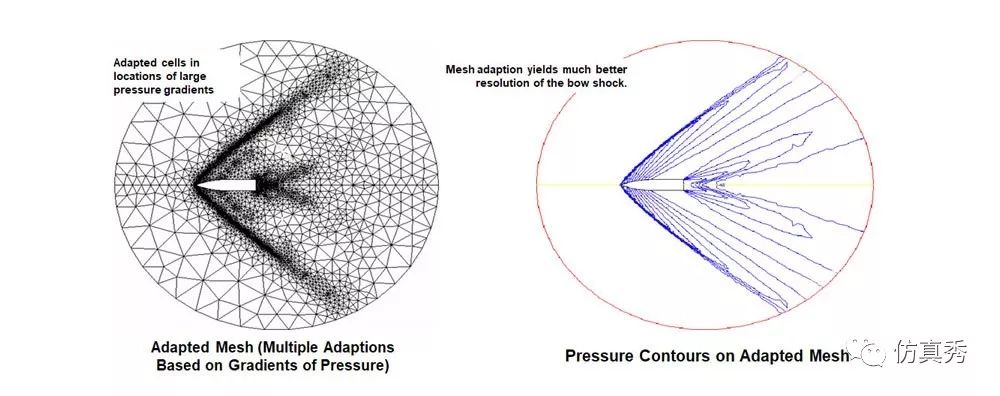
图7 当网格能够捕捉大梯度变量时,计算结果才能得到保证
通常,如果我们不首先进行仿真计算的话,是很难确定哪些区域存在大梯度变量的。当然,对于成熟的流体工程师,经验可能会给我们以指导。为此,我们需要在网格划分之前就能够粗略的判断,可能出现的大梯度变量的位置。对于这些位置,我们可以通过影响体的方法进行局部的网格加密。
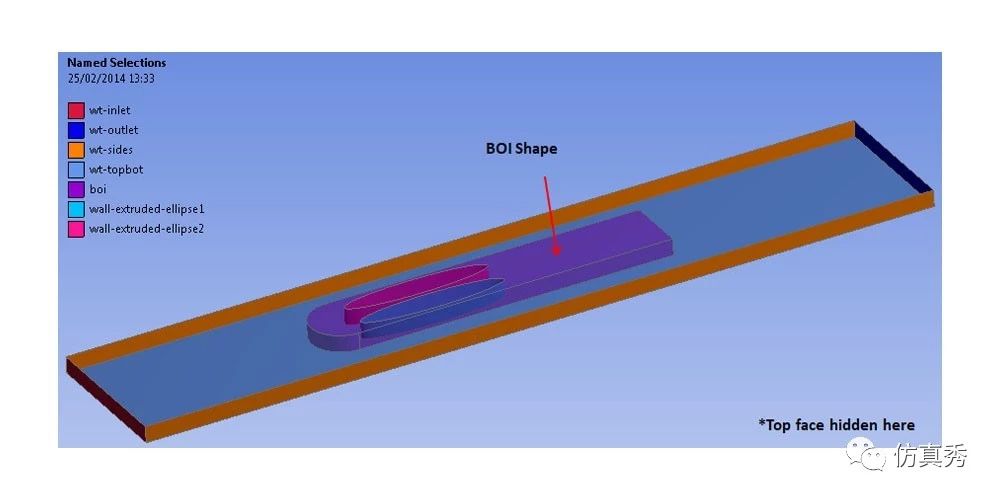
图8 经验告诉我们,应该在障碍物的下游方向加密网格
对于其他的、无法预判的大梯度变量区域,我们只能依赖Fluent中的网格自适应功能,在求解之后进行局部加密,当然,这个也是已经非常成熟的方法了。
除了影响体(或球)的方法局部加密以外,边界层网格也是一个自动加密大梯度变量的有效途径。所以,Fluent会非常喜欢有边界层的网格,因为他们即准确又高效。
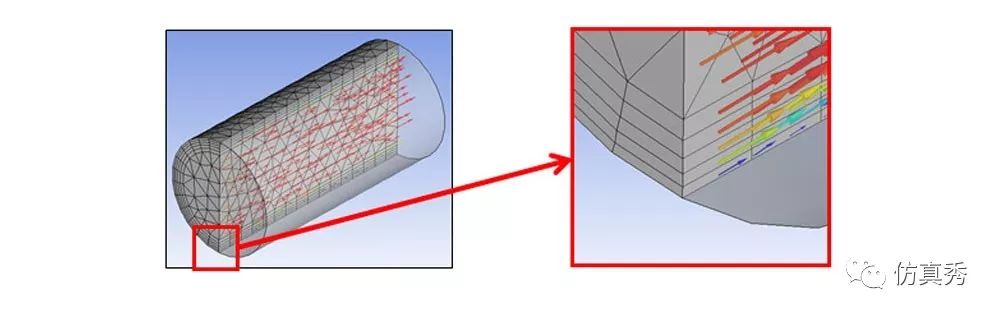
图9 Fluent最喜欢有边界层的网格
如果所有的位置网格都很稀疏,那么将无法有效捕捉变量的大梯度、也无法准确描述几何的实际特征,计算可能会出现大的错误;如果所有位置的网格都很密,那么计算量会过大,而且在梯度小的区域,过多的网格没有任何的意义,这不满足效率优先的要求,实际上也造成了资源的浪费。
★ 网格的扭曲度
对于自动生成的体网格(非六面体),网格的扭曲度基本上就可以定量的衡量“网格的质量“这一专有概念了,因为skewness和长宽比、过渡等属性评判的标准都是类似与统一的。对于六面体而言,网格的扭曲度恐怕不能完全的覆盖所有的评判标准,还需要长宽比、网格间过渡等指标进行联合判别。
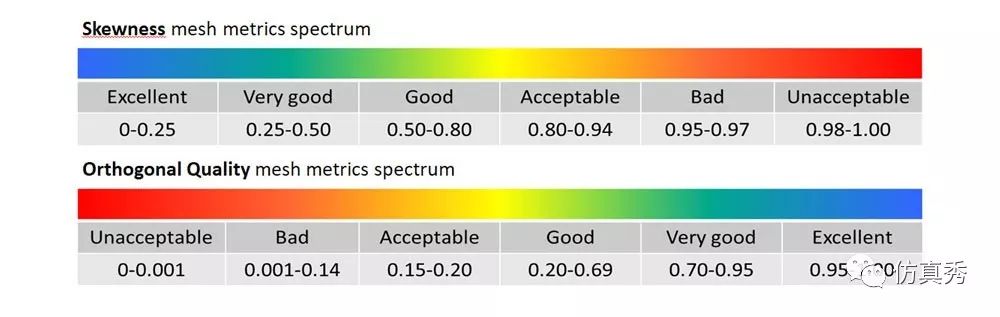
图10 网格扭曲度的判别标准
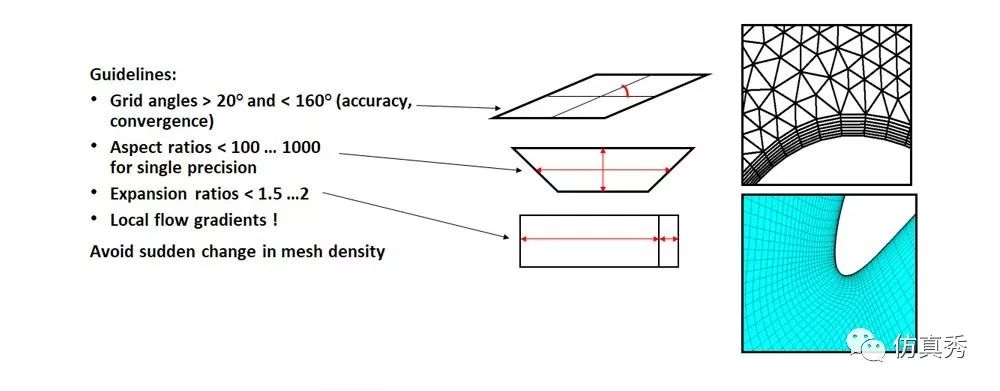
图11 六面体网格的额外判别标准
以上两个概念(效率与准确性、扭曲度)都是Fluent眼中优质网格必备的特点,但是他们两个的定位还有所区别。
效率与准确性可以认为是决定性的因素,他是所有网格必须优先考虑、并依照该要求进行布局和生成的标准。相反,网格的扭曲度可以认为是一个“一票否决权”;他平时并不出现,也不干涉网格构建的流程,只是在网格完工之后出现,更像是一个监管的部门;它的工作就好比工程中的验收一样,没有问题最好;如果有问题了,就必须要处理一下。
根据我们的调查显示,绝大部分的工程师在构建流体网格的时候,通常是忽略了效率与准确性的要求,而仅仅是判断一下网格扭曲度就做结论了,这是不合理的,也是不负责任的。举一个例子,假如一个流体网格不能够在大梯度变量存在的区域有足够多的网格,那么就会出现我们非常常见的流体仿真问题:残差不收敛、粘性比超标、计算发散……
最后总结一下,在Fluent这个宽容的“成年人“眼里,好孩子(网格)的标准只有这些:有礼貌(效率)、有教养(准确性)、活泼可爱(扭曲度)。
因此,喜欢一个孩子(网格),不会在乎他是男孩(六面体)还是女孩(四面体)、也不会在乎他是高还是矮(是否包含Interface交界面),是什么出身背景(用哪种软件生成的)、相貌如何(网格是否整齐)、性格外向(cutcell网格)还是内敛(Poly网格)。
好了,哪些网格才能成为Fluent眼中的”好孩子“呢?文章写完了,大家自行判断!当然网格划分只是软件操作其中重要的一步,但是只会软件操作是不够的。
对于想要从事流体仿真工程师岗位的高校学生和转行工程师来说,仅仅是掌握了软件的操作方法,并不等于会做仿真。
仿真是一整套体系,仿真工程师的成长也是一整套体系。
审核编辑 :李倩
-
人生哪个阶段的梦想最有可能成为我们最后的梦想呢?2012-12-01 3161
-
为什么说软件无线电能成为开放无线电?2019-08-02 2087
-
具备哪些知识才能成为真正的嵌入式工程师???2020-07-13 1784
-
如何才能成为一名嵌入式大牛呢?2021-01-18 1676
-
完全自动驾驶车辆何时才能成为现实?2021-02-04 1908
-
软件无线电如何才能成为开放无线电?2021-05-24 2012
-
云计算为什么能成为物联网的秘密武器?2021-06-18 2240
-
如何才能成为一名单片机高手?2021-07-01 1869
-
STC89C52_51单片机_例程5_长短按键_定时***_要怎样努力才能成为很厉害的人? 精选资料分享2021-07-20 1007
-
如何才能成为一个数字验证工程师?2021-09-18 1587
-
如何才能成为嵌入式Linux开发工程师2021-11-04 1223
-
如何才能成为一个硬件工程师?2021-11-11 1937
-
如何才能成为一名单片机工程师?2021-12-23 4030
-
工程师故事:怎样才能成为优秀研发工程师呢?2012-03-22 4359
-
如何才能成为高级嵌入式开发工程师2019-08-29 5440
全部0条评论

快来发表一下你的评论吧 !

