

Wolfram语言与Mathematica13.1版本上线
描述
大学微积分
大学微积分转化是Mathematica最初的成就之一。但直到现在,我们仍在继续增加新功能,将微积分变得更加简单,也能更快地连接到其他应用。我们一直有D函数,可以在某处求导。在13.1版本,我们增加了ImplicitD,可以进行隐函数求导。
例如,它可以求xy关于x的导数,其中y由约束条件x2 + y2 =1的隐式决定:
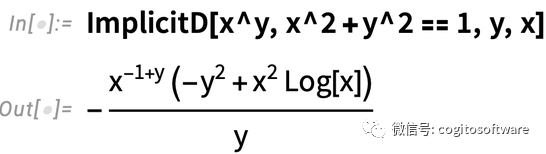
省略第一个参数,会得到标准大学微积分“求曲线切线的斜率”:
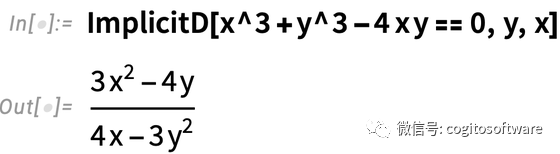
到目前为止,以上所有都是对长期存在的微积分功能简单直接的重新整理。确实,这些隐函数求导功能在Wolfram|Alpha中已经存在很长时间了。但是对于Mathematica和Wolfram语言来说,我们希望每个功能都能尽可能普遍,也是为支持出现在微分几何中的内容以及微分方程隐式解的渐进和验证。除了常规的大学微积分之外,ImplicitD也可以做其他事情,比如,在由两个曲面的焦点定义的曲线上,求二阶隐式的导数:
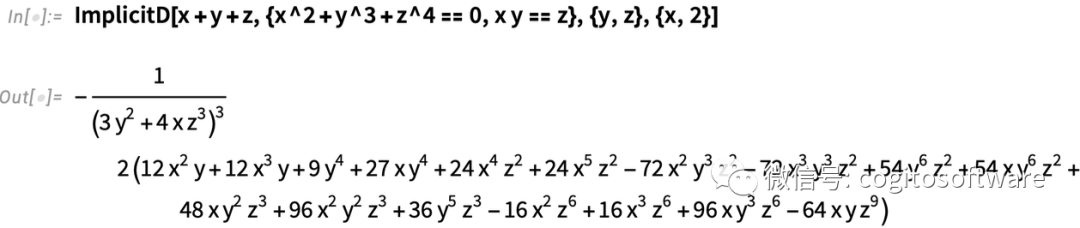
在Mathematica和Wolfram语言中,Integrate函数可以给你答案。(在Wolfram|Alpha中也可以得到分步计算过程。)但出于课程目的——或有时突破可能界限时——分步求解积分是非常有用的。所以在13.1版本中,我们添加了IntegrateChangeVariables函数,用于改变积分中的变量。有个直接的问题:如果用Integrate[...]函数指定积分,Integrate会继续进程计算该积分:
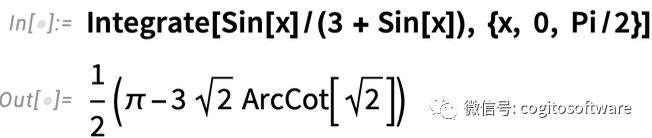
但是如果要用IntegrateChangeVariables,则需要一个“未完成”的积分。可以通过使用Inactive达到这一目的,例如:
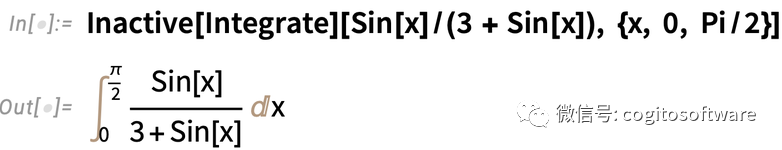
基于这一未转换形式,可以使用IntegrateChangeVariables进行“三角代换”:
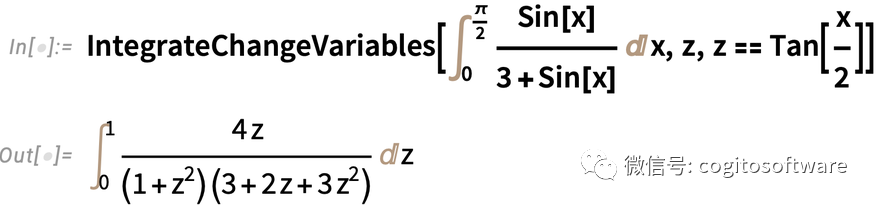
结果又是未转换的形式,但以不同的方式阐述积分。Active继续进行,并计算积分:
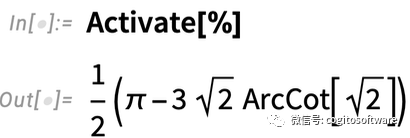
IntegrateChangeVariables可以处理多重积分——但要与命名的坐标系相结合。以下是将双重积分转换为极坐标:
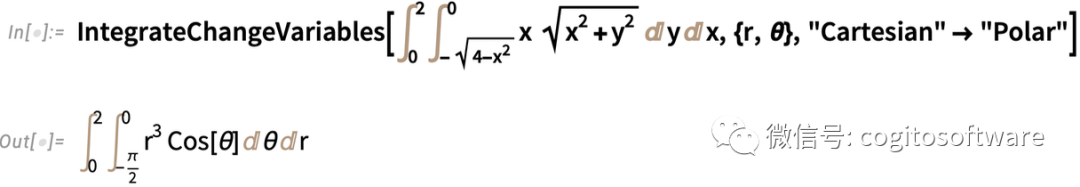
尽管积分变量的基本“结构”转换非常直接,但IntegrateChangeVariables相关的内容还是非常复杂的。大学微积分变量的改变常常经过精心编排,从而更容易算出来。在常规情况下,IntegrateChangeVariables最终要对几何区域进行重要转换,在某些约束条件下难以简化被积函数等等。
除了在积分中改变变量,13.1版本还引进了DSolveChangeVariables,用于改变微分方程中的变量。以下是将拉普拉斯方程转化为极坐标的过程:
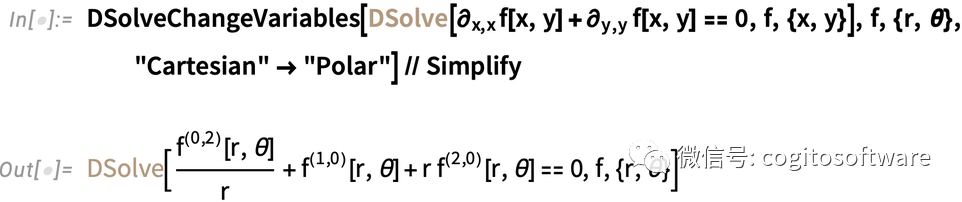
有时改变变量非常简便。但有时(比如广义相对论)可能导出完全不同的系统视图。比如,以下是指数变换将普通的柯西-欧拉方程转换为有常数系数的形式:
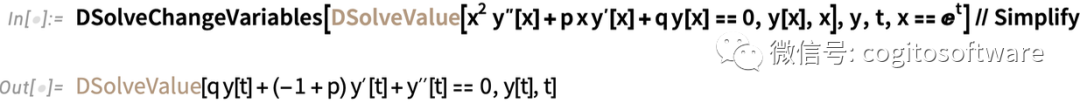
分数阶微分
x2的一阶导数是2x;二阶导数是2。那么二分之一阶导数是多少?即使在微积分出现的最初几年,这一问题也经常被问到(例如莱布尼茨)。到19世纪,黎曼和刘维尔给出了答案,在13.1版本中,也可以用新函数FractionalD来计算:

计算另一个二分之一阶导数,会回到一阶导数:

在更普遍的情况下,有:
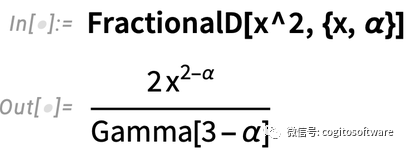
对于负阶导数也可用,所以,例如,-1阶导数是它的不定积分:

计算分数阶导数与计算分数阶微分一样困难。但是FractionalD依然可以做到

即使结果可能会变得非常复杂:
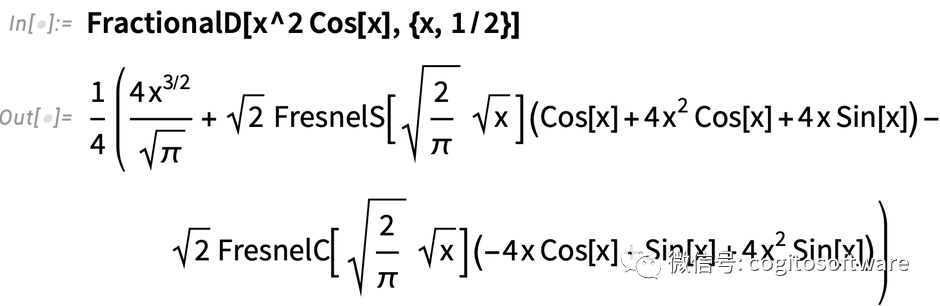
为什么FractionalD是一个单独的函数,而不是D函数的衍生部分?我们讨论过很多次这个问题。我们引入明确的函数FractionalD是因为分数阶导数没有一个明确的定义。事实上,在13.1版本中,我们也支持卡普托分数阶导数(或差分积分)CaputoD。
对于x2的二分之一阶导数,答案还是一样:
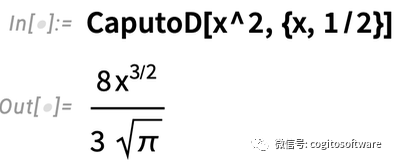
但只要函数在x =0处不为0,答案可能会有所不同:
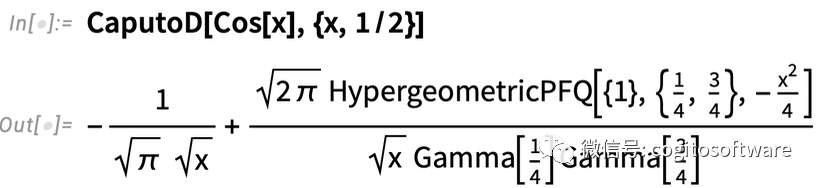
在处理拉普拉斯变换和微分方程时,CaputoD是分数阶微分非常方便的方法。在13.1版本中,我们可以计算CaputoD,也能进行积分变换并求解涉及它的方程。
以下是二分之一阶微分方程
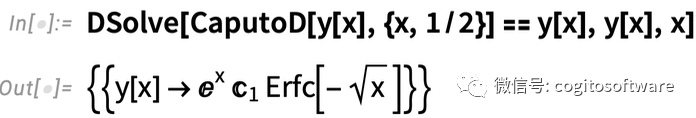
以下是二分之三阶微分方程
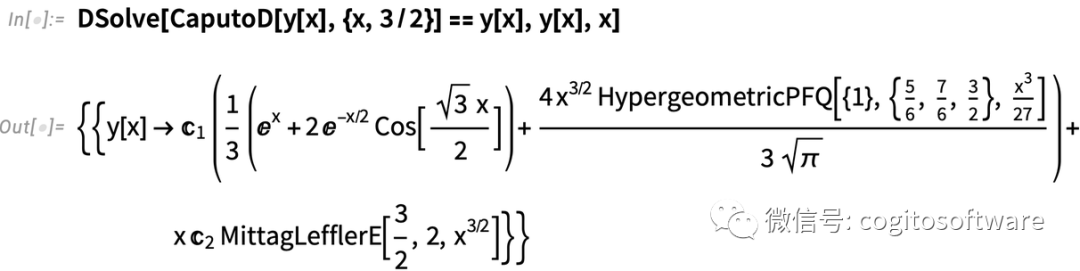
以及π阶微分方程:
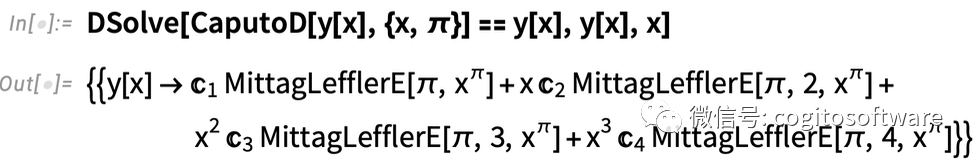
注意MittagLefflerE。这一函数(出现于9.0版本)对于分数阶导数起的作用与Exp对于普通导数的作用一样。
审核编辑:汤梓红
- 相关推荐
- 热点推荐
- Wolfram
- 微积分
- Mathematica
-
新版破解 Quartus II 13.1正式版(Windows版和Linux版破解)2014-01-30 177131
-
在树莓派上用Wolfram语言拍照2016-01-26 5586
-
Mathematica入门教程之Mathematica的基本语法特征2011-02-18 14482
-
Mathematica是什么?Mathematica怎样使用?Mathematica教程免费下载2018-09-13 1345
-
微信上线7.0.12版本 终于适配深色模式2020-03-23 3061
-
Wolfram语言与Mathematica13.1版本上线2022-10-21 1917
-
关于Wolfram语言与Mathematica13.1版本上线2022-10-28 1206
-
Wolfram语言与Mathematica13.1版本2022-11-11 1347
-
Wolfram语言与Mathematica 13.2版本(2)2023-02-13 1002
-
Wolfram语言与Mathematica 13.2 版本(4)2023-02-17 1341
-
Wolfram语言与Mathematica 13.2 版本(6)2023-02-21 959
-
Wolfram语言与Mathematica 13.2 版本(7)2023-02-24 936
-
Wolfram应用服务器2023-03-23 940
-
OurBMC 24.12版本正式上线2025-01-07 1377
-
NVIDIA CUDA 13.1版本的新增功能与改进2025-12-13 1831
全部0条评论

快来发表一下你的评论吧 !

