基于一般梁单元修正后的弹性地基梁单元刚度矩阵

　　在许多工程应用中，梁都是由弹性构件进行支承的，比如一些轴通常由滚珠、滚柱或轴颈轴承进行支承，一些较大的梁由弹性墙进行支承，还有一大类梁支承在地基上，一般将这类问题称为Winkler地基。

　　单排滚珠轴承可以看做是：在每个轴承处都有一个节点，并将轴承刚度加到单元刚度矩阵中对应垂直自由度的对角位置上（见图1a）：而对于滚柱或轴颈轴承，还要考虑相应的转动（力矩）刚度。 对于较宽的轴颈轴承和Winkler地基，我们使用支承介质的单位长度上的刚度s来描述（见图1b）。在支承介质所作用的长度范围内，总势能将会多出下面一项。

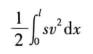　　 （1）

　　

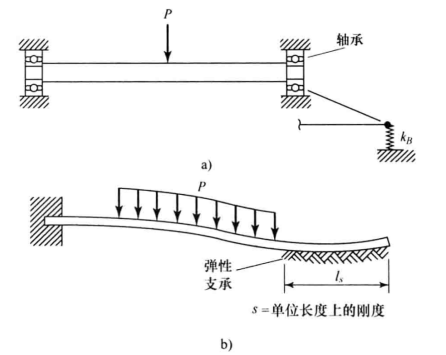
      图1 弹性支承 当我们将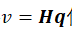代人离散化模型后，上式将变为

　　

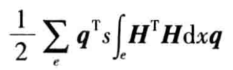
（2）

　　其中H为Hermite插值函数

　　

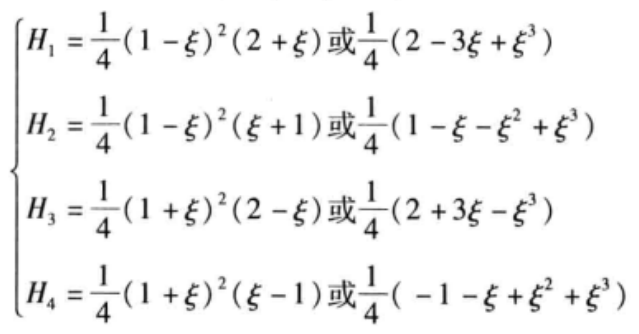
（3）

　　从公式（2）中的求和公式里，可以看出其中的单元刚度矩阵项，即

　　

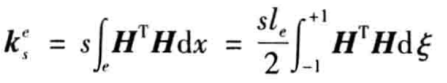
（4）

　　因为常规的梁单元刚度矩阵也是通过最小势能原理就行推导，对应的单元应变能和刚度矩阵的表达式为

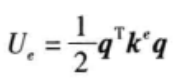　　（5）

　　

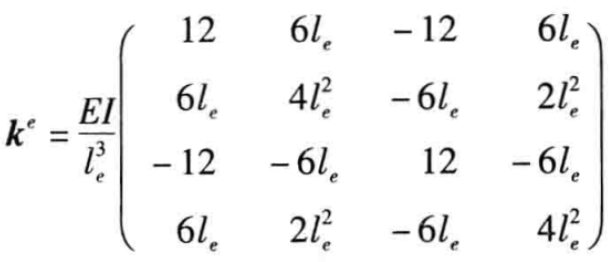
（6）

　　对公式（4）进行积分之后，可得

　　

（6）

　　对于具有弹性地基支撑的单元，这一刚度矩阵需要加入到公式（6）梁单元对应的传统的单元刚度矩阵中，即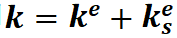。而矩阵就是弹性地基的一致刚度矩阵。 如果考虑到轴向变形，则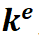为

　　

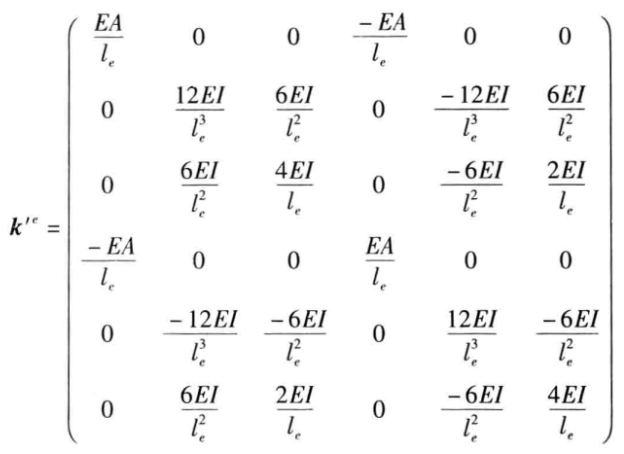
（6）

　　对应的只需要用零元素扩充轴向自由度，因为梁的弯曲和轴向变形不相互耦合。 这次课提供的弹性地基梁的有限元案例，是这种双排桩支护结构的matlab有限元编程计算分析。模型的计算简图如图2所示。

　　

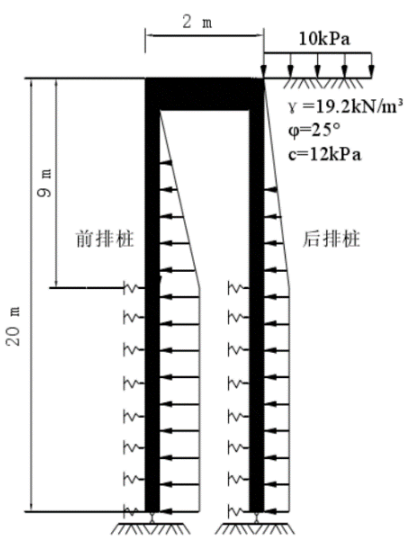
　　图2 模型计算简图 从结构上分析，双排桩支护结构如同嵌入土中的门式刚架，与单排桩的悬臂结构、多支点的混合支护结构、重力式挡土结构等支护形式的受力机理有明显的差异。开挖面下的桩体受到侧向的地基抗力在模型中简化为土弹簧反力，桩底的约束由具体的土质条件和计算模型来确定，综合考虑上述几个方面的问题后，包括桩顶结点的处理，弹性地基梁单元刚度矩阵的确定以及荷载列阵的确定等，就可以建立基本的平衡方程求解桩身各结点位移和桩身内力。 对于坑底下部的弹性地基梁单元的刚度矩阵常规方法是按集中刚度的原则先确定在单元结点处的等效弹簧刚度然后叠加到总刚。如果将上述计算的弹簧刚度按结点位置相应的叠加到总刚那么只能加到总体刚度矩阵对角线元素上。 事实上这样处理弹性地基梁单元的方法不是十分合理。上述方法只是在结点设置弹簧没有考虑到被动区土压力也是沿桩体连续分布的并不等效于各个集中弹簧力的作用并且等效刚度不是简单的将某个区域的刚度求和。为此本文提出一种思路就是考虑单元两结点间布满弹簧再将这些分布的弹簧反力转化为等效结点力建立弹性地基梁单元结点力与结点位移的关系最终可得到基于一般梁单元修正后的弹性地基梁单元刚度矩阵，如下式所示：

　　

（7）

　　刚度矩阵具体推导过程请看论文《双排桩开挖过程的改进有限元分析方法》。

　　

　　本算例用到的基本参数

　　（1）土性指标：土体粘聚力 c=12k Pa；内摩擦角 φ=25°；土体重度 γ=19.2k N/m3。土体平均压缩模量 Es=5MPa，不考虑地下水位的影响。采用单一的土层计算。

　　（2）基坑开挖深度为 9.0m，前后排桩呈矩形布置，桩直径为0.8m，桩弹性模量E1=3.0×107kN/m^2，桩间距为2m，前排桩入土深度为 11m，桩长为 20m。

　　（3）连梁截面尺寸 b×h=800mm×600mm，连梁弹性模量 E2=3.0×107k N/ m^2，连梁之间的距离等于两桩间距，两排桩的排距为 2.0m，桩顶与连梁按刚接考虑。

　　（4）弹簧的反力系数，m=4000kN/m^3，桩底采用单链杆支承约束，以此替代桩土之间摩擦力的作用，水平向不约束。

　　（5）土压力采用朗肯主动土压力计算，并考虑 10k Pa 的地面施工超载，坑底以上为三角形的分布，基坑底面以下为矩形分布。计算弹性地基梁的刚度矩阵相应的代码如下：

%计算弹性地基梁单元刚度矩阵函数
function [Ke] = FrameElementKe2(A,E,I,R,BarLength)
   global m D
   L=BarLength;
   k=m*D*L;
   k1=k;
   k2=k;
   ke=[E*A/L       0             0          -E*A/L       0                0
       0        12*E*I/L^3+4*k1*L/15+k2*L/12     6*E*I/L^2     0       -12*E*I/L^3+k1*L/12+k2*L/15   6*E*I/L^2;
       0        6*E*I/L^2+k1*L^2/30+k2

由于不同基坑开挖深度为9m，所以九米以上的桩可以认为传统梁，九米以下的桩为弹性地基梁。因此在进行单元刚度矩阵计算和组装时要根据单元所在位置分别进行计算和组装，具体的matlab代码如下：

%遍历所有单元，将各单元刚度阵分块组装到总体刚度阵
for iEle =1:EleCount
%该单元的两个节点的编号
n1=ele(iEle,2);n2=ele(iEle,3);
%计算坐标变换矩阵
R=CoordTransform([x(n1) x(n2)],[y(n1) y(n2)],BarLength(iEle));
%计算单元刚度矩阵 Ke=R'*ke*R;局部坐标系下的单元刚度阵转换为全局坐标下的单元刚度阵
if y(n1)<=deep     
ke= FrameElementKe2(ele(iEle,4),ele(iEle,5),ele(iEle,6),R,BarLength(iEle));
else     
ke= FrameElementKe1(ele(iEle,4),ele(iEle,5),ele(iEle,6),R,BarLength(iEle));
end
%将各单元刚度分块组装到总刚相应位置
eleDof=[n1*3-2:n1*3,n2*3-2:n2*3];
K(eleDof,eleDof)=K(eleDof,eleDof)+ke; 
end

　　最终计算得到的前后排桩随深度的挠度和弯矩分别如图3所示，与文献中的结果基本一致，另外本案例还对双排桩支撑结构的弯矩图进行绘制，如图4所示。

　　

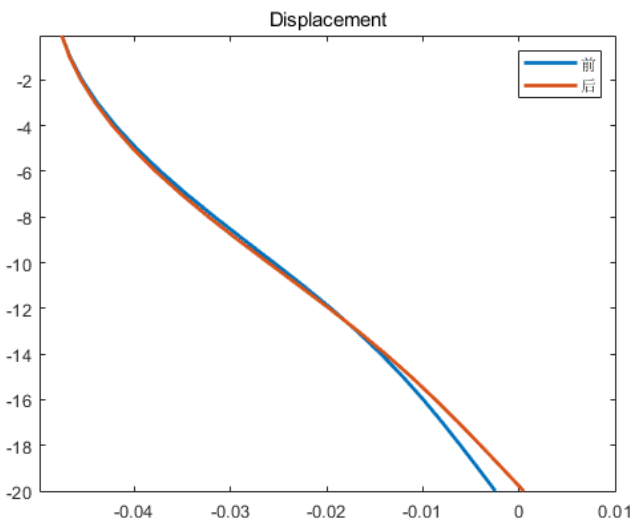
　　图3 前后排桩不同深度处水平位移

　　

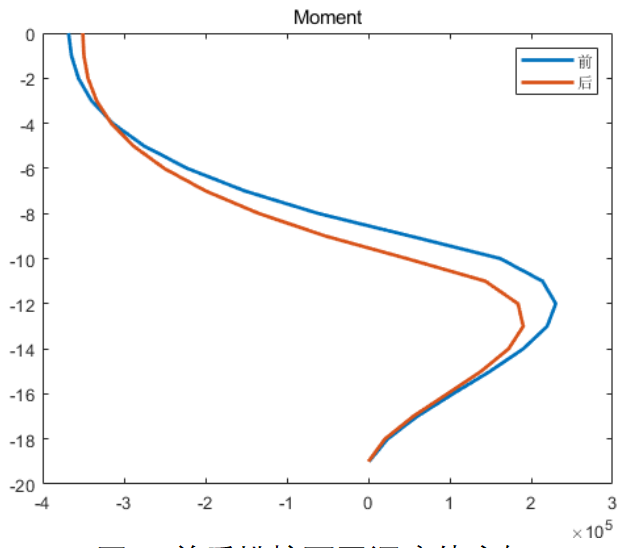
　　图4 前后排桩不同深度处弯矩

　　

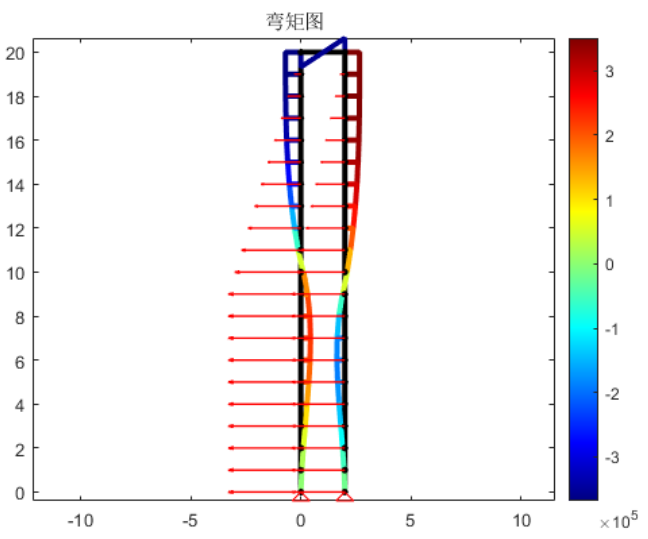
　　图5 弯矩图

　　审核编辑：郭婷