基于改进的二阶振荡粒子群算法的参数估计方法

 引 言

线性调频信号（LFM）在时域和频域上具有理想的多普勒频移和良好的压缩性能，近年来，成为低截获概率雷达信号的一种重要形式，在雷达、声呐及通信等多领域得到了非常普遍的应用。在电子对抗领域中，有许多重要的任务，如电子侦察和电子干扰，可以通过拦截敌方雷达信号和从 LFM 信号中提取参数信息来实现。因此，LFM 信号参数能否准确估计在频谱估计中显得至关重要。

目前，国内外学者在 LFM 信号的参数估计领域做了许多的研究，从时域和频域方面提出了一些可行的参数估计方法。文献[4]提出了基于霍夫变换短时傅里叶变换（STFT）的单源时频域点选择算法，克服了现有算法对频谱重叠 LFM 信号的局限性；文献[5]提出基于自适应粒子群优化（APSO）算法的分段重构（SR）方法，对每个信号部分变换后实现 SR，同时利用互相关指数来表示系统的性能，在信号增强和噪声抑制方面有较好的性能；文献[6]将盒维数理论引入到 LFM 参数估计中，通过探讨信号参数与盒维数的关系来实现参数的估计。但是上面的方法都在一定程度上增加了计算复杂度。文献[7]采用稀疏傅里叶变换，试图从不同的角度降低运算量，但最优旋转角度的判定与选择没有给出定论；文献[8]引入了正交匹配追踪算法，提出了一种估计分数阶带限 LFM 初始频率和最终频率的改进优化算法，但是由于算法所要求的前提条件较多，对信号的估计有一定的限制；文献[9⁃10]提出将基本粒子群算法用于基于分数阶傅里叶变换的 LFM 信号参数估计中，通过改进最优阶次的搜索问题提高了精确度，但本质仍是基于二维峰值搜索的方法，存在计算量和估计精度之间的矛盾。

由于实际的雷达接收机工作时会受到外界环境的影响，因此，本文针对在混合信号中辐射源信号的参数估计问题进行研究，建立辐射源 LFM 相参脉冲串信号模型，提出一种基于二阶振荡粒子群算法和分数域展宽法（W⁃FRFT）相结合的参数估计方法。通过判断鉴相脉冲幅度的变化来识别信号的相参性，区分目标辐射源的信号，在此基础上利用粒子群最优值算法对积累后的信号计算最小分数域展宽值得到 FRFT 的最优阶次，从而求得信号参数。与传统方法相比，本文所提方法解决了最优阶次的精确与否受限于搜索间隔的问题，使精确度和计算复杂度在一定程度上得到了改善。

1 相参脉冲串信号模型

对于接收机接收到的脉冲串信号，可以视作是在不同时刻对连续波信号加以线性调制。接收的 LFM 信号的离散数学模型表示为：

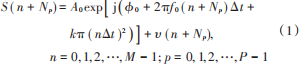
式中：P 为脉冲总个数；f0 为起始频率；A0 为接收信号的幅度；M 为单个脉冲内采样点个数；k 为调频斜率；ϕ0 为恒定的初始相位；Δt 为采样间隔；Np为第 p 个脉冲重复周期内的采样点；υ 为复高斯白噪声干扰信号，实部与虚部噪声相互独立，假设信号为单一重频、幅度不变的线性调频信号。

2 雷达目标辐射源信号识别

在多信息源和多传感器的复杂环境中，目标辐射源的信号往往会受到其他辐射源的干扰或者噪声的影响，需要从测量到的混合信号中提取出目标辐射源信号，进行参数估计，提取有用信息。

雷达辐射源发射的相参脉冲串信号之间的相位具有一致性或连续性，如果脉冲 1 和脉冲 2 来自于同一雷达辐射源，则两个脉冲是相参的，即脉冲 1和脉冲 2的雷达辐射源的初始相位相同[11]；否则，脉冲之间的初始相位不同且信号是非相参的。因此可以根据此理论利用鉴相器的特性，采用时域识别法判别混合信号中的辐射源信号。

假设输入的第 m 个脉冲信号为：

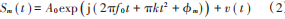
延迟 M 时间后，信号变为：

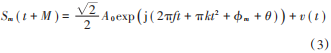
式中，由于延迟造成的附加相位 θ = 2πfM。设延迟时间 M 等于一个脉冲重复间隔，因此当 Sm变成 Sm ( t + M ) 时，原信号 Sm 的下个脉冲刚好到达混频器：

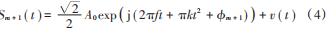
当式（3）和式（4）中 2 路信号进入混频器后，对此进行共轭相乘运算，共轭相乘后的信号经过低通滤波器。

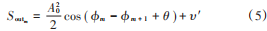
由于相参脉冲信号满足初始相位均相同的特性，因此，若是来自同一辐射源的相参信号，则鉴相器输出的鉴相脉冲幅度的实部为：

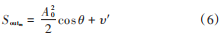
由于输出的幅度实部与延迟造成的附加相位 θ、幅度 A0 和噪声项有关，而前两者均为恒定不变的值，因此P 个脉冲组成的脉冲串输出的 P-1 个鉴相脉冲幅度仅仅噪声组合项不同，而噪声是均值相同的高斯白噪声，所以式（6）输出的幅度近似相同，脉冲幅度在 0.5上下轻微波动。而若脉冲串为非相参的脉冲信号，相位差为一个周期内的随机量，则鉴相脉冲幅度会随着相位差的随机变化而在 0~0.5 范围内波动起伏，且有明显峰值。信号相参性时域识别法的具体识别流程图如图 1所示。

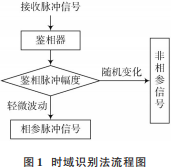
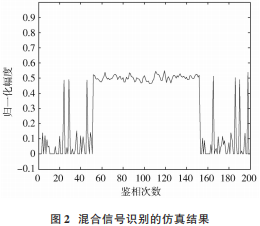
以一个混合信号脉冲串为例，其中前 50 个脉冲和后 150个脉冲为非相参信号，51~149个脉冲为来自目标辐射源的相参信号。

如图 2 仿真曲线所示，脉冲串信号通过鉴相判别，将相参信号和非相参信号通过幅度值范围区分开来，可以看出，非相参信号脉冲串幅度值不仅波动范围大，而且有明显峰值，而相参信号脉冲串幅度值一直呈现平稳状态，证明此方法对于识别目标辐射源相参信号有效。通过对接收到的混合信号进行判别，可以准确获得目标辐射源的信号，有利于后续的参数估计，获得有效信息。

3 目标辐射源信号的参数估计

3.1 LFM 信号的 FRFT表示

在第 2 节中通过对混合脉冲信号进行时域相参识别的处理，分离得到辐射源相参脉冲信号，对该脉冲信号进行时域积累后进行参数估计。假定时域积累后脉冲宽度内的 LFM 信号的复数表达式如下：

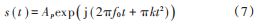
s ( t )的 FRFT的定义式为：

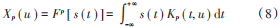
式中：p 是 FRFT 阶次；Fp 是 FRFT算子；Kp(t,u)是 FRFT核[12]，表示为：

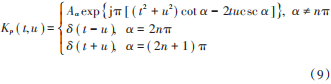
式中 Aα = 1 - jcot α ，α = pπ 2 为时频平面的变换角度，取值范围可以为任意实数。

LFM 信号在变换域上的分布如图 3所示。

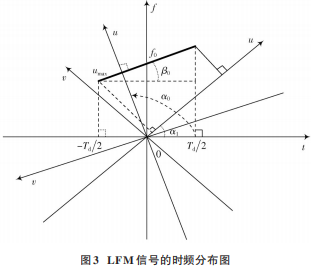
在图 3 中，黑色斜线表示 LFM 信号的时频分布线，β（0β0 ∈ ( 0, π 2 ) 或 β0∈（π 2，π））为时频线与 t 轴的夹角，u ⊥ v 轴表示时、频轴逆时针旋转 α 角度，此处取 α∈[0，π]，由 α 和 p 的变换关系可得 p∈[0，2]。随着旋转角度α 的变化，FRFT 会形成一个时频平面的变化，且不同的旋转角度会带来不同的聚集特性，包括频谱在分数域内的宽度、频谱的幅值等，但不变的性质是信号只在其匹配的最佳分数域内出现频谱尖峰。

3.2 基于 FRFT的分数域展宽（W⁃FRFT）

由于 LFM 信号观测时长为 Tp，信号的时频线与时间轴 t的角度为 β0，则 LFM 信号的时频线长度 ρ为[13]：

由式（10）可知，信号参数 Tp 和 β0 已知时，时频线长度 ρ 是一个常量。当时频线在分数域上旋转 α 角度后，在 u 轴上的投影为 ρα，即分数域展宽值。此时设时频线与 u 轴的夹角为 θ=β- α，其中取 β∈（0，π 2），此时，信号的分数域展宽值为：

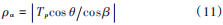
因此，当信号确定时，LFM信号的分数域展宽值是一个仅与旋转角度α相关的值。α角度的变化影响时频线在 u 轴的投影，当 α = β 时，ρ⫽u，此时，ρα 取得最大值；当 α =β+π2时，ρ ⊥ u，ρα 取得最小值，且 ρα趋近于0，此时α为最佳旋转角度，对应的p为最优阶次。

文献[14]中为保持时域和频域上的一致性，降低精度误差，需要对 LFM 信号进行归一化处理，设维度归一化因子为S=(Tp fs1 2)，则初始频率和调频斜率的估计值为：

3.3 降低分数阶次以减小计算量

根据式（12），可得：

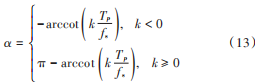
由奈奎斯特采样定理可得，采样频率 fs 至少是带宽B 的 2 倍，为了得到无失真的原始信号，采样频率 fs 必须满足[15]：

将式（14）代入式（13）可得：

由于 α = pπ 2，所以式（15）可化为：

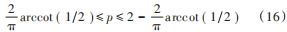
因此，FRFT 阶次 p 从[0，2]缩小到[0.7，1.29]，与传统的 FRFT方法相比，节省了 2 3左右的计算量。

4 基于二阶振荡粒子群算法和W⁃FRFT的LFM信号参数估计方法

基于 W⁃FRFT算法进行最优阶次 p求解时，需要对 p进行搜索，搜索间隔越小，误差越小，估计精度越高，则所需时间越长，反之，则造成参数估计误差越大。因此，本文通过粒子群算法对基于分数展宽原理的参数估计进行改进，避免因搜索间隔问题而不能准确找到最优解的情况。以分数域展宽值为目标适应度函数，以阶次[0.7，1.29]为位置范围，在位置范围内寻找最小分数域展宽值，从而得到对应的最优阶次。

标准粒子群算法中种群进化是由粒子的速度公式和位置公式组成：

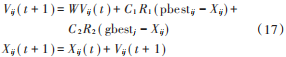
式中：Xij 和 Vij 分别是第 i 个粒子所处的位置和速度的第 j 维；pbestij 为第 i 个粒子在历史最优位置时的第 j 维；gbestj 为全局最优位置的第 j 维[16]；W 为惯性权重；C1 和C2 分别为调节粒子自身最优位置和全局历史最优位置靠近的权重；R1和 R2为相互独立的随机数。

但是标准粒子群算法中所有粒子的更新仅仅依靠它的个体最优位置和全局最优位置，并没有考虑到粒子个体之间及粒子位置变化对它自身的影响，使得粒子没有充分利用有效信息。

本文将改进的二阶振荡粒子群算法引入到信号处理中，针对分数域中最优阶次的搜索进行改进，改进后的粒子群算法的迭代公式如下：

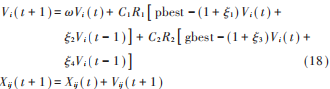
这里的 ξi, i = 1, 2, 3, 4 虽然是随机数，但是取值是有限制的，设最大迭代次数为Gmax：

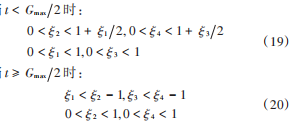
同时，为了防止后期局部搜索能力变差，陷入局部最优等问题，对惯性权重进行改进[17]，并表示为：

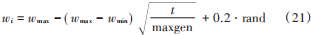
式中 maxgen 为最大迭代次数。改进后的参数估计算法充分利用了所有粒子的最优位置的有效信息及同一粒子的位置变化信息，更加精确地搜索到最优阶次，避免了搜索间隔带来的误差，同时，减小了计算量，进一步提高了算法的优化性能。

基于二阶振荡粒子群算法与 W ⁃FRFT 相结合的优化算法流程如下：

1）在混合信号中根据雷达辐射源发射信号的相参性识别出目标辐射源的信号；

2）经过时域积累后的信号在缩小后的阶数范围[0.7，1.29]内，初始化粒子的位置并计算粒子的适应度值，即分数域展宽值；

3） 寻 找 粒 子 的 全 局 极 值 并 更 新 粒 子 的 位 置 和速度；

4）判断是否满足精度要求和迭代次数，如果不满足，则回到步骤 3）；

5）若适应度值满足精度要求和迭代次数，则输出最小适应度值即最小分数域展宽值和最优阶次，根据式（12）计算初始频率 f和调频斜率 k。

5 仿真实验与结果分析

本文以接收宽带 LFM 信号为例，其初始频率 f0 =100 MHz，采样频率 fs =2.4 GHz，振幅 Ap = 1，脉冲宽度Tp=1 μs，带宽 B =500 MHz，调频斜率 k = B Tp。

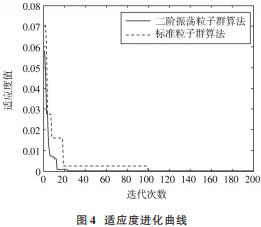
分别对两种粒子群算法改进的参数估计算法进行比较：二阶振荡粒子群优化算法中选取粒子数为 50，迭代次数为 200；标准粒子群优化算法选取粒子数为 60，迭代次数为 200，其他参数均相同。

从图 4 中可以看出，即使在粒子数较少的条件下，振荡粒子群算法在迭代 22 次左右就已经趋向于稳定，而标准粒子群算法在 100 次之后才能达到近似相同的适应度值。

在高斯噪声条件下，分别对不同的算法进行计算精度分析。在信噪比为-15~5 dB 范围内，分别采用峰值搜索、标准粒子群算法与二阶振荡粒子群算法进行参数估计，每间隔 1 dB 进行 100 次蒙特卡洛仿真实验，计算参数估计的均方误差，衡量算法的计算精度。其中，相对误差的定义为：

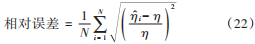
式中：η 和 ηi分别为参数实际值和第 i 次的估计值；N 为蒙特卡洛实验仿真次数。

调频斜率和初始频率的均方根误差与信噪比的关系分别如图 5和图 6所示。

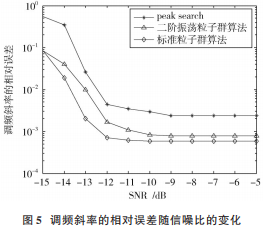
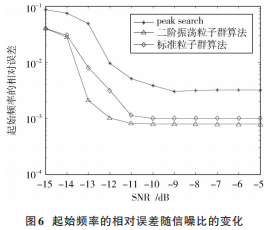
在低信噪比时，二维峰值搜索算法比较依赖于信噪比，相对误差较大，随着信噪比的增加，在高信噪比时相比于改进的算法有较小的相对误差。文献[9]中基于粒子群算法和 FRFT 的算法相对于传统算法有一定的改进，但是基于二阶振荡粒子群算法和 W ⁃FRFT 的算法在低信噪比时的相对误差更低，且测量误差在千赫兹以内。由于幅相失真条件更复杂，参数估计性能会下降。

6 结 论

针对混合信号中的目标辐射源的识别和参数估计精度与搜索间隔存在矛盾的问题，本文提出一种二阶振荡粒子群算法与 W⁃FRFT 算法相结合的 LFM 信号检测方法。仿真结果表明，本文方法可以准确识别出辐射源的信号，且当其他实验条件相同时，在信噪比为-9 dB的条件下，相比于其他粒子群改进算法，本文算法的迭代过程能更快趋向于稳定，且相对误差与峰值搜索算法相差 10-1数量级。

审核编辑：郭婷