简单总结几种NLP常用的对抗训练方法

对抗训练本质是为了提高模型的鲁棒性，一般情况下在传统训练的基础上，添加了对抗训练是可以进一步提升效果的，在比赛打榜、调参时是非常重要的一个trick。对抗训练在CV领域内非常常用，那么在NLP领域如何使用呢？本文简单总结几种常用的对抗训练方法。

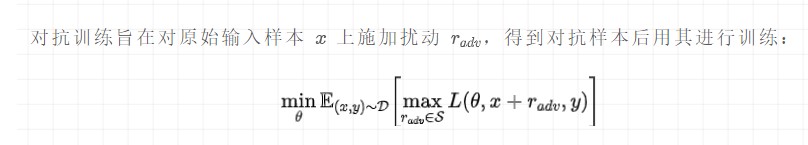
公式理解：

最大化扰动：挑选一个能使得模型产生更大损失（梯度较大）的扰动量，作为攻击；

最小化损失：根据最大的扰动量，添加到输入样本后，朝着最小化含有扰动的损失（梯度下降）方向更新参数；

这个被构造出来的“对抗样本”并不能具体对应到某个单词，因此，反过来在推理阶段是没有办法通过修改原始输入得到这样的对抗样本。

对抗训练有两个作用，一是 提高模型对恶意攻击的鲁棒性 ，二是 提高模型的泛化能力 。

在CV任务，根据经验性的结论，对抗训练往往会使得模型在非对抗样本上的表现变差，然而神奇的是，在NLP任务中，模型的泛化能力反而变强了。

常用的几种对抗训练方法有FGSM、FGM、PGD、FreeAT、YOPO、FreeLB、SMART。本文暂时只介绍博主常用的3个方法，分别是 FGM 、 PGD 和 FreeLB 。

具体实现时，不同的对抗方法会有差异，但是 从训练速度和代码编辑难易程度的角度考虑，推荐使用FGM和迭代次数较少的PGD 。

一、FGM算法

FGM的代码量很少，只需要自行实现简单的类即可：

 

import torch
class FGM():
    def __init__(self, model):
        self.model = model
        self.backup = {} # 用于保存模型扰动前的参数

    def attack(
        self, 
        epsilon=1., 
        emb_name='word_embeddings' # emb_name表示模型中embedding的参数名
    ):
        '''
        生成扰动和对抗样本
        '''
        for name, param in self.model.named_parameters(): # 遍历模型的所有参数 
            if param.requires_grad and emb_name in name: # 只取word embedding层的参数
                self.backup[name] = param.data.clone() # 保存参数值
                norm = torch.norm(param.grad) # 对参数梯度进行二范式归一化
                if norm != 0 and not torch.isnan(norm): # 计算扰动，并在输入参数值上添加扰动
                    r_at = epsilon * param.grad / norm
                    param.data.add_(r_at)

    def restore(
        self, 
        emb_name='word_embeddings' # emb_name表示模型中embedding的参数名
    ):
        '''
        恢复添加扰动的参数
        '''
        for name, param in self.model.named_parameters(): # 遍历模型的所有参数
            if param.requires_grad and emb_name in name:  # 只取word embedding层的参数
                assert name in self.backup
                param.data = self.backup[name] # 重新加载保存的参数值
        self.backup = {}

 

在训练时，只需要额外添加5行代码：

 

fgm = FGM(model) # （#1）初始化
for batch_input, batch_label in data:
    loss = model(batch_input, batch_label) # 正常训练
    loss.backward() # 反向传播，得到正常的grad
    # 对抗训练
    fgm.attack() # （#2）在embedding上添加对抗扰动
    loss_adv = model(batch_input, batch_label) # （#3）计算含有扰动的对抗样本的loss
    loss_adv.backward() # （#4）反向传播，并在正常的grad基础上，累加对抗训练的梯度
    fgm.restore() # （#5）恢复embedding参数
    # 梯度下降，更新参数
    optimizer.step()
    model.zero_grad()

 

二、PGD算法

Project Gradient Descent（PGD）是一种迭代攻击算法，相比于普通的FGM 仅做一次迭代，PGD是做多次迭代，每次走一小步，每次迭代都会将扰动投射到规定范围内。形式化描述为：

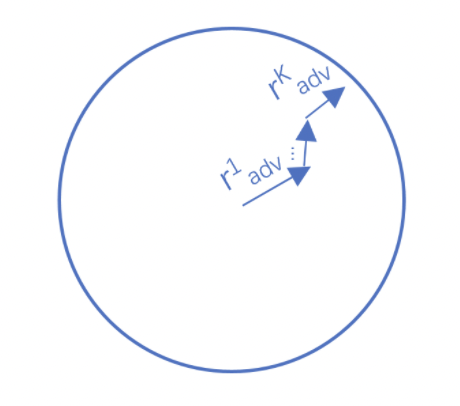
代码实现如下所示：

 

import torch
class PGD():
    def __init__(self, model):
        self.model = model
        self.emb_backup = {}
        self.grad_backup = {}

    def attack(self, epsilon=1., alpha=0.3, emb_name='word_embeddings', is_first_attack=False):
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                if is_first_attack:
                    self.emb_backup[name] = param.data.clone()
                norm = torch.norm(param.grad)
                if norm != 0 and not torch.isnan(norm):
                    r_at = alpha * param.grad / norm
                    param.data.add_(r_at)
                    param.data = self.project(name, param.data, epsilon)

    def restore(self, emb_name='word_embeddings'):
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name: 
                assert name in self.emb_backup
                param.data = self.emb_backup[name]
        self.emb_backup = {}

    def project(self, param_name, param_data, epsilon):
        r = param_data - self.emb_backup[param_name]
        if torch.norm(r) > epsilon:
            r = epsilon * r / torch.norm(r)
        return self.emb_backup[param_name] + r

    def backup_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                self.grad_backup[name] = param.grad.clone()

    def restore_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                param.grad = self.grad_backup[name]

pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
    # 正常训练
    loss = model(batch_input, batch_label)
    loss.backward() # 反向传播，得到正常的grad
    pgd.backup_grad()
    # 累积多次对抗训练——每次生成对抗样本后，进行一次对抗训练，并不断累积梯度
    for t in range(K):
        pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
        if t != K-1:
            model.zero_grad()
        else:
            pgd.restore_grad()
        loss_adv = model(batch_input, batch_label)
        loss_adv.backward() # 反向传播，并在正常的grad基础上，累加对抗训练的梯度
    pgd.restore() # 恢复embedding参数
    # 梯度下降，更新参数
    optimizer.step()
    model.zero_grad()

 

三、FreeLB算法

很明显找到FreeLB与PGD的区别在于累积的方式：

FreeLB：通过对 K K K 次梯度的平均累积作为扰动更新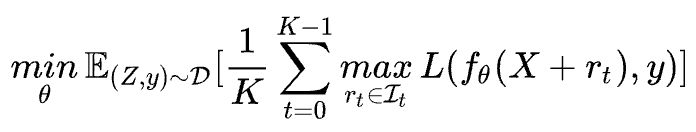

PGD：只取最后一次的梯度进行更新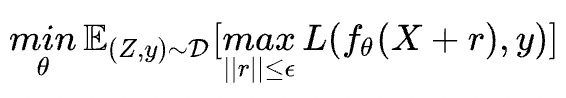

实现流程如下图所示：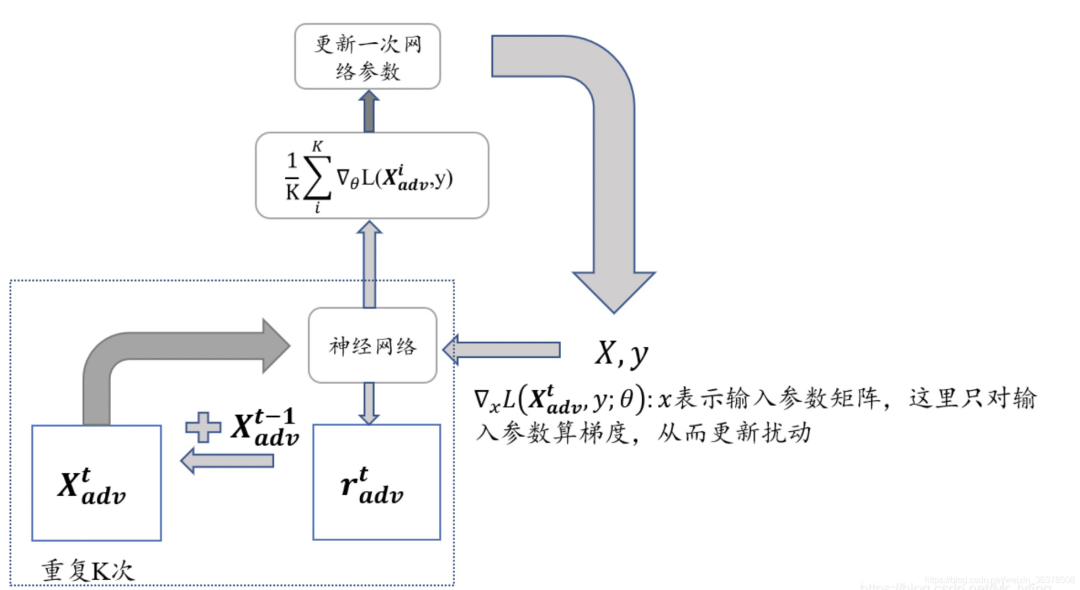

审核编辑：刘清