LC振荡电路原理详解

给大家分享一下关于LC振荡电路。LC振荡器的类型有很多，例如：哈特利振荡器、Colpitts 振荡器、克拉普振荡器等

什么是LC振荡电路?

LC 振荡电路是指由电感 L 和电容 C 组成选频网络，用于产生高频正弦波信号的电路。

在许多情况下，LC 振荡电路也称为振荡器电路、谐振电路、谐振电路或调谐电路。

常见的 LC 正弦波振荡电路有变压器反馈式 LC 振荡电路和电感三点 LC 振荡电路和电容三点 LC 振荡电路。

LC 振荡电路的辐射功率与振荡频率的四次方成正比，允许振荡 LC 电路辐射足够强的电磁波，必须提高振荡频率，电路呈开路形式。

LC 振荡器使用一个振荡电路(包括一个电感和一个电容)，它提供所需的正反馈以维持电路中的振荡。顾名思义，在这个电路中，一个充电的电容( C) )连接到一个未充电的电感( L )，如下图所示。

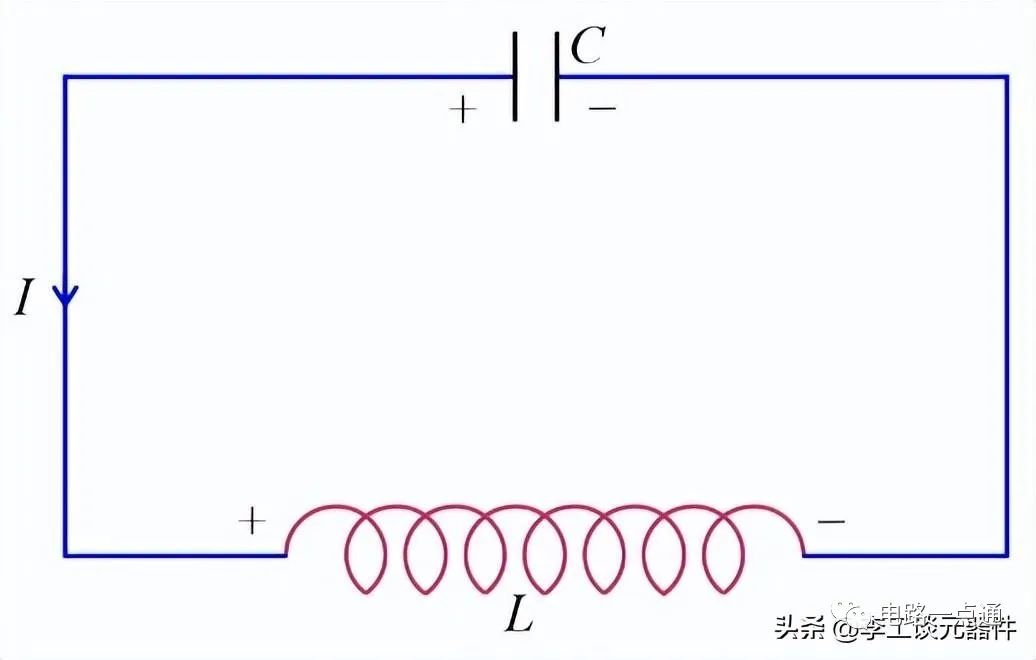
LC谐振电路

上面显示的电路是一个 LC 谐振电路，该电路包含一个完全充电的电容和一个完全断电的电感，该电感的电阻必须尽可能低(理想情况下为零)。

如果将充电的电容连接到电阻，则电容的能量将被电阻器消耗，电流最终会停止流动。

但在这种情况下，这个电容(存储电能)连接到一个电阻非常低的电感(存储磁能)。因此，随着电感开始从电容中获取能量，它开始通电，并且其能量增加，这反过来又使电容放电。

当电感完全通电时，电容失去所有能量。电感将通过存储在其中的能量开始为电容充电。从电容到电感以及从电感到电容的能量转移继续进行。

这种从一个设备到另一个设备的持续能量转移就是常说的 LC 振荡，下图为LC振荡器原理动图。

LC振荡电路原理动画

LC振荡电路原理作用

当一个完全通电的电容连接到一个断电的电感时，整个电路的所有能量都只在电容上，而电感的能量为零。

我们将存储在电容中的能量(电能)表示为 (U_E)，将存储在电感中的能量(磁能)表示为 (U_B)。下图描述了LC振荡电路图原理。

LC振荡电路原理图

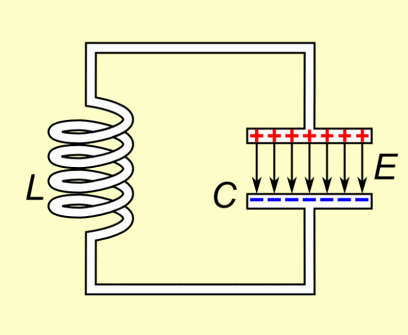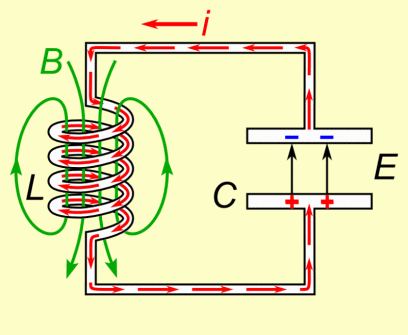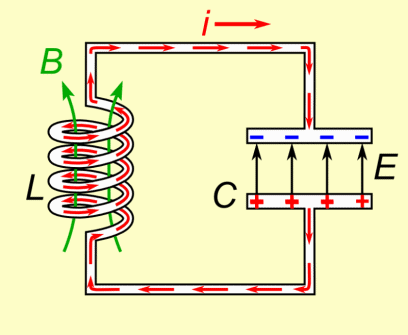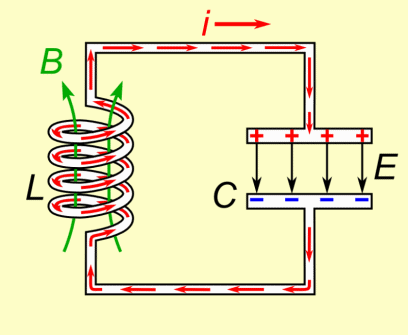
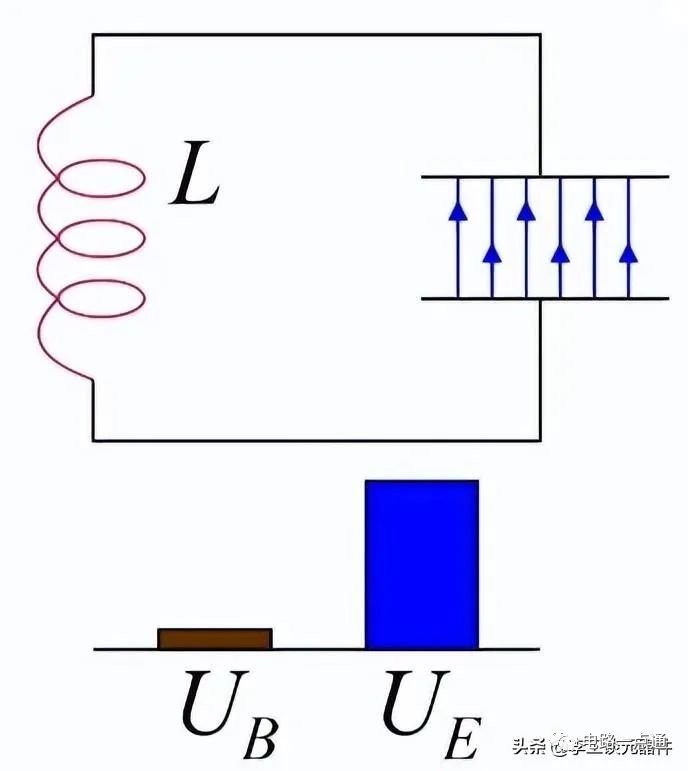
电流开始从电容流向电器，电感开始通电，电开始放电。电感的能量开始增加，电容的能量开始减少。下图描述了LC振荡电路图原理。

电路图下方的条形图显示，此时，电感中存储的能量有一半等于电容的能量，这意味着电容已将一半的能量转移到了电感中。

LC振荡电路原理图

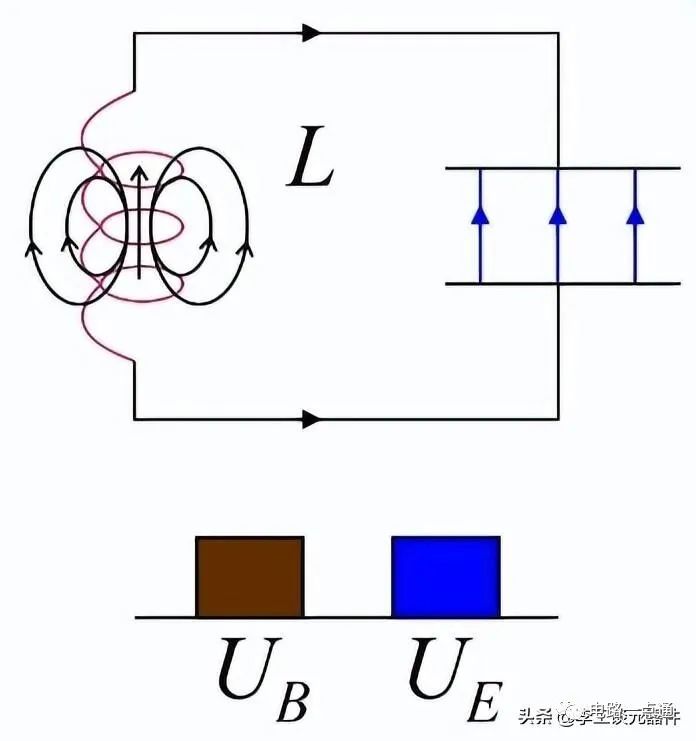
现在，一旦电容完全放电，电容的所有能量都将转移到电感。因此，全部电能都转化为磁能。下图描述了LC振荡电路图原理。

LC振荡电路图原理图

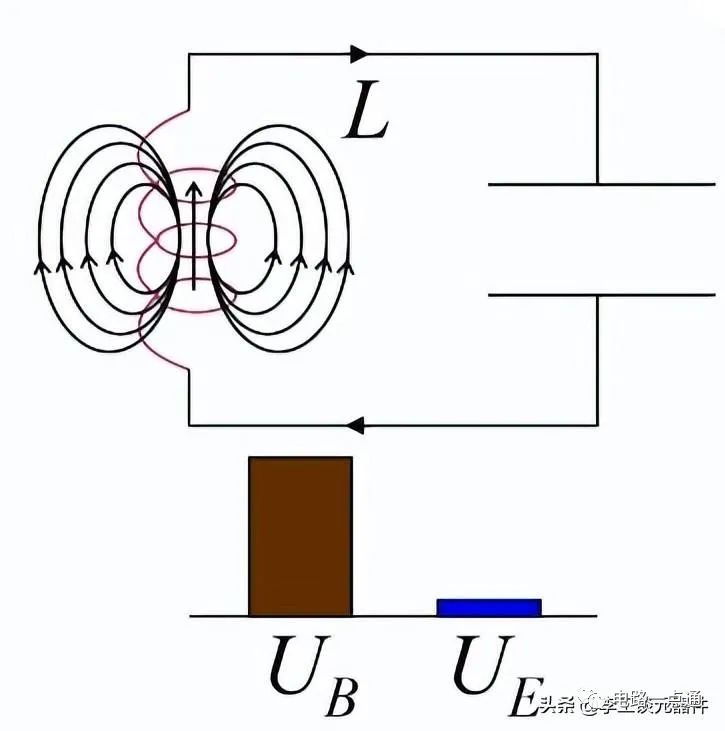
由于电容完全放电并且电感完全通电，现在电感将以相同方向的电流开始对电容充电。下图描述了LC振荡电路图原理。

现在电感已经将一半的能量转移到了电容上。

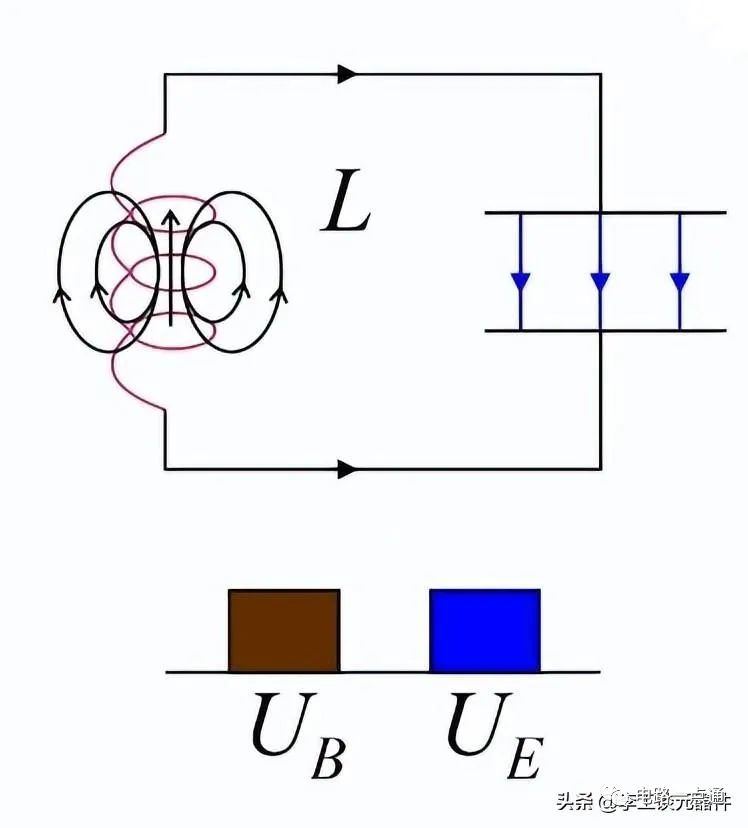
LC振荡电路图原理

最后，电容将再次充满电，电感将完全通电。但是现在电容的不同之处在于它的极性是相反的。下图描述了LC振荡电路图原理。

因此，如果电流再次从电容开始在电路中流动，它将以相反的方向流动。由于电路中的电流现在具有相反的电流，我们可以说它已经完成了交流周期的前半部分并开始了后半部分。

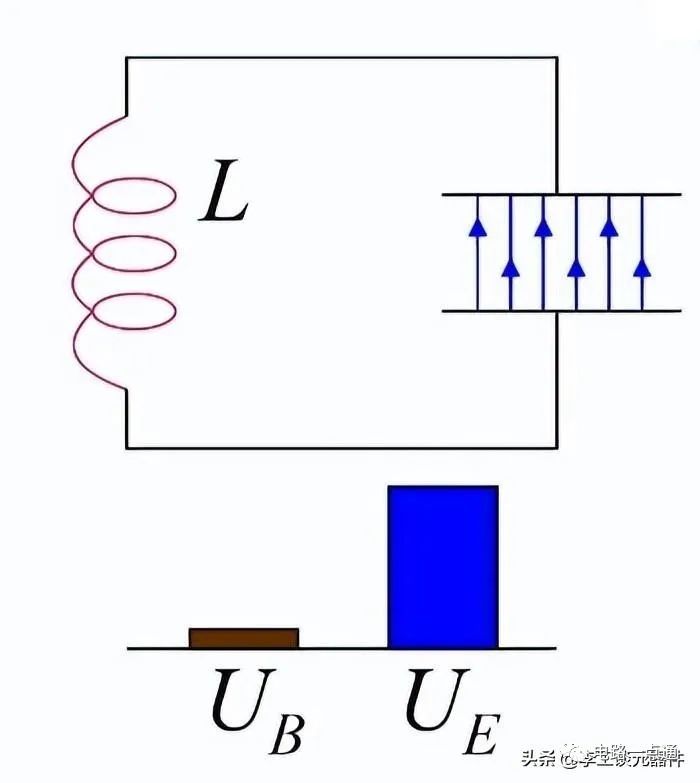
LC振荡电路图原理

因此，当整个周期完成时，电容和电感都将完全充电两次。

基本 LC 振荡电路

下图的电路由一个感应线圈 L 和一个电容 C 组成。

电容以静电场的形式储存能量，并在其极板上产生电位(静电压)，而感应线圈以电磁场的形式储存能量。通过将开关置于位置 A ，电容充电至直流电源电压 V。当电容充满电时，开关切换到位置B。

充电的电容现在并联在感应线圈上，因此电容开始通过线圈自行放电。随着通过线圈的电流开始上升， C两端的电压开始下降。

这种上升的电流在线圈周围建立了一个电磁场，该电磁场抵抗了这种电流的流动。当电容 C 完全释放了最初存储在电容中的能量时，C 作为静电场现在存储在感应线圈中，L 作为线圈绕组周围的电磁场。

由于现在电路中没有外部电压来维持线圈内的电流，因此随着电磁场开始崩溃，电流开始下降。在线圈中感应出一个反电动势 ( e = -Ldi/dt )，使电流保持在原始方向上流动。

该电流以与其原始电荷相反的极性为电容 C 充电。C 继续充电，直到电流减小到零，线圈的电磁场完全崩溃。

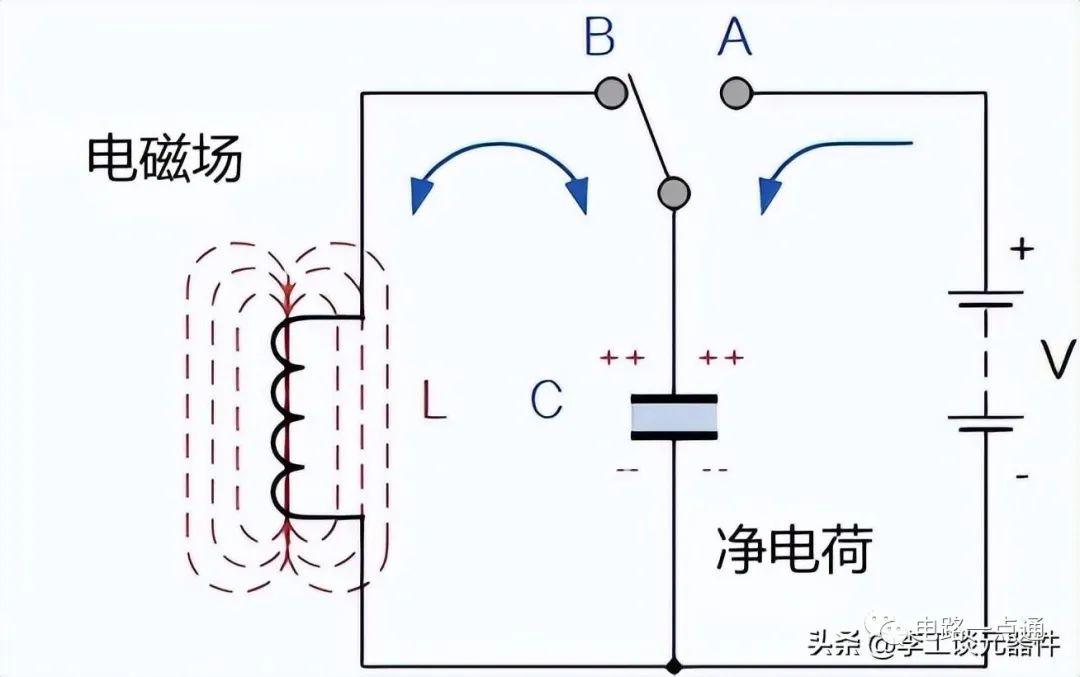
LC振荡电路

最初通过开关引入电路的能量已返回到电容，电容上再次具有静电电压电位，尽管它现在具有相反的极性。电容现在开始通过线圈再次放电，并重复整个过程。当能量在电容和电感之间来回传递时，电压的极性会发生变化，从而产生交流型正弦电压和电流波形。

此过程形成 LC 振荡电路的基础，理论上这种来回循环将无限期地继续。然而，事情并不完美，每次能量从电容 C 传输到电感器 L 并从L传输回 C 时，都会发生一些能量损失，随着时间的推移，振荡衰减为零。

如果不是因为电路内的能量损失，这种在电容 C 到电感 L 之间来回传递能量的振荡作用将无限期地持续下去。电能在直流或电感线圈的实际电阻中、电容的电介质中以及电路的辐射中丢失，因此振荡稳定地减小，直到它们完全消失并且过程停止。

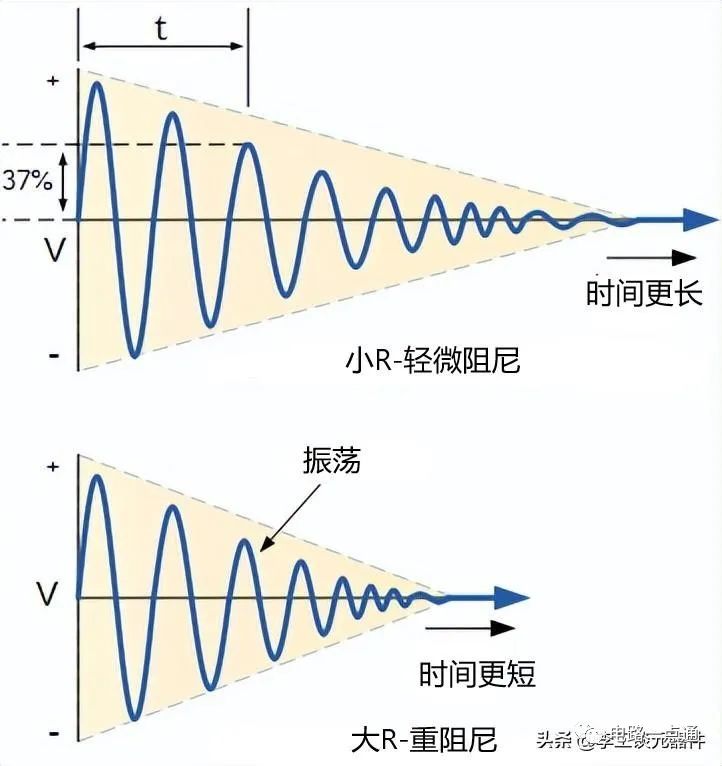
在实际的 LC 电路中，振荡电压的幅度在每半个振荡周期都会减小，最终会消失到零。然后将振荡称为“阻尼”，阻尼量由电路的质量或 Q 因子决定。

LC振荡电路--阻尼振荡

振荡电压的频率取决于LC谐振电路中的电感值和电容值。我们现在知道，谐振电路中要发生谐振，必须有一个频率点，即X C 的值，容抗与X L的值相同，感抗 ( X L = X C ) 和因此，这将相互抵消，只留下电路中的直流电阻来阻止电流流动。

LC振荡电路--共振频率

如果我们现在将电感的感抗曲线放在电容容抗曲线的顶部，使两条曲线在相同的频率轴上，交点将为我们提供谐振频率点，( ƒ r或ωr ) 如下图所示。

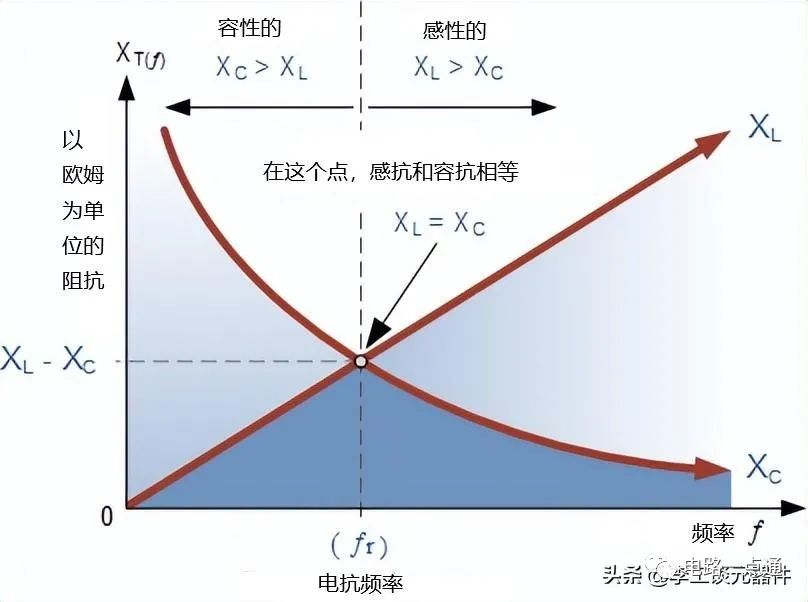
LC振荡频率

其中：ƒ r以赫兹为单位，L以亨利为单位，C以法拉为单位。

那么发生这种情况的 LC 振荡频率公式如下：

LC振荡频率公式

然后通过简化上述等式，我们得到调谐LC电路中谐振频率ƒ r的最终等式：

LC振荡电路--LC 振荡频率公式

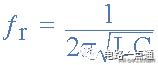
LC频率振荡公式

L 是以亨利为单位的电感

C 是以法拉为单位的电容

ƒ r 是以赫兹为单位的输出频率

这个等式表明，如果L或C减小，频率就会增加。该输出频率通常以 ( ƒ r ) 的缩写形式给出，以将其标识为“谐振频率”。

为了保持 LC 谐振电路中的振荡，我们必须替换每个振荡中损失的所有能量，并将这些振荡的幅度保持在恒定水平。因此，替换的能量量必须等于每个循环期间损失的能量。

如果替换的能量太大，幅度会增加，直到发生电源轨削波。或者，如果被替换的能量太小，幅度最终会随着时间的推移而减小到零，并且振荡会停止。

替代这种损失能量的最简单方法是从 LC 谐振电路获取部分输出，将其放大，然后再次将其反馈回 LC 电路。

基本晶体管 LC 振荡器电路

上述过程可以使用电压放大器来实现，该电压放大器使用运算放大器、FET 或双极晶体管作为其有源器件。然而，如果反馈放大器的环路增益太小，所需的振荡衰减为零，如果太大，波形就会失真。

为了产生恒定的振荡，必须精确控制反馈到 LC 网络的能量水平。然后，当幅度试图从参考电压向上或向下变化时，必须有某种形式的自动幅度或增益控制。

为了保持稳定的振荡，电路的总增益必须等于 1 或 1。再少一点，振荡就不会开始或消失到零，再多一点振荡就会发生，但幅度将被电源轨削波，从而导致失真。如下图所示。

晶体管 LC振荡电路

双极晶体管用作 LC 振荡器放大器，调谐 LC 谐振电路用作集电极负载。另一个线圈L2连接在晶体管的基极和发射极之间，其电磁场与线圈L的电磁场“相互”耦合。

基本晶体管 LC 振荡器电路工作原理

两个电路之间存在“互感”，一个线圈电路中流动的变化电流通过电磁感应在另一个电路中感应出电位电压(变压器效应)，因此在调谐电路中发生振荡，电磁能量从线圈转移 L 到线圈 L2，并且在晶体管的基极和发射极之间施加与调谐电路中频率相同的电压。以这种方式，必要的自动反馈电压被施加到放大晶体管。

可以通过改变两个线圈 L 和 L2 之间的耦合来增加或减少反馈量。当电路振荡时，它的阻抗是电阻性的，集电极和基极电压相差 180 度。为了保持振荡(称为频率稳定性)，施加到调谐电路的电压必须与调谐电路中发生的振荡“同相”。

因此，我们必须在集电极和基极之间的反馈路径中引入一个额外的 180 度相移。这是通过以相对于线圈L的正确方向缠绕L2的线圈来实现的，从而为我们提供振荡器电路的正确幅度和相位关系，或者通过在放大器的输出和输入之间连接相移网络来实现。

因此，LC 振荡器是更常见的“正弦振荡器”或“谐波振荡器”。LC 振荡器可以产生高频正弦波，用于射频 (RF) 类型的应用，晶体管放大器是双极晶体管或 FET。

谐波振荡器有许多不同的形式，因为有许多不同的方法来构建 LC 滤波器网络和放大器，最常见的是哈特利振荡器、Colpitts 振荡器、克拉普振荡器、Armstrong 振荡器等。有的已经详细讲过了，大家可以点击下方标题直接跳转。

LC 振荡电路示例

一个 200mH 的电感和一个 10pF 的电容并联在一起，形成一个 LC 振荡回路。计算振荡频率。

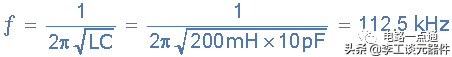
可以从上面的例子中看到，通过减小电容C 或电感 的值，L 将具有增加 LC 振荡电路振荡频率的效果。

LC振荡电路的优点

高相位稳定性 LC 振荡电路在高频下产生良好的稳定性。

低噪声，这是由于反馈网络中的电感和电容。

高品质因数 与其他振荡器相比，LC 振荡器具有高品质因数。

LC振荡电路的缺点

温度的变化会影响元件，例如晶体管、电容、电阻、电源电压和电路的电感。

振荡器的工作频率不是恒定，这是由于电路中涉及的各种组件。

如果反馈电路中的任何组件发生变化，工作频率可能会发生变化。

它不适用于低频。在低频时，电容和电感不能很好地工作并在电路中产生不稳定。

　　审核编辑：汤梓红