Seam Carving一种很强的图像缩放算法

Seam Carving一种很强的图像缩放算法

0

简介

我们在排版的时候可能会遇到一些尴尬的情况。一张图片原本是竖着的，而你希望把它当作一张宽屏图片，于是你只好对它进行拉伸：

抚子的形状瞬间变得不可描述起来。有没有什么办法，能不改变前景抚子的形象，只是拉伸背景的天空呢？也许你会想到万能的神经网络。但早在神经网络火遍大江南北之前，就有一种方法流行于世间：Seam Carving。它可以做到这样：

完美符合我们的要求！那么这个仿佛魔法一样的Seam Carving是如何工作的呢？

01

什么是图像

我们这里将所谈论到的图像限定为二维的像素图象，而不是矢量图象或者三维的体素组成的“图像”之类的东西。对于一幅图像，它的每个像素拥有一个整数坐标，同时拥有一个颜色，后者以 RGB 的形式表现。

当人看到图像的时候，主要是通过识别图像当中的边缘来分辨图像中的物体的，这提示我们边缘的信息对于寻找图像中的主要物体有着重要的作用。如果我们在图像缩放的时候能够尽量不影响到这些像素，那么就有可能做到在保证图像中主要物体的比例不变的情况下拉伸背景。就像这样

|  原图像

|  缩放后

由此我们可以得出结论：通过依次删除图像中若干条自上而下和自左而右的像素通路，就可以达到“缩放”的目的。就自上而下的像素通路来说，这样的通路宽度为 1，从图像的第一行连接到图像的最后一行，在每一行中只占据一个像素，相邻行的像素的水平坐标相差在 -1 到 1 之间。删除这样的自上而下的像素保证了图像的宽度减一的同时不会出现宽度不同的行；自左而右的像素通路也是同理。

图中的红线分别是一条垂直通路和水平通路。如何找到这样的像素通路，穿过尽可能少的重要物体？为此，我们引入了一个概念：“能量”。

02

能量，又是能量

能量在这里起到的作用是表征像素的重要程度。先从图像的基本元素的能量——像素的能量说起。对于单个像素，我们可以定义其能量形式为：

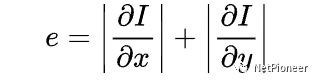
其中，字母I表示像素灰度值，第一个偏导项就表示了色彩在这个像素变化的剧烈程度。如果我们将 RGB 颜色的像素的颜色看作一个三维向量，那么其能量形式也会是一个三维向量，这对于算法的后续实现是不利的。在实现中，我们可以用灰度标量代替 RGB 三维向量参与运算，因为人眼对灰度的敏感度远高于色彩。公式看起来不太直观，来看一个例子：

与人物有关的部分，细节比较多，对应的颜色变化也更明显，能量也就越高。相比之下，背景部分比如天空的颜色变化不太明显，能量普遍比较低。对应到上图中，可能找到的垂直能量通路就是左侧的天空，删除之后并不会影响鱼和人物的部分。

对于任意的一条自上而下的像素通路，该通路的能量就是该通路中所有像素的能量的和。

03

利用能量进行分割

前文说到，像素的能量表征了像素的重要程度，那么像素通路的能量就表征了像素通路中所有像素的总体重要程度，也就表征了该通路穿过的重要物体的多寡，也就表征了删除这条像素通路对图像中重要物体的影响程度的大小。删除一条能量最小的像素通路对图像中重要物体的影响是最小的。

对于这样一张图像，如果对其进行缩放，我们希望保留不同颜色间的分界线，使其形状和比例尽可能地不改变。即这几条分界线的重要性应该尽可能地高。根据我们关于能量的定义，分界线附近的像素的能量显著地高于色块中的像素。如果要被删去的像素通路主要通过色块区域，那么分界线的形状就可以得到保留了。

那么现在的问题就变成了如何寻找一条能量最小的像素通路，这里以自上而下的像素通路说明寻找这样的像素通路的方式。这就转换为了一个经典的动态规划问题，形式化的转移方程如下：

我们记 dpi 为从图像的第一行到第 i 行的第 j 个像素的通路中能量最小的通路的能量 e 以及该像素在该通路上的前驱 p。第 i 行的第 j 个像素的能量为 e(i,j)。那么

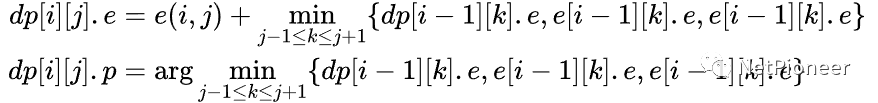
这个公式可能还是有点太过抽象了。由于通路一定是连通的，也就是某一个像素只可能与三个像素位于同一条通路内，分别是它的左上、正上和右上。

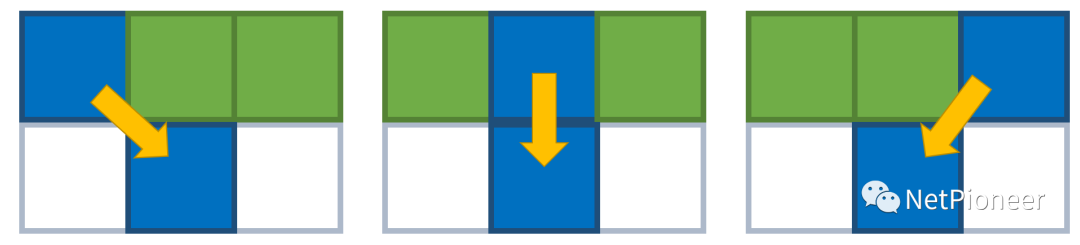
如果我们分别知道它左上、正上和右上的三个像素所在的通路的最低能量，只需要选出能量最低的一条并加上自己的能量，就构成了当前像素的最短能量通路。换言之，这其实是一种归纳法：

·第一行每个像素的累积能量是自己的能量值

·除此之外每一行每个像素的累计能量是上一行的三个相邻像素中最低的累积能量加上自己的能量值

·最后一行的累计能量最低的就代表了一条能量最短的通路

当然，这里还有一个小小的扩展：现在有一个希望缩减的图像，其宽高分别需要缩减 dw 和 dh 个像素。这就意味着这张图象需要删去 dw 和 dh 条能量最小的自上而下的通路和自左而右的通路。我们可以选择先删除自左而右的通路，再删除自上而下的通路，反之亦可。但是为了追求删除通路的总能量和最小——这样全部删除掉的像素对重要物体的影响最小，我们还可以优化这个删除顺序。

这个问题也可以用动态规划的方法解决。不妨记 dq[i] [j] 为原图像在水平缩减 i 个像素长度、垂直缩减 j 个像素长度的过程中所有删去的像素通路的能量值和的最小值，由于宽高分别为 x 和 y 的图像在这种缩放方式下只有可能通过 宽高为 (x+1,y) 或 (x,y+1) 的图像缩减而来，所以有

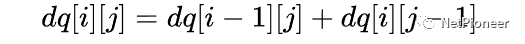
有了上面的经验，读者能否自己理解这个转移方程的含义呢？

最后再来看一个利用Seam Carving方法处理的例子：

|  原图像

|  缩减后

很多细节得到了保留，比起直接拉伸来说要好太多了。

04

结语

本文介绍的这种Seam Carving方法由Avidan等人发明，并发表在2007年的Siggraph中，目前已经有非常广泛的应用，在Photoshop等软件中都可以找到它的身影。比起目前主流的神经网络方法来说，它要简单的多，并且有很大的改良余地，最终效果也不遑多让。有兴趣的同学也可以进一步的研究或者和我讨论。

审核编辑 ：李倩