在重力作用下两个固定点之间悬挂的小链条是什么形状

在重力作用下，两个固定点之间悬挂的小链条是什么形状？这就是经典的悬链线问题，在我们生活中也非常常见，比如两根电线杆之间的电缆。

牛顿力学

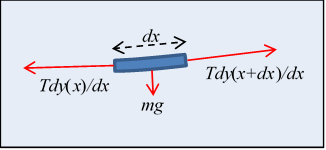
解决这个问题的常规方法是进行受力分析。如上图所示，线的每一点都处于静力平衡状态，并且假设线的单位长度质量为λ，所以mg=λgdx。用曲线y(x)来表示线的形状，由力的平衡我们可以得到以下方程：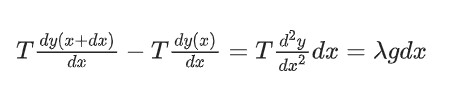

解上面这个微分方程，我们可以得到y=(λg/2T)x²。当然，这是以线的最低点为原点，所以几个积分常数为零。所以，线的形状是一条抛物线。

事实上，在上面的分析中有隐藏的近似值。首先，从x到x+dx之间的线的长度实际是ds，而不是dx。其次，上述分析假设线的张力没有变化，对于几乎接近水平的线来说是一个很好的近似。

但实际上，线的张力随着绳子的高度增加。接下来，我们就实际情况进行分析。

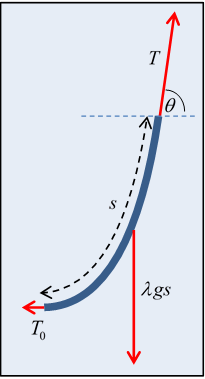
如上图所示，线的底部张力为T₀，在距离底部s处的张力为T，并且与水平方向夹角为θ。那么水平方向力的平衡方程为：Tcosθ=T₀，竖直方向力的平衡为：Tsinθ=λgs，于是就有tanθ=λgs/T₀=s/a，其中a=T₀/λgs为一常数，与具体情况有关。

现在，我们已经有了悬链线的方程，只不过是用θ和s表示，但我们想要的是用水平位置x和竖直位置y表示。我们已经有了斜率dy/dx=tanθ=s/a，并且还有无穷小量之间的关系：dx²+dy²=ds²。把这两个方程放在一起，就可以得到：

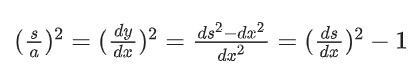
重新排列一下就可以得到：

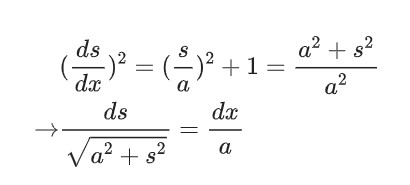
我们令s=asinhξ，则ds=acoshξdξ，代入上式就可以得到dξ=dx/a，两边积分就得到ξ=x/a+b，其中b是积分常数。因此，s=asinh(x/a+b)。在上面我们得到dy/dx=s/a，所以ady=sdx=asinh(x/a+b)dx，最后积分得到悬链线方程y=acosh(x/a+b)+c，其中c是积分常数。两个常数b和c可以根据坐标轴的选取进行确定。

拉格朗日力学        

在以前的文章中，我们用最小作用量原理推导了广义相对论中的测地线方程、量子场论中的基本方程，今天我们继续用它来求悬链线方程。首先，悬链线处于静止状态没有动能，所以我们要求的就是势能的最小值。

审核编辑：刘清