基于直线空间变换的线结构光光平面标定方法

线结构光非接触式测量技术因测量精度高得到了广泛的应用,而其光平面标定结果会直接影响系统的测量精度。为了得到较高的标定精度,很多专家学者对此进行了研究。现在主要的标定方法有基于平面靶标法、基于平面直线拟合及直线消影原理法,其中关于平面靶标法的研究较为广泛。

研究团队提出了一种基于直线空间变换的线结构光光平面标定方法。该方法根据平面单应性矩阵快速求解靶标面的二维直线方程,并根据靶标坐标系的特殊性构建三维Plücker矩阵形式直线方程,利用直线进行光平面拟合;充分利用整条激光线数据,不需要求解靶标面方程和投影面方程,另外采用直线进行拟合时,利用滑动平均法和正交回归拟合法,保证了前期数据点的抗噪性,增加了标定结果的准确性,从而所提方法满足实际线结构光的测量要求。

一、线结构光视觉测量模型

线结构光测量装置主要由激光投射器和相机组成,其几何结构如下图所示。OwXwYwZw为世界坐标系, OcXcYcZc为相机坐标系, ouv为图像坐标系,点 P为激光线与待测物体交线上任意一点,其在图像平面上对应的投影为点 p。

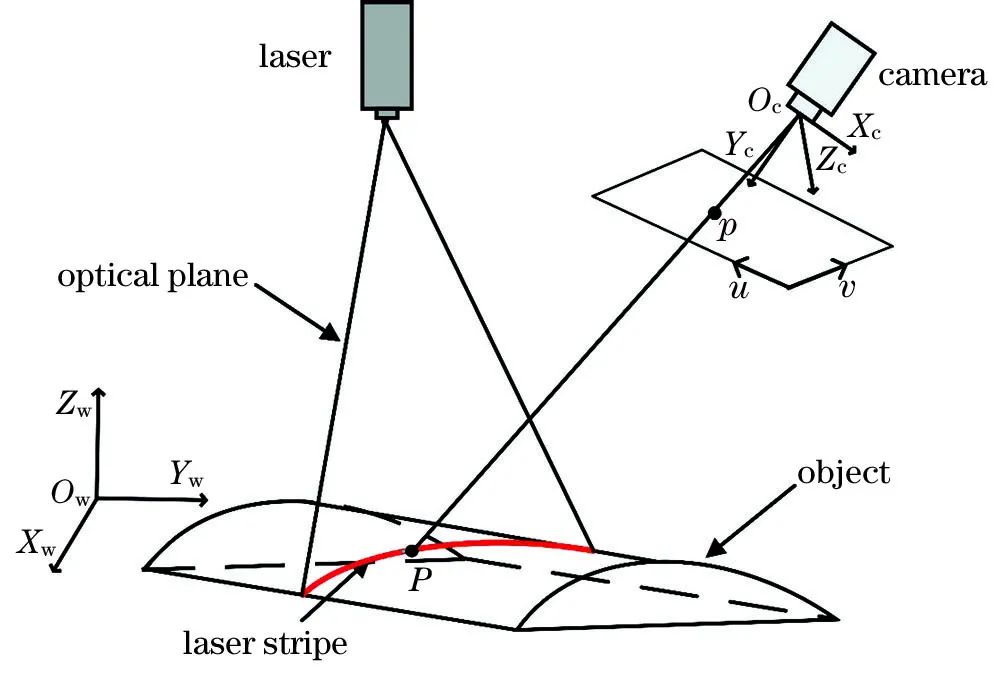
根据建立的相机成像透视模型,图像坐标系下的点 (u,v)经相机射影变换后与世界坐标系下的点 (xw,yw,zw)的对应关系为

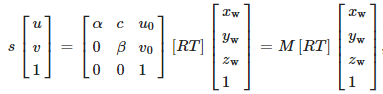
相机坐标系下,线结构光的光平面方程可表示为：

A⋅xc+B⋅yc+C⋅zc+D=0

二、基于直线空间变换的光平面标定方法

2.1 平面光条中心线提取

实际生产环境中,光条成像受外界光源、靶标面不均匀反射影响,存在很多噪声,它们会影响光条中心的提取。采用互相关算法,利用邻域光条纹的相关联性提取光条,即在场景本身深度与物体表面反射特性未发生突变的场合下,条纹灰度的变化是相对平稳的。因此,相邻条纹中心点间的坐标位置与灰度值均具有一定的相似性,利用这种相似性可以在很大的程度上降低噪声的干扰,从而能够提高中心条纹提取精度。以行为单位,使用灰度重心法提取光条中心。另外在光条作用于平面成像为一条直线的前提下,利用五点滑动平均(5MA)法对提取的光条中心点进行预处理,实现过程如下图所示。

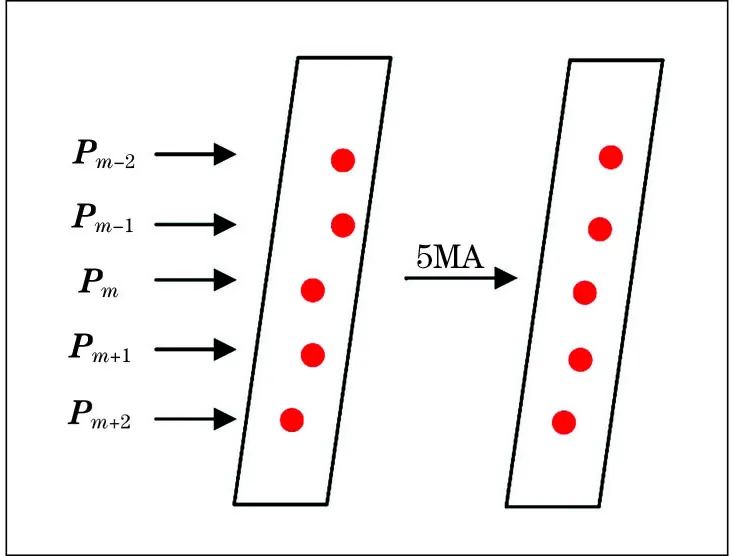
5MA法取邻近5点均值来消除光条点的随机误差,即由当前点 p=(xm,ym)与上下临近4个点的平均值确定 p'=(x'm,y'm),公式为：

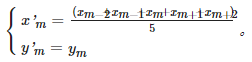
直线拟合常用方法有代数距离和欧氏距离2种。代数距离只考虑光条点集 y与观察值 y˙之间的距离约束,忽略了 x方向的误差,且无法表示竖直方向的直线,据文献,正交回归法具有较好的拟合效果与旋转不变性。为此采用点法式正交回归法拟合光条中心线,以点到直线的欧氏距离建立新约束函数 e:

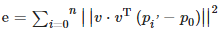
2.2 空间直线方程求解

在二维射影变换中,平面直线方程 a⋅u+b⋅v+c=0的齐次表达式为：

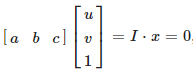
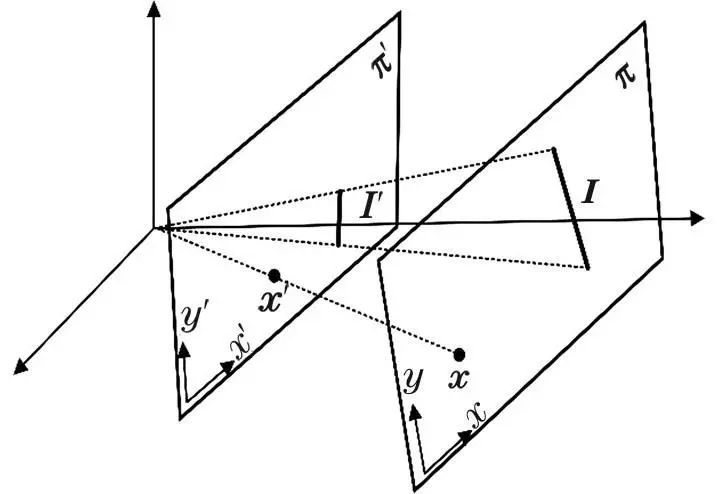
满足中心投影映射的两个平面之间存在单应性矩阵 H变换关系,如图3所示,两平面中对应点 x'与 x满足的对应关系为：

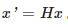
利用图像上光条中心点与靶标面上点之间的单应性关系和直线方程的齐次表达式,可推导得到两平面上光条中心线单应性变换关系为：

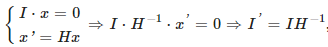
如图4所示,在建立的空间直线变换模型中,靶标面上所有点具有特殊性,其在靶标空间坐标系中满足zw=0,为此可将原先的二维直线方程上的点全部拓展至三维。选取光条上任意两点 A=(xa,ya,za,1)T,B=(xb,yb,zb,1)T,其中za=zb=0,将空间直线的方程组解析式转换成Plücker矩阵形式,便于矩阵运算,直线的Plücker表达形式 Lw不受取点大小影响。Lw的表达式为：

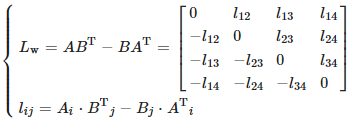
靶标与相机坐标系的转换关系可用相机成像模型(8)式求解得到:

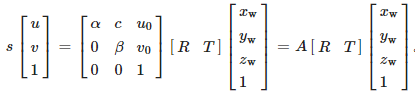
图像上圆形标记点与靶标坐标系下的圆形标记点之间存在N点透视关系PnP(perspective N-point),因此可建立两者之间的重投影误差函数,使用Levenberg-Marquardt算法优化重投影误差函数,获得非线性最优解 R和 T。根据坐标系转换,得到了两坐标系下对应点的关系,表达式为：

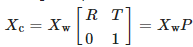
进一步可推出空间直线变换对应关系为：

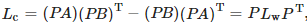
2.3 光平面方程计算

激光线 Lc为光平面 π与靶标平面交线,其与光平面共面,根据线面约束方程,可知：

Lc⋅π=0

多次移动靶标平面( n≥2),得到多组光平面上的直线 Lci,建立线面方程组：

LT⋅π=0,L=(Lc1,Lc2,…,Lcn)

由于参与拟合光条直线方程的数据存在提取误差,可增加激光线数量,将多个线面约束方程求解问题转换成超静定齐次方程组的最小二乘解问题,利用SVD分解 L(L=UDVT),其中 U为酉矩阵, D为奇异值沿对角线从大到小构成的对角矩阵, V为酉矩阵。D中最小奇异值在 VT对应的特征向量为平面方程的系数 π,从而完成光平面方程参数求解。

三、试验结果

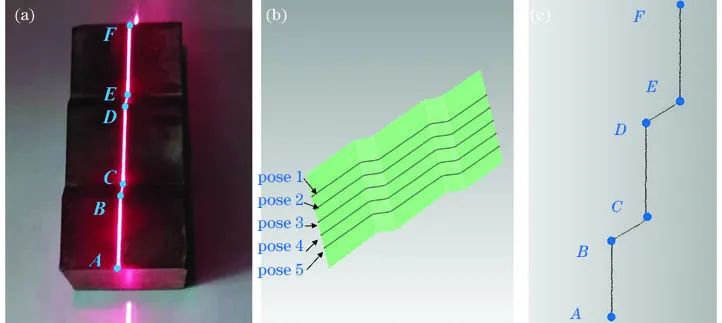
标准台阶块实验。(a)台阶块及特征点;(b)台阶点云;(c)截面形状

圆柱实验。(a)圆柱样件;(b)拟合圆

作者：翟鹏, 崔海华, 胡广露, 张益华, 靳宇婷, 黄怡.

       审核编辑：郭婷