如何实现PCB板边倒圆角

jf_iZR6mdqV 2022-11-14 5725

PCB设计

2541人已加入

描述

当PCB外形是直角时,通常工程制作外形(锣带）时,会将直角或尖角的地方倒成圆角，主要是为了防止PCB容易划伤板他扎伤人。

所以当客户没有特殊要求时,PCB外形是直角一般会默认倒角0.5mm圆角(如下图所示)

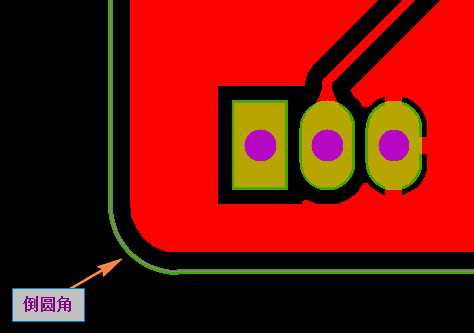
一、PCB板边倒圆角点分析

原PCB外形如下图图示:看了这个PCB外形,产生有2个问题点：

1.外形中哪些点需倒圆角?

2.如何怎么倒圆角?

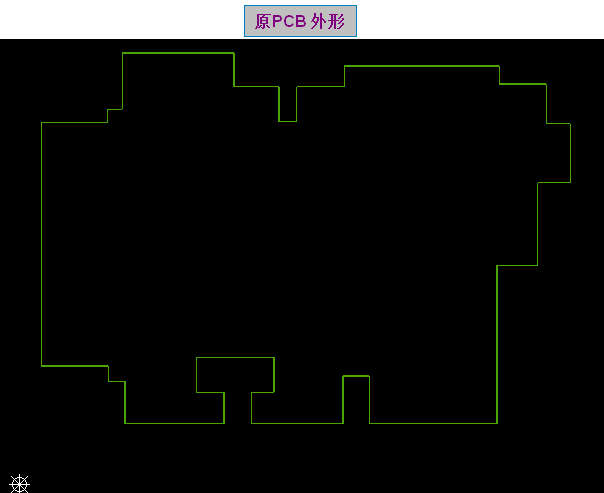
1.外形中哪些点需倒圆角?

看下图: PCB外形倒圆角的点,刚好就是我们凸包需求出的点,接下来我们将玩转凸包了,只要求出凸包，那么就可以实现PCB板边倒圆角啦。

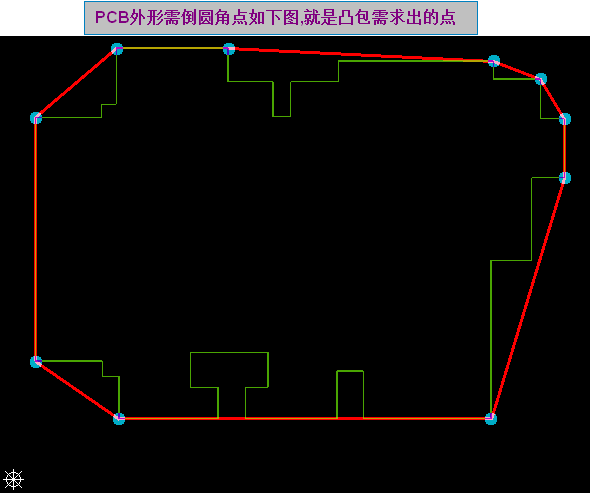
求凸包的算法：我们可以借鉴算法导论中的查找凸包的算法（加以改进得到新的求凸包方法，详见【方法一】与【方法二】）

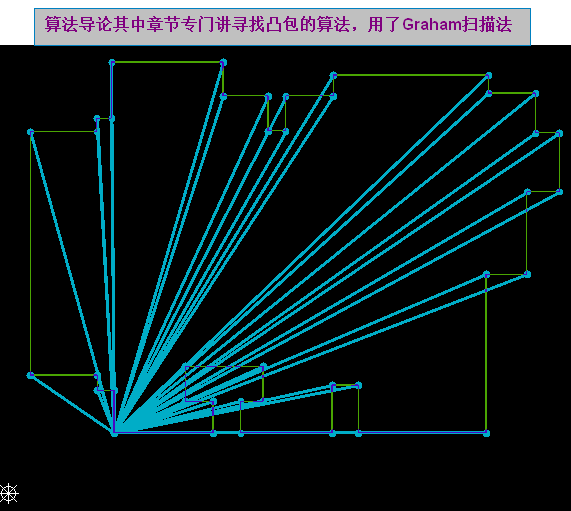
2.如何倒圆角?

在下面有说明倒角方法.

二、求凸点

方法一求凸点：【采用多轮遍历,一遍一遍将凹点踢除，剩于的即是凸点】

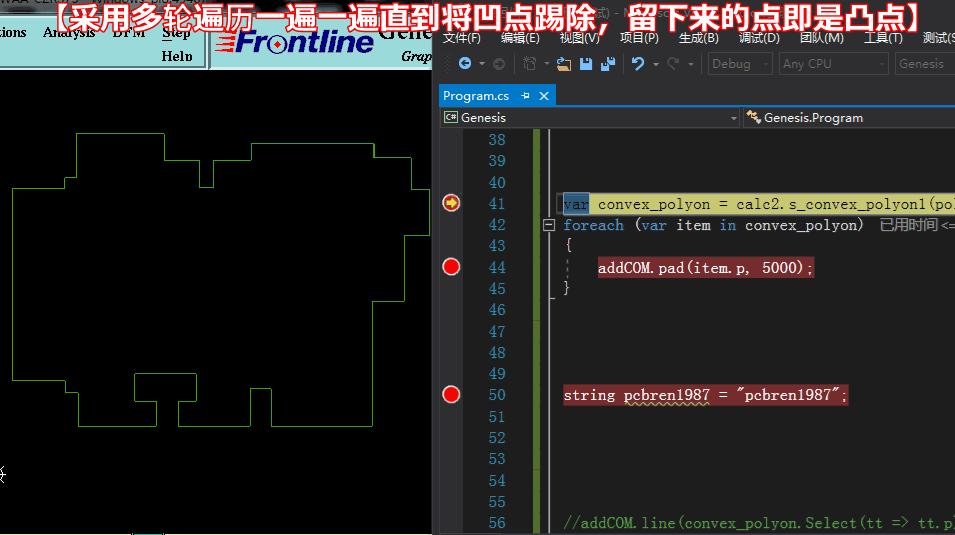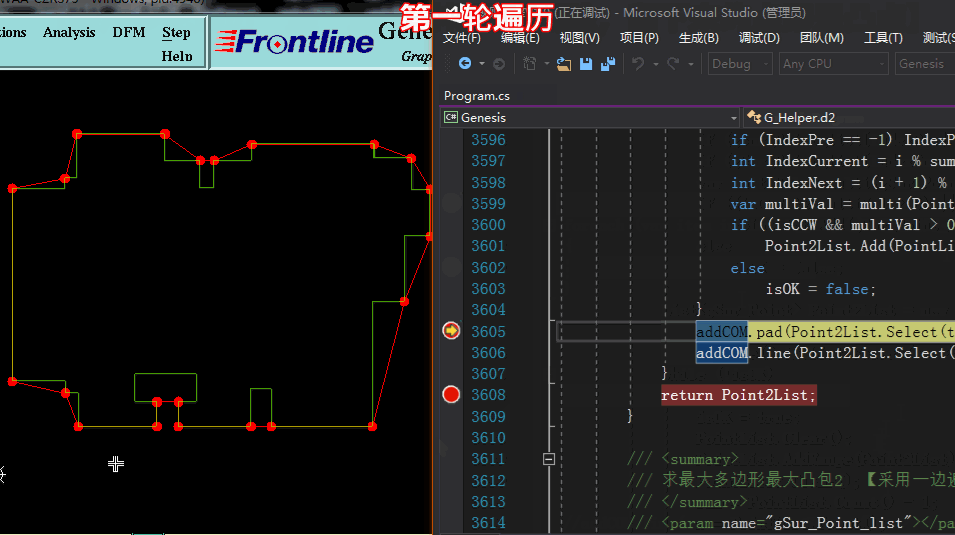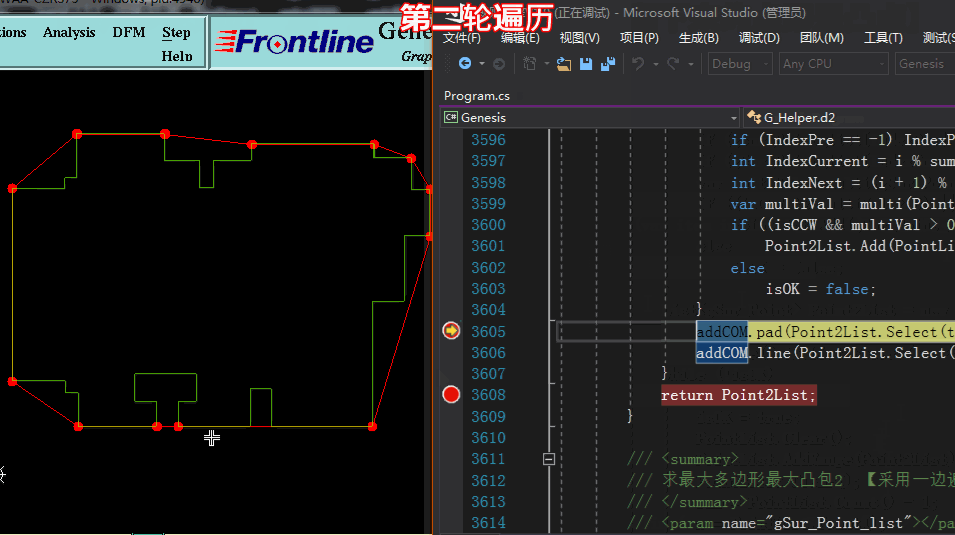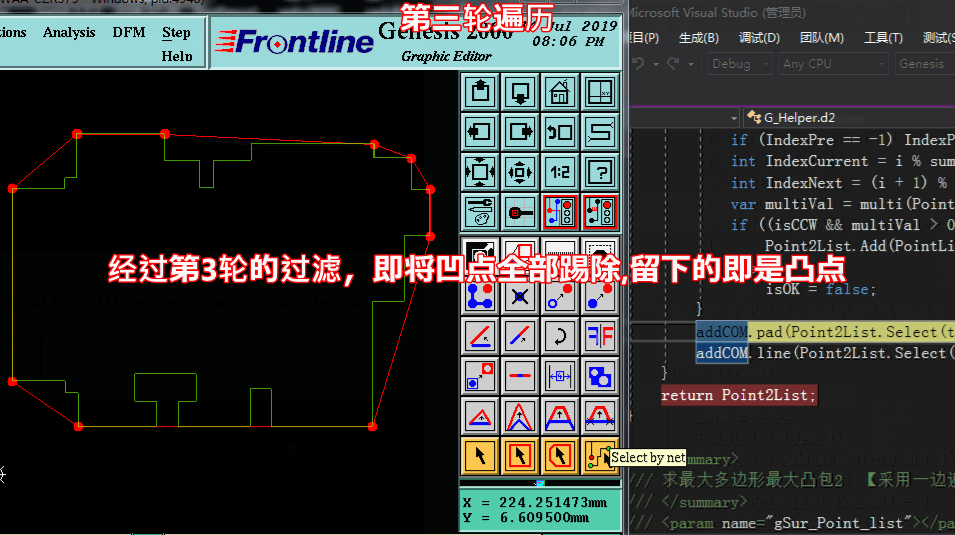
方法一求凸点: 代码

///

/// 求最大多边形最大凸包1 【采用多轮遍历将凹点踢除，剩于的即是凸点】
///

///
///
public List s_convex_polyon1(List gSur_Point_list) {
add addCOM = new add();
bool isOK = true;
List PointList = new List();
var isCCW = s_isCCW(gSur_Point_list);
int sum = gSur_Point_list.Count() - 1;
int n = gSur_Point_list.Count();
for (int i = 0; i < n; i++) {
int IndexPre = (i - 1) % sum;
if (IndexPre == -1) IndexPre = sum - 1;
int IndexCurrent = i % sum;

int IndexNext = (i + 1) % sum;
if (gSur_Point_list[IndexPre].type_point > 0) continue;
if (gSur_Point_list[IndexCurrent].type_point > 0) continue;
var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
PointList.Add(gSur_Point_list[IndexCurrent]);
else isOK = false; }
List Point2List = new List(PointList);
while (!isOK) {
isOK = true;
PointList.Clear();
PointList.AddRange(Point2List);
Point2List.Clear();
sum = PointList.Count() - 1;
n = PointList.Count();
for (int i = 0; i < n; i++) {
int IndexPre = (i - 1) % sum;
if (IndexPre == -1) IndexPre = sum - 1;
int IndexCurrent = i % sum;
int IndexNext = (i + 1) % sum;
var multiVal = multi(PointList[IndexPre].p, PointList[IndexCurrent].p, PointList[IndexNext].p);
if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
Point2List.Add(PointList[IndexCurrent]);
else
isOK = false;
} }
return Point2List; }

方法二求凸包：【采用一边遍历找出凸点并加入队列，并同时将队列中的凸点队列中找出凹点踢除】

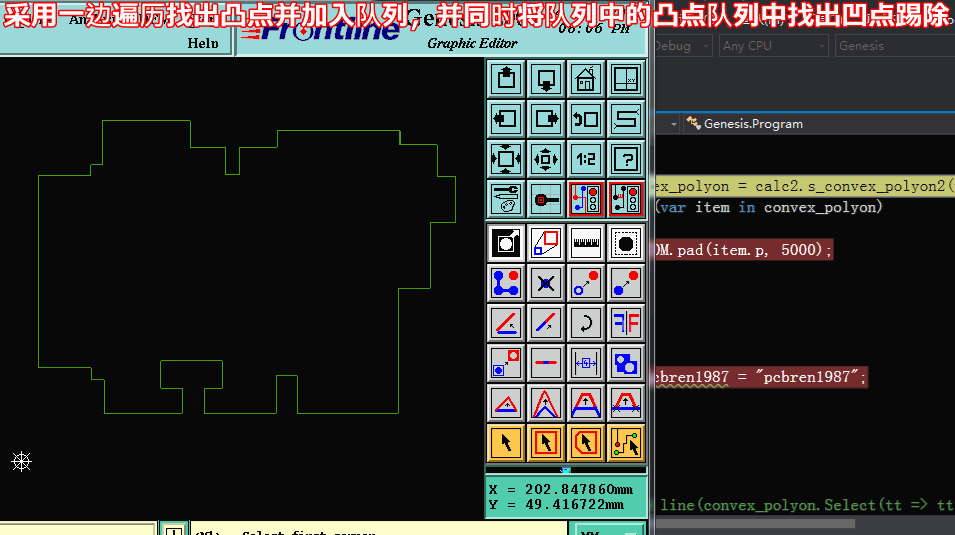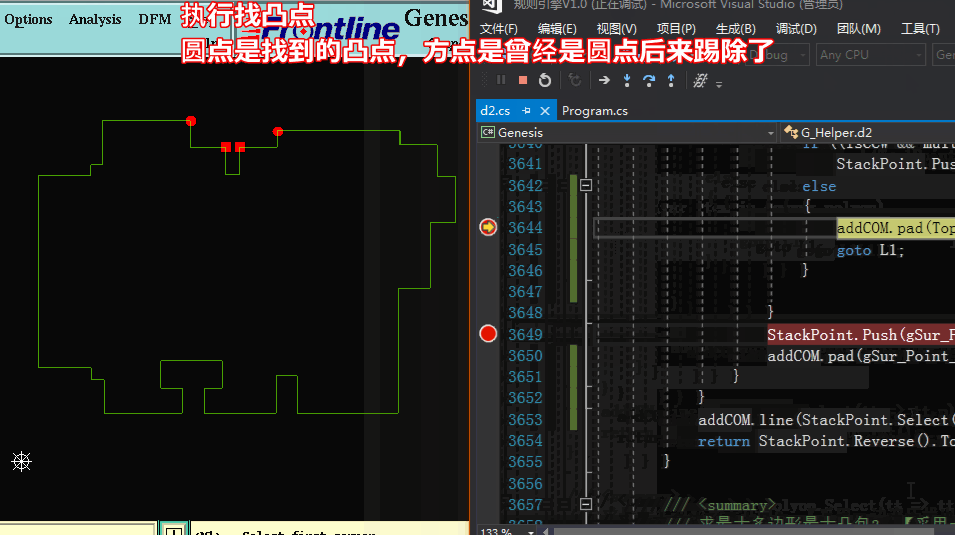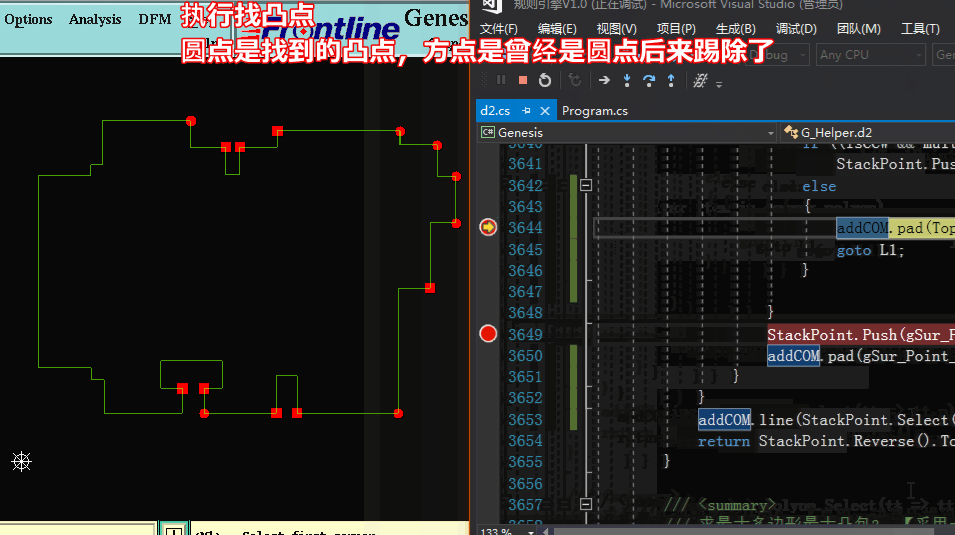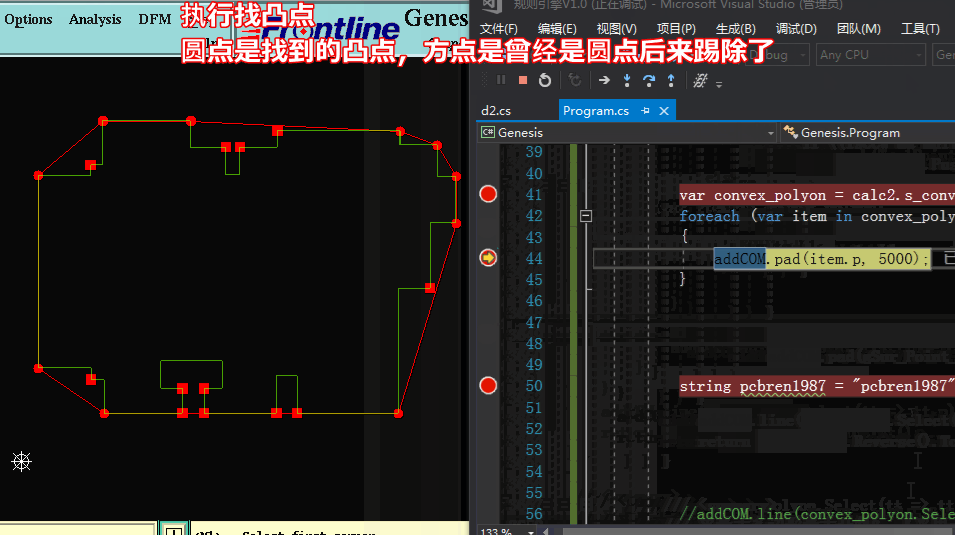
方法二求凸包：代码

///

/// 求最大多边形最大凸包2 【采用一边遍历找出凸点并加入队列，并同时将队列中的凸点队列中找出凹点踢除】
///

///
///
public List s_convex_polyon2(List gSur_Point_list) {
Stack StackPoint = new Stack();
var isCCW = s_isCCW(gSur_Point_list);
int sum = gSur_Point_list.Count() - 1;
int n = gSur_Point_list.Count();
for (int i = 0; i < n; i++) {
int IndexPre = (i - 1) % sum;
if (IndexPre == -1) IndexPre = sum - 1;
int IndexCurrent = i % sum;
int IndexNext = (i + 1) % sum;
if (gSur_Point_list[IndexPre].type_point > 0) continue;
if (gSur_Point_list[IndexCurrent].type_point > 0) continue;
var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0)) {
L1:
if (StackPoint.Count > 1) {
var Top1Point = StackPoint.Pop();
var Top2Point = StackPoint.Peek();
multiVal = multi(Top2Point.p, Top1Point.p, gSur_Point_list[IndexCurrent].p);
if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
StackPoint.Push(Top1Point);
else goto L1;
} StackPoint.Push(gSur_Point_list[IndexCurrent]);
} }
return StackPoint.Reverse().ToList(); }

方法三求凸包：【按算法导论Graham扫描法各节点按方位角+距离逆时针排序依次检查,当不属凸点于则弹出】

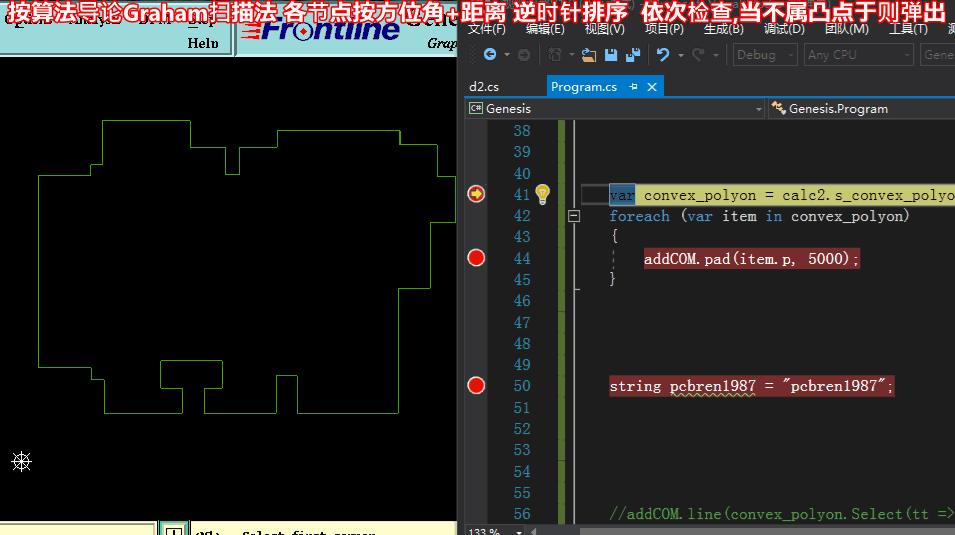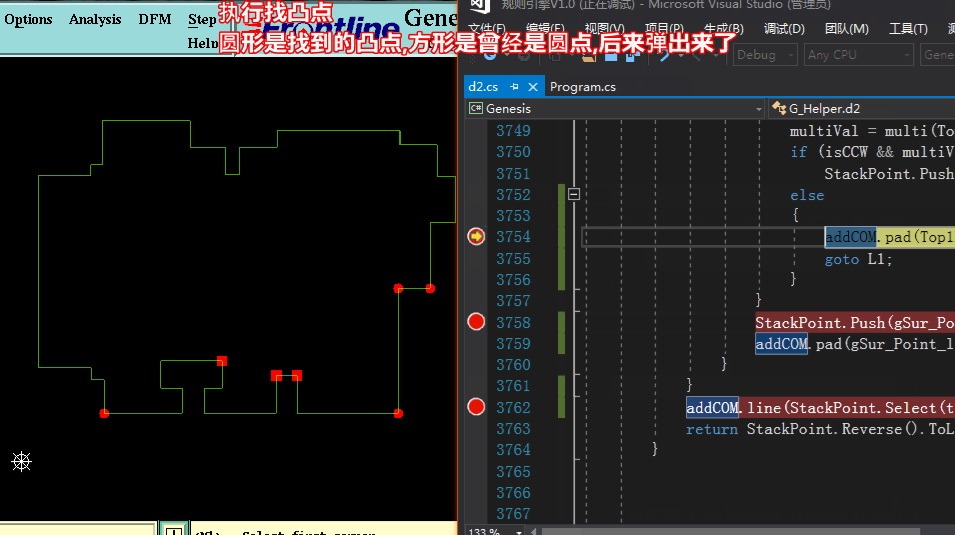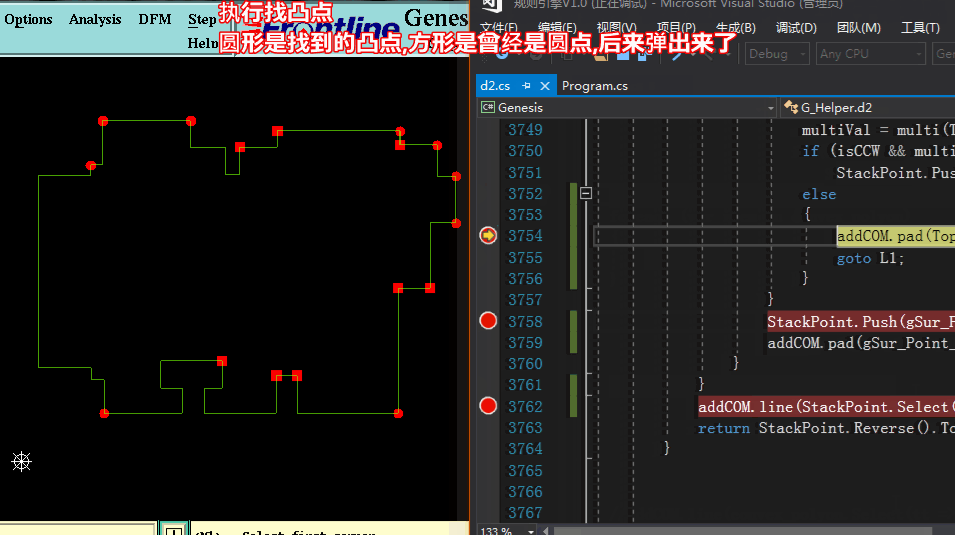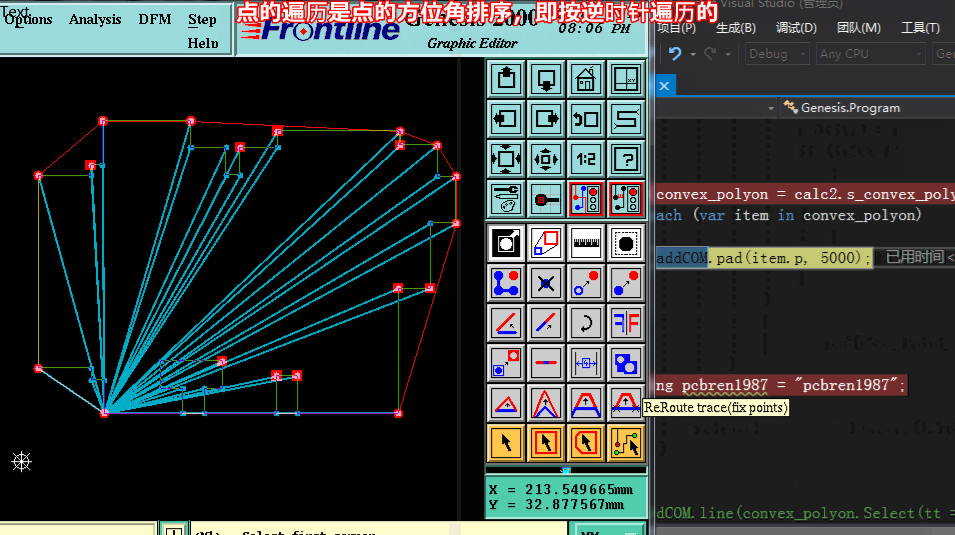
方法三求凸包：代码

///

/// 求最大多边形最大凸包5 【按算法导论Graham扫描法各节点按方位角+距离逆时针排序依次检查,当不属凸点于则弹出】 /// 由于把各点的排列顺序重新排序了，只支持折线节点(当存在弧节点时会出异常！！！) ///

/// ///
public List s_convex_polyon3(List gSur_Point_list)
{ var LeftBottomPoint = gSur_Point_list.OrderBy(tt => tt.p.y).ThenBy(tt => tt.p.x).FirstOrDefault();
gSur_Point_list.RemoveAt(gSur_Point_list.Count - 1);
gSur_Point_list.ForEach(tt =>
{
tt.Value = p2p_di(LeftBottomPoint.p, tt.p);
tt.Angle = p_ang(LeftBottomPoint.p, tt.p);

} ); gSur_Point_list = gSur_Point_list.OrderBy(tt => tt.Angle).ThenBy(tt => tt.Value).ToList();
gSur_Point_list.Add(gSur_Point_list[0]);
Stack StackPoint = new Stack();
var isCCW = true;
int sum = gSur_Point_list.Count() - 1;
int n = gSur_Point_list.Count(); for (int i = 0; i < n; i++)
{ int IndexPre = (i - 1) % sum;
if (IndexPre == -1) IndexPre = sum - 1;
int IndexCurrent = i % sum; int IndexNext = (i + 1) % sum;
var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
if (isCCW && multiVal > 0) {
L1:
if (StackPoint.Count > 1)
{ var Top1Point = StackPoint.Pop();
var Top2Point = StackPoint.Peek();
multiVal = multi(Top2Point.p, Top1Point.p, gSur_Point_list[IndexCurrent].p);
if (isCCW && multiVal > 0) StackPoint.Push(Top1Point);
else goto L1;
}
StackPoint.Push(gSur_Point_list[IndexCurrent]);
} } return StackPoint.Reverse().ToList(); }

公共方法与数据结构

View Code

三、板边凸点倒圆角方法

方法一：也最简单的倒角方法,我们将PCB板边凸点找出来后，可以直接借助genesis倒角功能就可以实现了

当然但偶尔会报错的, 且当N个小线段组成的尖角倒角会出错(要实现完美效果只有自己写倒角算法啦)

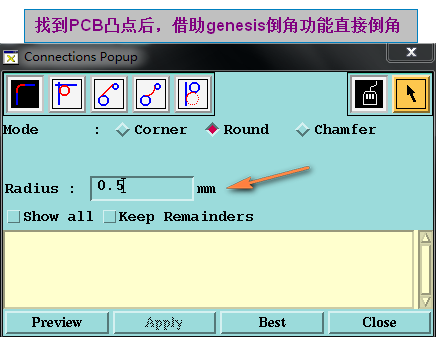
方法二：自己写倒角算法，这个算法和加内角孔算法类似（这里只是介绍简单的倒角)考虑特殊的需要扩展

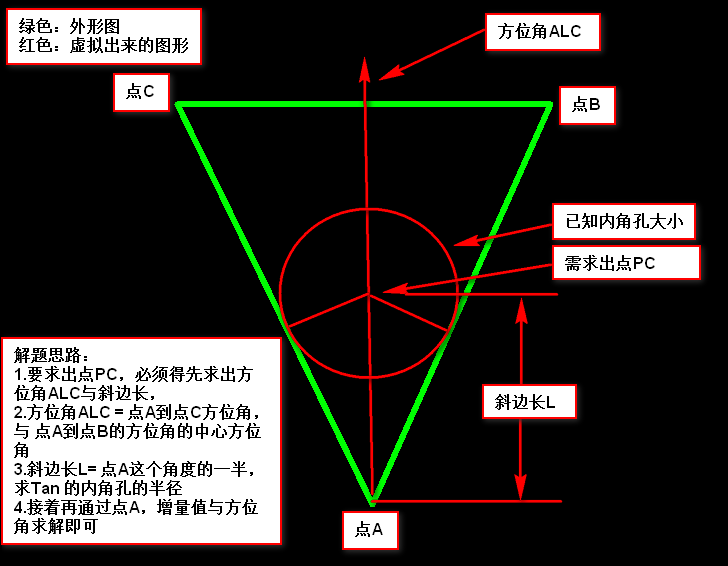
四、凸点加倒圆角实现效果

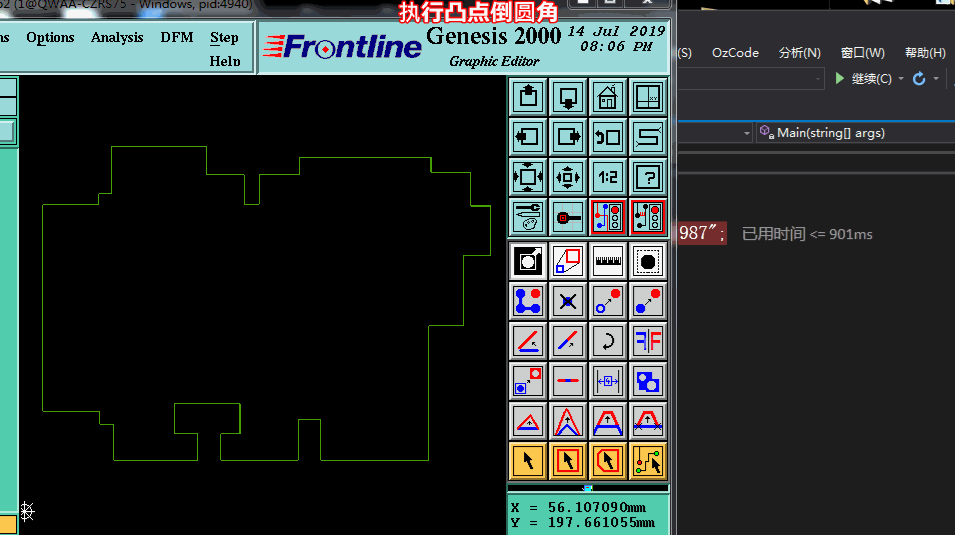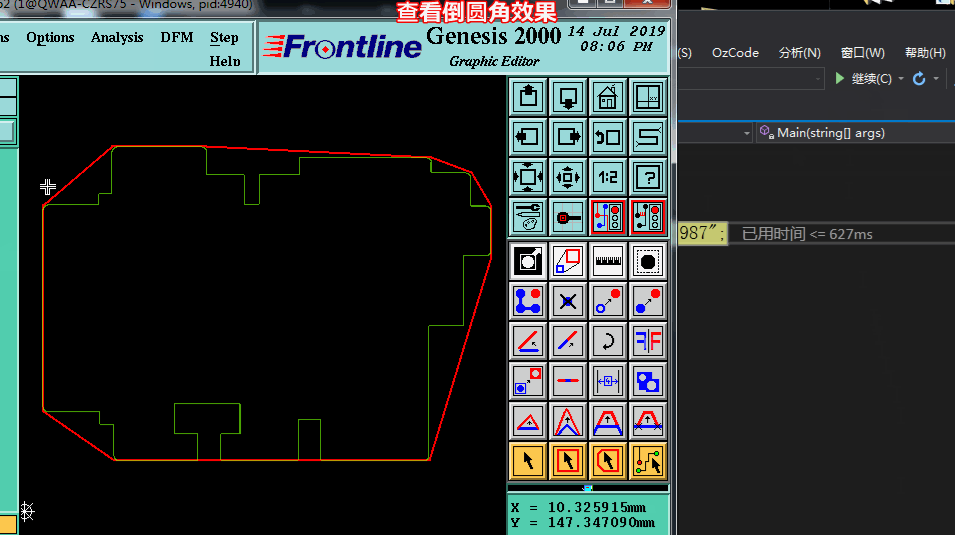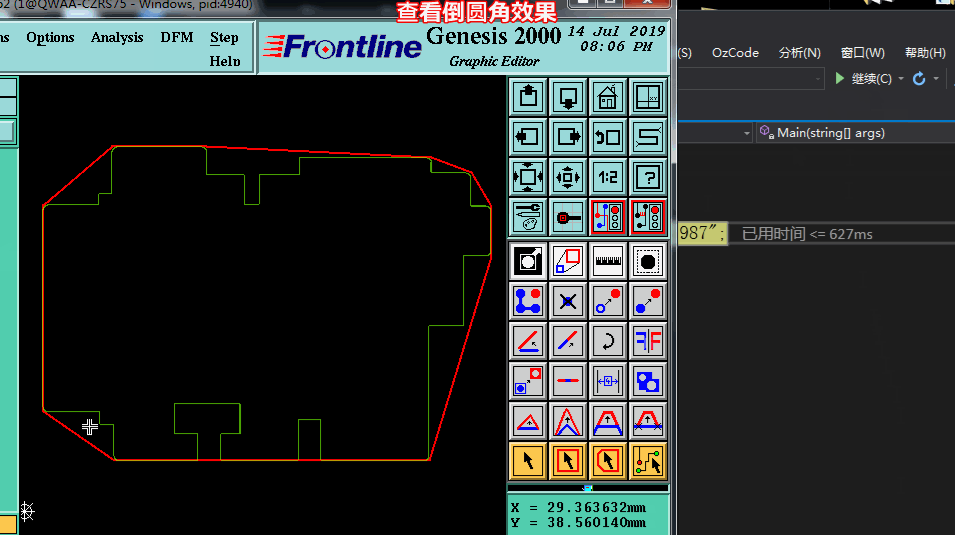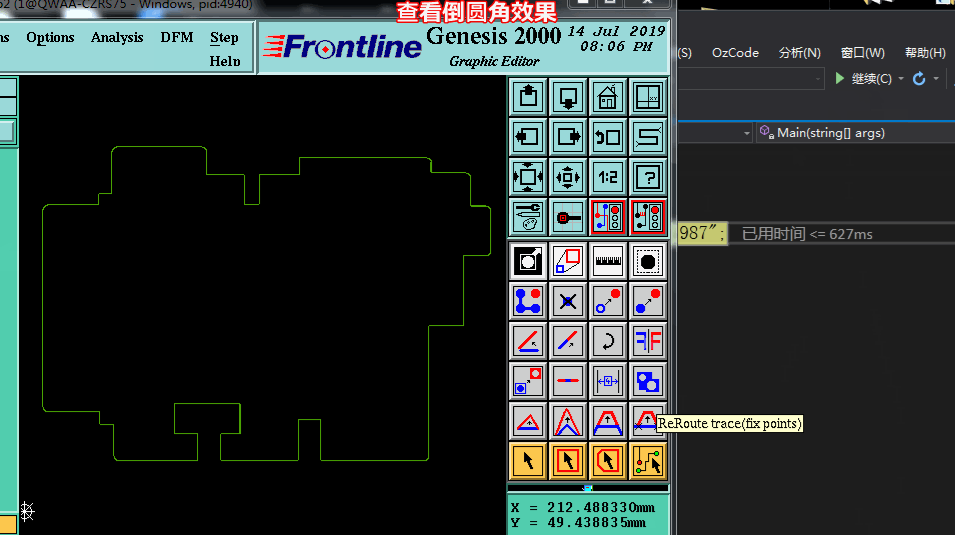
编辑：黄飞

打开APP阅读更多精彩内容