

PCB上的串扰的三种产生机制
PCB设计
描述
PCB上的串扰的产生机制,可以认为有三种:电感耦合,电容耦合还有共阻耦合(common-impedance coupling)。
电感/电容耦合
假设两条微带线,中心到中心的距离为d,如下图所示。
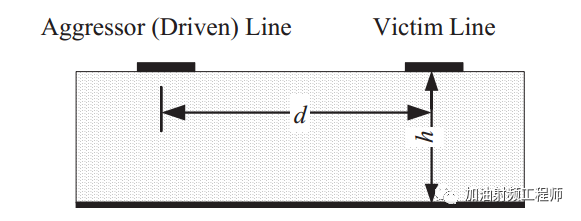
当信号沿着传输线传播时,微带线周围开始有电场线和磁场线。
但是,这些电场线和磁场线并不是只在信号和它相关的回路中,而是会延伸到周围区域。如下图所示。
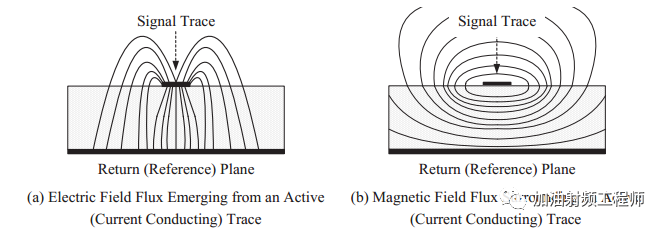
从传输线发出的电场终止与任何相邻的金属结构;传输线周围的磁场也会部分环绕在任何相邻的金属结构周围。
那如果相邻的金属结构恰好是一根信号传输线呢?
则该根传输线会由于接收到的施扰微带线产生的电磁场,而产生相应的电流和电压。
很显然,如果两条传输线之间的间隔增加,信号传输线接收到的场会迅速下降。
但是,如果它们足够近,则相邻信号传输线则会上产生的干扰电流。而这些干扰电流,和传输线上本来的信号电流一样,也会经历反射、失真和辐射。
也就是说,如果有个很脏的微带线A,它旁边有个很干净的微带线B,则B就会被A弄脏,而且如果B正好靠近输出端,则B就会把从A耦合过来的噪声辐射出去。
微带线之间的电场和磁场耦合,分别被称为电容和电感耦合。
电容耦合和电感耦合,它们各自对串扰的影响很大程度上取决于电路布局。
下图所示,是串扰的简化模型,包含了PCB上传输线之间的电容和电感耦合。
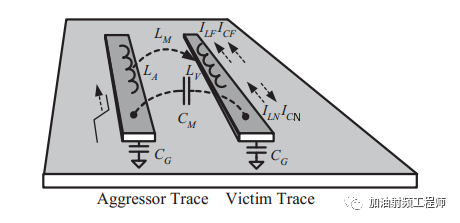
CG,存在于微带线和参考平面之间,会影响微带线的特性阻抗和信号传播延迟。
CM, 存在于微带线之间,是不希望的电容耦合。
LA和LV分别代表施扰和受扰微带线的自感,会影响微带线的特性阻抗和信号传播延迟。
LM,代表两跟微带线之间的互感 LM ,会导致两个电路之间的电感耦合。
在电小尺寸的微带线中,电容耦合表现为与受扰线并联的电流源,电感耦合表现为与受扰线串联的电压源。
具体关系,如下列式子所示:
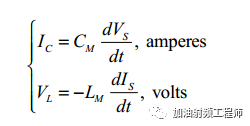
其中,IC和VL分别是受扰微带线中的电容感应电流和电感感应电压,这是由于施扰微带线中的源电压 VS 和电流 IS 的变化而引起的。
实际情况中,电容和电感串扰机制同时存在。
电容耦合,在受扰微带线上产生的电容感应电流会向两端传播,即分别向前传播、朝向远端ICF,和向后传播、朝向近端ICN。
电感耦合,在受扰微带线上产生的电感感应电压,在受扰微带线上产生电流(ILF,ILN),其方向与IS相反。(参考文献中,IILF,ILN的方向可能标注错了,这里改了一下,上图红色标注)
因此,电容耦合和电感耦合信号在向后传播时,电流叠加,耦合增强;在前向传播时,电流趋于抵消。
向后流动的总耦合信号称为“反向串扰”或“近端串扰”(NEXT),而向前流动(实际上抵消)的总耦合信号称为“前向串扰”或“远端串扰” ”(FEXT)。
近端串扰和远端串扰的特征显着不同:近端串扰是一个恒定幅度的脉冲,其脉冲宽度为走线之间耦合区域传播时间的两倍,而远端串扰的特点是窄脉冲,其宽度等于干扰信号的transition time,信号度随着走线之间的耦合区域的增加而增加。
那怎样减少电感和电容耦合呢?
答案就是,减小微带线和参考平面的距离。
微带线与参考平面之间距离减小,CG增加,电容耦合显著减小。
微带线与参考平面之间距离减小,参考平面成为首选返回路径,电感耦合也大大减少。
在数字电路中,由于数字驱动器的低阻抗特性,电感耦合比电容耦合更占主导地位,而电容耦合在高阻抗(通常是模拟)电路中更占主导地位。
共阻抗耦合
PCB 中的第三种也是非常重要的耦合机制是共阻抗耦合。
施扰微带线的回流路径和受扰微带线的回流路径公用一部分,从而产生共阻抗耦合。
当嘈杂的大电流(例如数字)电路与敏感(例如模拟)电路共享公共返回路径时,结果就是,歇菜。
高频信号的回流,大部分存在于微带线下方的参考平面上,但是有一小部分,会扩散到两侧。
其在参考平面上的回流密度,可由下式表示:
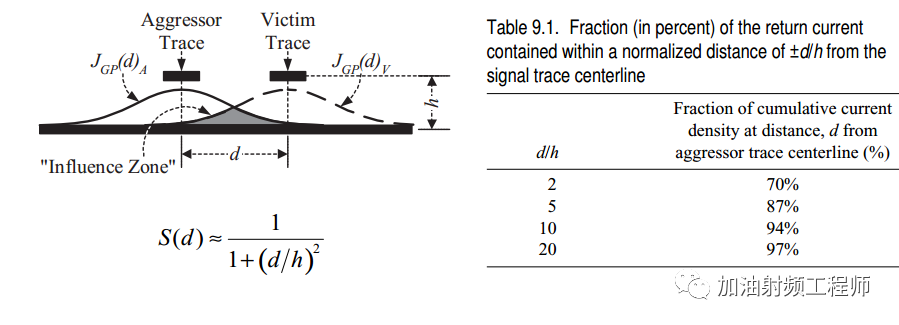
如上图所示,JGP(d)A和JGP(d)V分别是施扰微带线和受扰微带线的电流密度分布。两者交叠的部分,即上图中的灰色部分,即是"影响区域",这部分决定了两根微带线之间的影响程度。
施扰微带线回流的一部分,在受扰回流路径中流动,因此施扰微带线上的噪声就被耦合到受扰微带线中。
举个例子(感觉原文中的数据有点错误,这边按照我的理解改了一下):
假设一个高速大电流的MCU和模拟电路公用一个参考平面。模拟电路中包含一个24 位 A/D 转换器,假设其电源为1V,则其最低有效位相当于为1/2^24=59nV。
假设参考平面的阻抗为40uohm,则59nV对应电流为1.5mA。
假设,MCU需要10A的电流,则1.5mA,相等于10A的数字电流的 0.015%。
为了避免干扰,必须增加数字和模拟迹线之间的必要间隔 d,以便 99.985% 的数字回流包含在距信号迹线中心线的距离内d。
假设高度h为10 mil ,这需要大于 200 mil(或 5 mm)的间距 d。这个宽度,在现代 PCB 设计中几乎不可能实现。
此时,分割参考平面,是一种解决这种矛盾的方法。
参考文献:grounds for grounding
编辑:黄飞
-
什么是串扰?PCB走线串扰详解2023-09-11 2326
-
用于PCB品质验证的时域串扰测量法分析2018-11-27 1672
-
PCB的三种特殊布线技巧2019-05-07 1994
-
PCB设计中串扰的产生以及如何避免2018-01-26 6100
-
高速PCB设计中如何消除串扰?2019-07-25 3970
-
串扰问题产生机理及解决方法2019-08-14 25709
-
如何解决PCB串扰问题2020-07-19 2816
-
浅谈串扰溯源,串扰是怎么产生的2021-03-29 4133
-
串扰的类型,串扰产生的原因?2023-07-06 3386
-
如何减少PCB设计中的串扰问题 PCB串扰的机制和原因2023-07-20 3923
-
pcb上的高速信号需要仿真串扰吗2023-09-05 1436
-
pcb中的串扰机制是什么2024-01-17 1129
-
PCB产生串扰的原因及解决方法2024-01-18 3076
全部0条评论

快来发表一下你的评论吧 !

