物理学中的波概念

01 导论  

地球与其它已知星球之最大区别在于地球的表面上存在大量的水。水是生命发生的前提，自然也是物理学发生的前提。水给物理学打上了深深的特征烙印，波(wave)、涨落(fluctuation)、镜像(mirror image)、涡旋(vortex)等关键物理学概念都来自于水。水表面处的分子密度大于体内，其表面张力在20 ℃时~72.75 mN/m，可以说水有一张弹性适中的皮，极易表现出水面的波动(图1)。因此，水波也就成为了一个人类也许在有文明之前就烂熟于胸的概念。水波随处可见，深入人心，也就深入了物理学！

在物理学中，取决于具体的语境，波被用来表示一种运动的形式，也被当作存在的形式，甚至有时不过只是一个空洞抽象的数学表达式。在机械波、电磁波(光波)、物质波(量子力学波函数)以及引力波这些概念中出现的波，以及在傅里叶分析和信号探测理论与实践中也许是隐性地提及的波，可能多有可检讨的内容。认真分析一下这些波的含义，其所依托概念的来源，其所由来的原初约束与限制，以及其下所依赖的数学，也许可以为对相应的物理学的深刻理解有些许的帮助。

2 机械振动与机械波  

固体经历微小形变时，形变与应力成正比，此即为胡克定律F = -kx ，泰勒展开保证了这个公式的普适性。考察弹簧上一质量为m的振子的振动问题，引入ω2 = k/m ，则振子的运动方程为

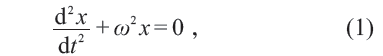
此方程解的形式为

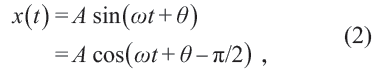
这是一个单变量的三角函数。这即是说，振动在数学上被表示为位置关于时间的三角函数。与此同时，匀速圆周运动可表示为参数方程

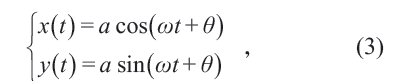
可见匀速转动在任一方向上的投影是(2)式表述的简单振动。这说明，振动和转动实质上有某种一致性。振动与转动之间的转换是工业文明的基础。一个显见的例子是，缝纫机上踏板的来回振动会转化为传动轮的转动，传动轮的转动又转化为缝纫针的上下振动。缝纫针按照(2)式的谐振动(harmonic oscillation)， 配合布料的匀速直线运动，会留下周期性的针脚。

如果振动的物体有足够的外延，比如一根弦，其上各点的振动之间则可能会是以某种方式耦合的。一根取向沿x 方向的弦的运动方程，在小振幅近似下，为

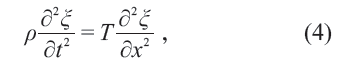
其中ρ 是弦的质量密度，T 是弦(因沿x 方向被紧绷引起)的张力， x ∈[0，L] ，L 是弦长。方程(4)可改写为

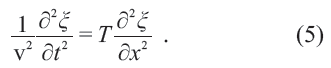
方程(5)形式的关于时间—空间变量的二阶微分方程是所谓的经典波动方程。注意，空间变量可以多维的。对于一维情形，方程(5)的通解为

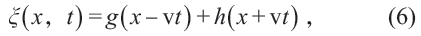
人们把其中形式如

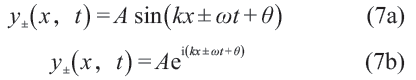
的称为行波解，其中的k，ω，满足v = ω/k ，反映的是振动的长度周期和时间周期(一维情形下，k，ω就是两个数)。注意，弦上的每一点都在与弦垂直的平面内某个方向上振动，所谓的波速v反映的是点振动之间的关联。实际上，人们也愿意把k，ω看作是实在的物理量，ω是频率，k 是波矢。波矢，表征波传播的方向，但实际上它是个切空间里的概念。在三维空间中定义的形如ξ(x，t) = Aei(k ⋅ x - ωt + θ) 的函数，被称为平面波，意思是波前(wave front)为与方向x垂直的整个平面。平面波展开是常用的计算方法，其合理性和有效性基于傅里叶分析。

(5)式的波动方程和类似(7)式中的表示波的函数，都被当作经典物理中谈论波的基础，甚至成了波的化身，但其实它们远远不足以反映机械波的复杂性。比如，1834 年英国人John Scott Russell发现水渠中行驶的船头总有一个高高的浪头。此现象涉及的浅水波概念被称为孤立波。此情景中，水面的运动满足KdV 方程

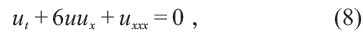
其解的形式为

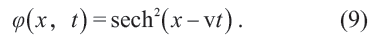
此解与(7)式中的解有相同的本质，是x - vt 形式的变量的三角函数(双曲函数是虚变量的三角函数)。这反映的是人们数学水平的局限，而非自然现象必然严格如此。

3 光的波动说  

光充满宇宙。牛顿认为光是由颗粒(corpuscle)组成的，笔者猜测这可能是来自同雨丝的类比。光线与雨丝一起从夏日的乌云处一起落下，都给人以ray(射线)的印象。雨丝里有一个个的小雨滴，那光线也可能是由分立的颗粒组成的，只是颗粒个头太小不易分辨而已。荷兰的惠更斯比较水波的形象和烛光摇曳的影子，认为光应该是水波那样的波，此为光的波动说。光之波动说的确立有两个关键证据。1801 年英国人托马斯·杨参照水波干涉所做的光双缝干涉实验，得到了如同波浪高低起伏的明暗相间条纹(图2)。1815 年法国人菲涅尔从惠更斯原理，即波前上的每一点都可以作为次级波源，出发，对杨的实验结果给出了计算上的证实。菲涅尔的计算还预言，在光路上的圆形小物体，其所造成的阴影中心是亮的。该预言于1817年被实验观察证实。

对双缝干涉实验的所谓计算解释，其关键词就是三角函数之和。对函数eikx - ωt + eik(x + Δx) - ωt 求模平方，可得周期函数2 + 2cos kΔx ，干涉条纹的明暗相间就是用这个函数解释的。当然了，对这个公式不可过于当真，即便计入狭缝的衍射效应所得到的强度分布公式也不能严格拟合实验得到的强度分布，而所谓的干涉花样强度分布的实验测量，本身就是个有趣的、困难的话题。

不管怎样，光的波动说建立起来了。基于波的概念，或者说基于三角函数表示的振荡及一些其它信念，许多光的现象可以被解释得相当令人满意。此时的光是一种波，是某种物质的振动(vibration)。

4 麦克斯韦方程组与电磁波  

在1861—1862 年间，英国人麦克斯韦在总结前人电磁学研究的基础上，得到了一组方程

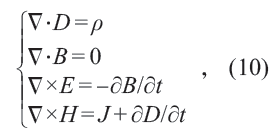
其中第四个方程中的∂D/∂t 项被称为位移电流，是麦克斯韦添加上去的。1865 年，麦克斯韦得到了关于电磁场的波动方程

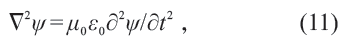
其中的波速c = (μ0ε0)-1/2 具有和当时测得的光速大抵相近的值。这自然导致两个具有重要物理意义的问题：

1)电磁场可以是波?

2)电磁波的波速等于光速？如果是，这意味着光是电磁波？

记住，对于此时的麦克斯韦，方程(11)描述的电磁波依然是个机械的概念。

1887 年，德国人赫兹用图3 所示的装置在电路旁边的用一根导线连着的两个锌球之间引起了电火花，这说明电磁场从线路中溢出来了。这个实验被看作是第一次产生了电磁波，不过也许同样重要的是，它第一次让人们注意到了光电效应。既然实验产生了电磁波，且速度就是光速，且还存在大量的光—电和电—光效应，认为光是电磁波就是水到渠成的了。

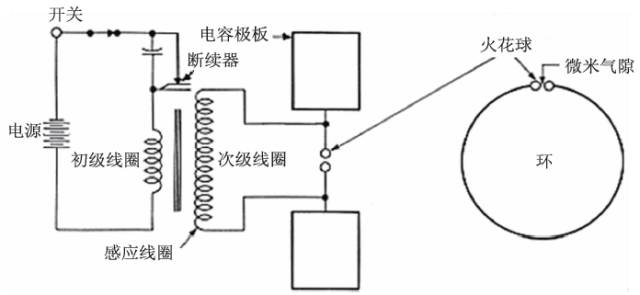
图3 赫兹产生电磁波所用电路的示意图

所谓的用电路产生电磁波，电磁波是由电子经加速后向外辐射的。向空间辐射不同花样的电磁波，要求设计不同样式的发射天线；当然出于接收电磁波和探测电磁波源的考虑，人们也设计了各色各样的接收天线。确立电磁波的来源，从来都不是一个简单的问题。

寻找光，现在是电磁波了，之振动实体或曰介质的过程是物理学史上的重大叙事。Michelson—Morley 实验的无结果表明，没有地球对光以太的相对运动。此实验被当作否定光以太存在的证据。今天的观点是，电磁波是场，它本身就是存在，它凭借自身向远处传播。

5 光的粒子说、物质波与量子力学波函数  

1900 年，普朗克从熵概念出发成功拟合了黑体辐射的实验曲线，其后顺着玻尔兹曼的统计物理思路也得到了该拟合曲线。后一条思路用到了一个重要的前提，即频率为ν的光，其基本能量单位是hν。这是1877 年玻尔兹曼假设的再现。1905 年，爱因斯坦往前更进了一步，他假设如果频率为ν的光之能量是被固体按照hν一份一份地吸收的，则光电效应的系列实验结果就能得到完满的解释。此外，康普顿研究了电子对X-射线的散射，确立了光的能量量子还对应明确的动量h/λ。到此，原先比照水波概念的光波，有理由被当作粒子(particle)了。注意，此时光是粒子(particle)的观念同牛顿的光微粒说还是有些区别的：比如，它有明确的频率或者波长的概念，其能量和动量则分别是固定的hν和h/λ。常数h 被称为普朗克常数。

光是波还是粒子的观念激发了法国人德布罗意的灵感：如果光既是(水)波又是粒子，那么作为粒子的电子是否也是波，或者说也会表现出波的行为？1924 年，德布罗意提出了物质波的概念：电子这样的粒子也是波，相应的波长和频率由粒子的能量E和动量p给出

1927 年美国人Davidsson 和Germer 用电子束照射到镍晶体上，获得了如同X-射线晶体衍射那样的花样，算是首次验证了电子的波动性。

德布罗意的物质波概念随着他的博士论文被送到了德国和瑞士。据说爱因斯坦对物质波的概念非常欣赏。劳厄认为关于物质波总该有个波动方程，薛定谔接受了为物质波构造方程的挑战并在1926 年分四部分发表了题为《作为本征值问题的量子力学》的论文，提出了量子力学的波动方程

其中，算符H是系统的哈密顿量，而函数ψ(x，t)是粒子的波函数。波函数是关于时空的复函数，其模平方为粒子在空间某处出现的几率密度——如果这波函数可以归一的话。

粒子是波或者会表现出波动行为的想法，结果导致了量子力学以及波函数的概念。根据量子力学，粒子的所有物理信息都被包含在描述其状态的波函数中了。考察如下的一维谐振子的波函数

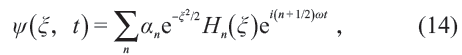
虽然仍可见类似eiωt 那样的因子，但却没有ei(kx - ωt)这样的因子了。这一点也不妨碍我们把(14)式中的函数称为波函数。量子力学带来了物理学的革命，也彻底改变了人类社会，至于其波函数中不(必然)含有ei(kx - ωt) 这样的描述波动的因子，那有什么关系。波函数到底是什么， 重要吗？嗯……，不重要吗？

与对应(7)式那样的经典平面波表示ψ ∝ ei(kx - ωt)相比，量子力学平面波函数

ψ ∝ ei(p̂⋅x̂- Et) /ℏ具有更多的内容，其中t 是作为参数的时间，E是体系的能量，对应哈密顿算符H；而x̂是位置算符， p̂是动量算符，两者还要满足量子化条件[x̂，p̂]=iℏ ；ℏ = h/2π ，h是普朗克常数，是量子力学的标签。

量子力学带来更多的认识。考察一维自由粒子，其哈密顿量为

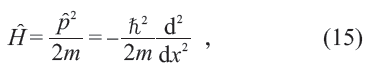
相应的定态薛定谔方程为

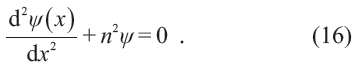
满足波函数要求的形式解为cos(nx)， sin(nx)，x ∈(x0，x0 + 2π ) 。根据量子力学(的数学)，此处的哈密顿量是一个自伴随算符，其所有本征函数构成了一个完备正交基，即是说对于任何定义在(0，2π)上的函数f(x)，有

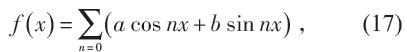
这分明是傅里叶级数展开。

6 傅里叶分析  

傅里叶级数是法国人傅里叶在研究传热问题时得到的。(17)式形式的展开威力巨大，连锯齿状的或者平台状的严重非光滑函数都可以根据(17)式展开成光滑的三角函数的级数——这个不可思议的特点最是它令人难以接受的地方。进一步地，对于时间的函数s(t)，一般有傅里叶变换

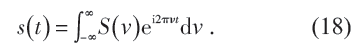
注意，此处与时间共轭的频率变量也是连续的。

有了傅里叶分析，一般的时空变量的函数f (x，t) 都能表示为sin(kx - ωt) 形式的函数对k，ω的求和或者积分。一条毫无变化的水平线经过傅里叶分析，如果只看其有限的傅里叶展开项，也成了波了，如果波指的是sin(kx - ωt) 形式的三角函数的话。在分析实践中， 某个时空函数f (x，t) 在固定点上表现为时间序列f (x0，t) ，它可以按照(18)式被分析为是由具有某频率谱的波叠加而成的。探测到一个时间序列，将之解释为对波的探测，除了会作傅里叶分析的功夫，还要有其它的辅助性信念。

傅里叶分析容易让人想起托勒密的epicycleon-deferent 理论，汉译本轮—均轮理论。圆周运动上叠加圆周运动是很容易得到各种可能不是很光滑的图形的，包括棱角分明的三角形——这是数学的威力。

7 相对论与引力波  

在牛顿力学中，在引力质量Mg的引力场中运动的质点(惯性质量为mi，引力质量为mg)，其运动方程为

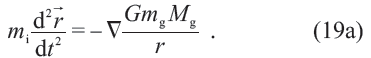
在伽利略变换t ↦ t′ ， r ↦ r′= r - vt + r0 下，此方程形式不变。与此同时，电磁学的波动方程(11)则是在洛伦兹变换

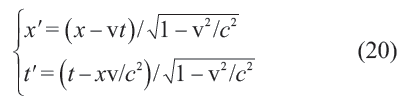
下保持形式不变；或者说，变换(20)保持(光的)时空距离函数

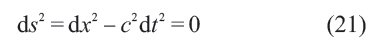
不变。此为狭义相对论。显然，经典电磁学和引力的方程遵从不同的变换规律，这表明物理学内部尚不协调。爱因斯坦决定把狭义相对论也应用于引力问题，为此要把狭义相对论加以推广(generalized)。广义相对论建立在两个等价原理上。所谓的引力质量与惯性质量等价，是说方程(19a)可以约化为

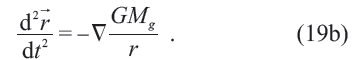
这里方程的左边是一个运动质点的加速度，右边则是该质点遭遇的引力场。加上所谓的引力与加速度之间的等价(意思是说19(b)可以移项)，而加速度可以从运动轨迹的曲率中得到，因此关于引力的描述就转化成了关于弯曲时空中路径之曲率的表述。

爱因斯坦根据以上考虑，从弱静引力场出发，于1915年构造出了他的引力场方程

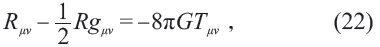
其中gμv 是时空的度规， Rμv 是由gμv 得到的Ricci张量，T 是动量—能量张量。方程(22)于1916 年正式发表，目前只有Schwarzschild 解和Kerr 解这两个严格解，这可能是因为方程(22)要满足微分同胚协变性，是高度非线性的缘故。与高度非线性的方程(22)相比，经典波动方程和量子力学的薛定谔方程，甚至狄拉克方程，可都是线性的，那里得到的波，或者说(虚)变量x - vt 的三角函数，作为方程的解，还是容易的。

对方程(22)作弱场近似，即考察远离大质量分布的几乎平坦的区域，将其度规gμv写成gμv=ημv+hμv 的形式，其中ημv=(1，1，1；－1)是平直时空(闵可夫斯基时空)的度规，得到近似方程

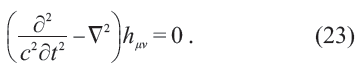
附加的规范条件为h0μ=0；hμμ = 0 ( 横波， 迹为零)。显然，(23)和方程(11)具有完全相同的形式，描述的是速度为c 的横波。此即为引力波方程，此波振荡的主体是张量hμv=gμv－ημv。或许如同量子力学波函数ψ，hμv也是一个需要诠释但未被正确诠释的量。注意，所谓的引力波具有光速的说法，几乎不具有任何特别的物理意义。爱因斯坦在构造广义相对论时，本来就是在推广狭义相对论，要求弯曲时空的局部满足洛伦兹变换，因此这个参数c 是从一开始被加进去的。如果真有什么独立的、无心插柳式的实验，能得到与光速误差在一两个数量级内的时空度规振荡的相速度或群速度，那才真是对广义相对论的强力支持。

8 结语  

本文检讨了自经典力学的机械波到广义相对论的引力波的诸多波概念。一个事实是，在各种不同语境中出现的波概念，其关切的物理量所涉及的物理现实与数学结构，后者还包括具体方程的形式和波的函数表达，还是有许多或细微或深刻的区别的。在物理学中，波既被当作运动的形式，也被当作存在自身的形式，其实本质上也不过是一个在我们有限的数学知识内容易掌握的工具形式。在真实的物理世界中，一根金属丝除了会象三角函数那样来回伸缩，它还会永久变形甚至断裂；水面上除了有贝塞尔函数那样的圈状波纹以及用双曲函数描述的孤立波，也有能打翻大船的湍流；电磁场除了会优雅地振荡着飞越真空，它还真能击穿空气产生闪电……。物理的现实，不局限于形式简单的数学解。

波的概念，是物理学入门处第一根被具象化了的虚拟支柱，而已。

审核编辑：汤梓红