SPC控制图为什么是±3σ

SPC控制图就是一个预警系统，预警系统都存在两类风险：第一类风险是误报警风险（第一类错误）α，第二类风险是漏报警风险（第二类错误）β。

两类风险：

α风险：

即使过程时候处于受控状态，由于偶然原因也可能有某些点落在控制限之外，如果判断为异常，那么这个判断是错误的，其发生概率为α。在3σ方式下，α=0.27%。如下图所示：
 

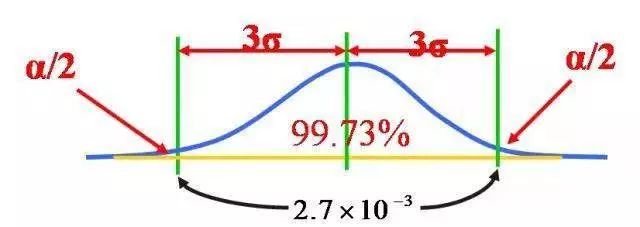
β风险：

如果过程是异常，但也会有部分点位于控制界限内，如果抽取到这样的产品，就会被判断为正常，从而犯了第二类错误，即漏发警报。犯第二类错误的概率记为β。如下图所示：
 

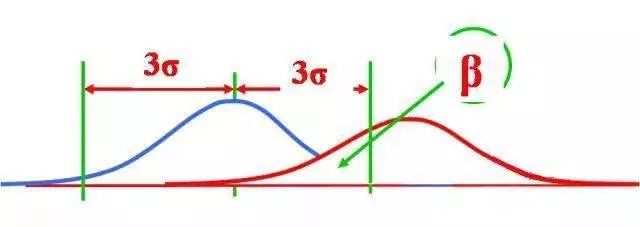
如何减少两类错误所造成的损失？调整UCL与LCL之间的距离可以增加或减少α和β。若此距离增加则α减少，β增大；反之则α，增大，β减少，请参考上述两个图。

举例

举例来说，我们按照μ±3σ的规则，如果发现数据点在μ±3σ之外，我们认为这个数据点是异常的，但我们这个判定是错误的概率是α，即0.27%，少于统计学中的5%的显著性水平。

一个解决方案是：根据使两种错误造成的总损失最小的原则来确定UCL与LCL二者之间的最优间隔距离。经验证明：休哈特所提出的3σ方式较好，在不少情况下， 3σ方式都接近最优间隔距离。

下图列出μ±nσ的1-α的概率。

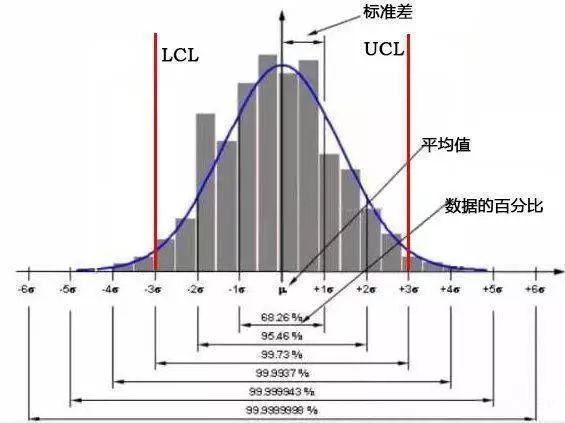
因为常规控制图的设计思想是先确定犯第一类错误的概率α，再确定犯第二类错误的概率β。

按照3σ方式确定CL、UCL、LCL就等于确定了α =0.27%；在统计中通常采用α=1%，5%，10%三级，但休哈特为了增加使用者的信心，把常规控制图的α取的特别的小，这样β就比较大，这就需要增加第二类判异准则，即便点在控制限内，但当点排列不随机也表示存在异常因素。

这就是为什么常规控制图的异常判定准则有两类，即：点超出控制限就判异和控制限内点排列不随机判异两类。

编辑：黄飞