基于系统密度泛函理论计算建立锂硫电池中SRR的电催化模型

01、导读

锂硫（Li-S）电池理论能量密度高、成本低，是最有前途的储能系统之一。然而，放电期间从Li2S4到Li2S的缓慢还原动力学阻碍了Li-S电池的实际应用。尽管已经提出了各种电催化剂来改善反应动力学，但由于硫还原反应（SRR）的复杂性，其电催化机理尚不清楚。因此，深入了解电催化机理对于设计先进的电催化剂至关重要。

02、成果背景

近日，Angewandte Chemie International Edition上发表了一篇题为“An Electrocatalytic Model of the Sulfur Reduction Reaction in Lithium–Sulfur Batteries”的文章，该文章以杂原子掺杂碳材料为例，基于系统密度泛函理论计算，建立了锂硫电池中SRR的电催化模型，揭示了SRR的化学机制。LiSy∙(y=1,2或3)自由基的吸附能被用作预测反应路径、速率决定步骤和过电位的关键描述符。该研究为探索复杂的SRR机制和设计高性能锂硫电池电催化剂提供了一个的理论模型。

03、关键创新

（1）本工作建立了一个电催化模型，用于探索SRR（Li2S4→ Li2S）；

（2）通过LiSy∙自由基（y=1、2或3）吸附过程中的吉布斯自由能变化（ΔGradical），可以确定SRR在工作电位下的速率决定步骤和能垒；

（3）最后，建立了η与ΔGradical值的关系图，以指导先进SRR电催化剂的设计。

04、核心内容解读

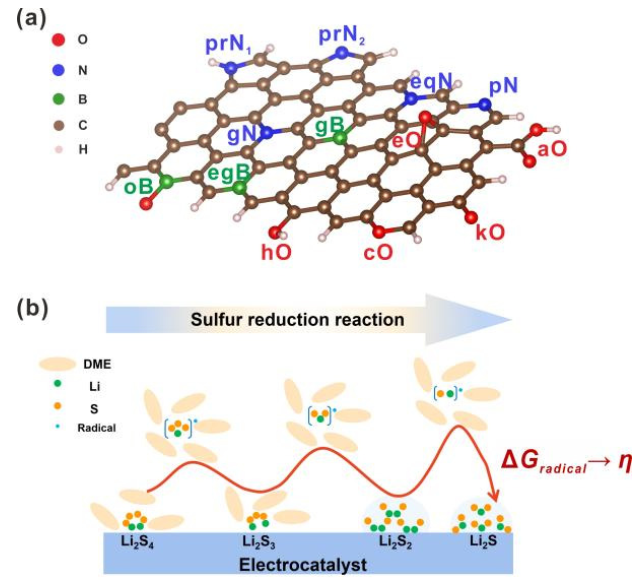
图1. （a）杂原子掺杂石墨烯纳米带（X=O，N，B）和（B）锂硫电池第二放电平台的反应机理示意图。@Wiley

杂原子掺杂GNR（X掺杂GNR）因其优异的导电性和在锂硫电池中具有良好的电催化活性而被选为本工作中的电催化剂模型。通过将三种非金属元素（X=N、O和B）取代边缘或体相碳原子引入石墨烯基体，构建了一系列周期性GNR模型。考虑了13种掺杂剂（图1a），包括酮基（kO）、羧基（aO）、羟基（hO）、环氧基（eO）、环氧（cO）、石墨氮（gN）、吡啶氮（pN）、C–N–C型氮（eqN）、吡咯烷氮（prN1）、无氢吡咯烷（prN2）、石墨硼（gB）、B–2C–O型硼（oB）和C–B–C型硼（egB）。

由于SRR（图1b）是六电子还原反应（Li2S4+6Li++6e−→4Li2S），整个转化过程分为六个基本步骤，生成一系列LiSy∙自由基和Li2Sy分子。考虑到不同的溶解度，可溶性Li2S4、Li2S3和LiSy∙自由基在DFT计算中被视为分子，而不溶性Li2S和Li2S2被视为晶体。

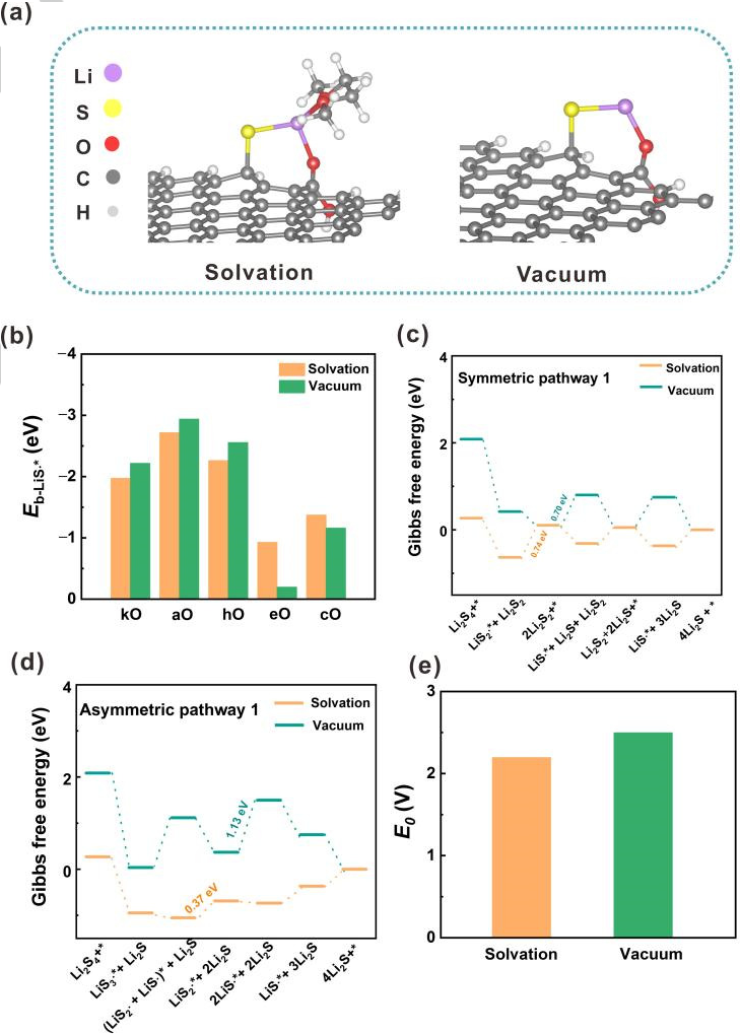
图2. 溶剂化和真空模型之间的比较。（a）LiS∙自由基的吸附构型，左：溶剂化模型；右：真空模型。（b）LiS∙自由基在氧掺杂GNR上的吸附能（Eb）。在（c）对称和（d）不对称路径中，U=2.15 V（vs.Li/Li+）时的自由能图。（e）锂硫电池第二平台的计算平衡电位。@Wiley

由于溶剂化效应在调节溶液中分子结构和反应行为中具有重要作用。因此，采用溶剂化模型与真空模型进行比较（图2a）。具体地，使一个或两个1，2-二甲氧基乙烷（DME）分子分别与可溶性LixSy（x＝1或2；y＝1、2、3或4）自由基和分子相互作用。真空模型和溶剂化模型在含硫物质的吸附能、SRR过程的速率决定步骤和锂硫电池第二放电平台的计算平衡电位（E0）方面表现出巨大差异。

首先，比较溶剂化和真空模型下的LiSy∙自由基吸附能，以O掺杂GNR为例（图2b）。尽管在两种模型中，LiSy∙自由基在O掺杂GNR上的吸附强度呈现出相同的趋势，但溶剂化效应可以减弱或增强吸附。一般而言，在溶剂化模型中，掺杂kO、aO和hO的GNRs对LiS∙自由基的吸附能比在真空模型中要小约0.25 eV，而eO掺杂的GNR的吸附能增加0.73eV。在掺杂O的GNRs上，LiS2∙和LiS3∙自由基也观察到类似的现象。。

其次，溶剂化效应可以调节SRR过程中的速率决定步骤。速率决定步骤被定义为在平衡电位下ΔG最大的步骤。以O掺杂GNR的SRR为例（图2c、d），第二步是溶剂化模型中aO和hO掺杂GNRs的速率决定步骤。然而，在真空模型中第三步成为速率决定步骤。

第三，这两个模型表现出非常不同的第二平台E0。溶剂化模型的E0（2.19 V）与实验恒流间歇滴定技术的结果（2.10 V～2.20 V）极为相似。相反，真空模型的误差为0.34 V（图2e）。上述结果表明，溶剂化效应在探究SRR机理中发挥了极其重要的作用，因此将溶剂化模型用于进一步的计算。

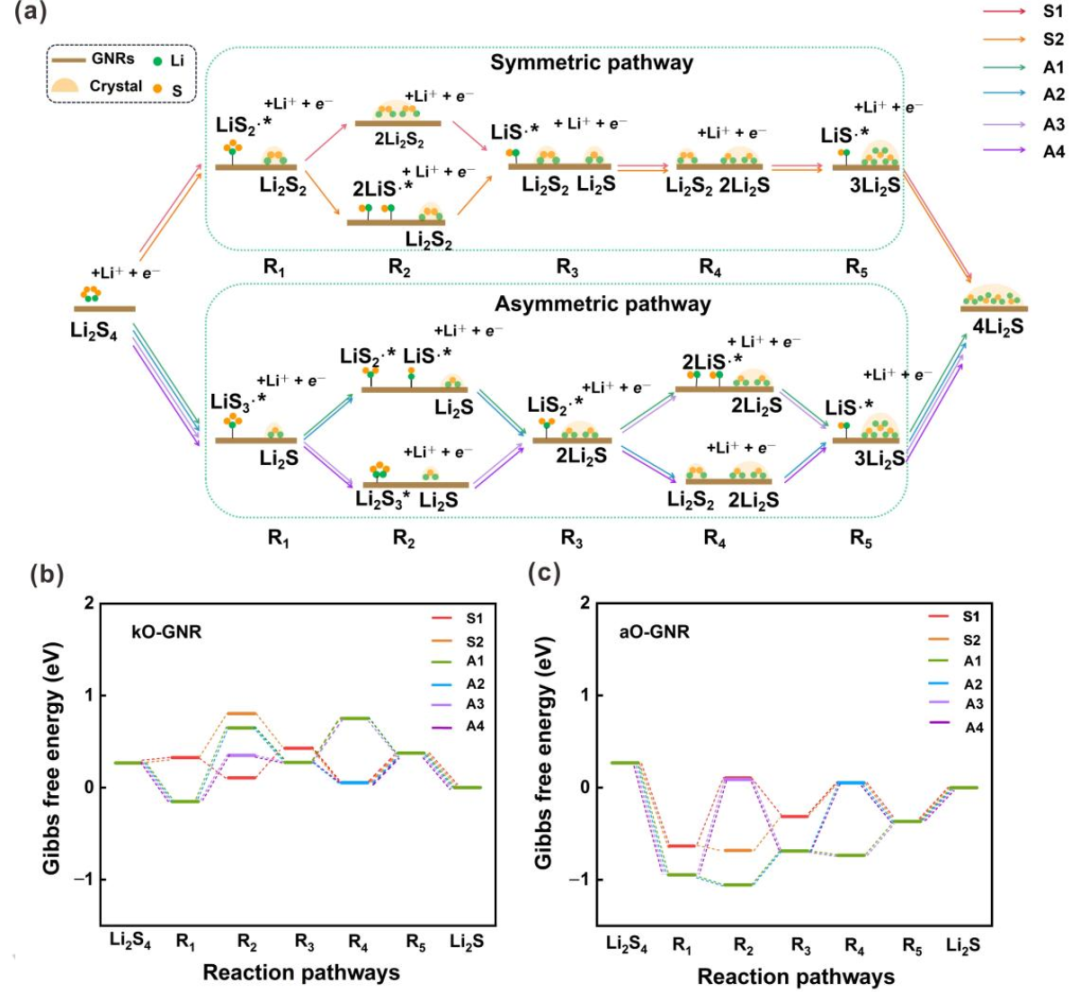
图3. SRR过程反应机理的探索。（a）所有可能反应途径的示意图。（c）掺杂kO的GNR和（d）掺杂aO的GNG上六种可能路径在U＝2.15 V（vs.Li/Li+）下的自由能图。S1–S2、A1–A4和R1–R5分别代表SRR过程中的对称路径、不对称路径和反应中间体。@Wiley

通常，根据Li2S4分解机理，SRR反应可主要分为两类，即对称路径和不对称路径。然而，一些中间态总是比它们的最终产物具有更高的能量。例如，不对称路径中R1有两种可能的状态，即LiS3∙*+Li2S和LiS∙*+Li2S3（*表示该物质吸附在电催化剂上）。对于所有GNR，上一个总是比下一个更稳定。因此，在排除不可能的路径后，可以大大简化整个反应路径（图3a）。在简化的机制中，Li2S4被还原为LiS2∙自由基和Li2S2，最后是对称路径中的Li2S。然而，Li2S4被还原为LiS3∙自由基和Li2S，最后是不对称路径中的Li2S。因此，SRR路径可以进一步细分为两个对称路径（S1和S2）和四个不对称路径（A1–A4）。

在对称路径中，LiS2∙*首先由吸附在表面上的Li2S4产生。然而，LiS2∙*分别在对称路径S1和对称路径S2中的第二步转化为Li2S2固体或两种LiS∙*。在第三和第五步中，Li2S2固体可以进一步还原并产生吸附自由基LiS∙*和Li2S固体。LiS∙*随后在第四和第六步中转化为Li2S固体。随后的四个步骤对于S1和S2路径是相同的。因此，每一步的自由能变化（ΔGi）由等式（1）计算：

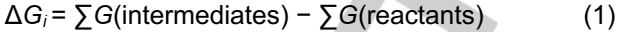
其中∑G（中间体）和∑G（反应物）分别表示每个中间体和反应物的吉布斯能之和。基于每个ΔGi的值，可以通过U=2.15 V（vs.Li/Li+）下的能量分布来探索SRR的反应机理（图3b、c）。对称路径S1在第二和第五步的能量变化比路径S2低。因此，在对称分解机制中，路径S1是优选的。

与对称机制相比，包括四种不同分解路径的不对称机制要复杂得多，涉及更多中间体（图3a）。吸附的LiS3∙*自由基在所有四种路径的第一步形成，但可以在以下步骤中进一步转化为不同的中间体。在不对称路径A1和A2中，LiS3∙*在第二步分解成LiS2∙*和LiS∙*自由基，LiS∙*自由基随后转化为Li2S固体。而在不对称路径A3和A4中，第二步是形成Li2S3中间体，并进一步产生吸附的LiS2∙*自由基。在第四步时，LiS2∙*进一步分裂为两个LiS∙*自由基，LiS∙*自由基在不对称路径A1和A3中再次转化为Li2S固体。然而，在不对称路径A2和A4中，LiS2∙*在第四步中进一步还原为Li2S2固体，并生成LiS∙*。最后，LiS∙*在第六步中转化为Li2S固体。根据能量分布（图3b、c），不对称路径A1在第三、第四、第五和第六步的能量变化低于其他不对称路径A2–A4。因此，在不对称分解机制中，途径A1是优选的。

根据U=2.15 V (vs. Li/Li+)时的能垒进一步考虑对称路径S1和非对称路径A1之间的竞争关系。aO、hO、pN、eqN、oB和egB掺杂的GNR更倾向于不对称途径A1，这表明在这六个X掺杂GNR上优先产生LiS3∙*。相反，其他7个掺杂X的GNRs产生固体Li2S2的主要路径是对称路径。

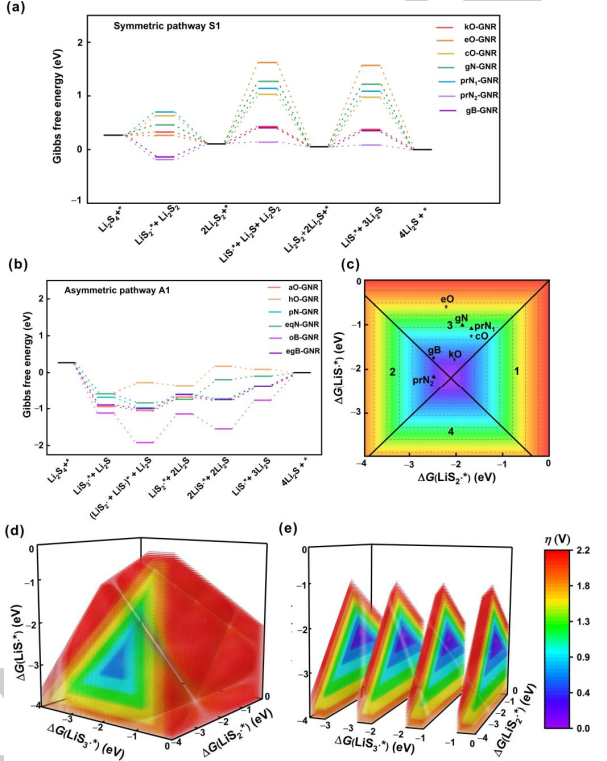
图4. SRR的电催化模型。遵循（a）对称路径1和（b）不对称路径1的X掺杂GNR在U=2.15 V（vs.Li/Li+）下的自由能图。将过电位与自由基在经历（c）对称路径和（d）不对称路径GNR上的吸附吉布斯自由能联系起来的区域图。（e）图d的切片图。@Wiley

图4a、b给出了在2.15 V vs. Li/Li+条件下最有利反应机理的自由能分布，用以比较不同杂原子掺杂的GNRs催化活性。第一步，吉布斯自由能随着电势的增加而上升，被视为SRR过程中的速率决定步骤。对称路径为不同电催化剂提供了不同的速率决定步骤（图4a）。具体而言，Li2S2固体转化为LiS∙*, 步骤3或步骤5是分别具有0.32、1.52、0.92、1.16、1.03和0.30 eV能垒的kO、eO、cO、gN、prN1和gB掺杂GNR的速率决定步骤。Li2S2形成的第二步是prN2掺杂的GNR速率决定步骤，能垒为0.30 eV。 进一步构建区域图，以提供探测SRR机制的原则（图4c–4e）。LiS3∙、LiS2∙和LiS∙自由基在电催化剂上的吸附吉布斯自由能分别为ΔG(LiS3∙*)、ΔG(LiS2∙*)和ΔG(LiS∙*)。η和相应的速率决定步骤可从这三个描述符中得出。在对称路径中，η值由ΔG(LiS2∙*)和ΔG(LiS∙*)决定。得到的二维(2D)图呈金字塔形状，可分为四个区域，代表四个不同的速率决定步骤(图4c)。具体来说，当ΔG(LiS2∙*)和ΔG(LiS∙*)在区域1或2相交时，η与ΔG(LiS2∙*)呈现火山图关系。当ΔG(LiS2∙*)比−2.23 eV更正时，步骤1是电位限制步骤，而ΔG(LiS2∙*)比−2.23 eV更负时，步骤2是电位限制步骤。同样，当ΔG(LiS2∙*)和ΔG(LiS∙*)在区域3或区域4相交时，催化活性可以用η与ΔG(LiS∙*)相关联的火山图来描述。当ΔG(LiS∙*)比−2.18 eV更正时，电位受到步骤3的限制。当ΔG(LiS∙*)比−2.18 eV更负时，步骤4为电位限制步骤。二维图中的连接点对应两个火山顶部η=0 V的点，ΔG(LiS2∙*)和ΔG(LiS∙*)分别等于−2.23和−2.18 eV。如图4c所示，prN2和gB掺杂的GNR在对称路径中的其他GNR中表现出最低的过电位（0.34 V），这得益于LiS2∙(掺prN2和gB的GNR分别为−1.22和−1.17 eV)和LiS∙(掺prN2和gB的GNR分别为−2.41和−1.99 eV)良好的折中。 在非对称机制中，图被绘制为ΔG(LiS3∙*)、ΔG(LiS2∙*)和ΔG(LiS∙*)的函数，表示为一个三维(3D)图(图4d)。类似地，给定催化剂的活性可以直接从3D图中获得。具体地说，速率决定步骤和η可以通过固定不同的描述符来实现。3D图被分割成几个2D图，整合了其他两个描述符（ΔG(LiS2∙*)和ΔG(LiS∙*))（图4e）。通过2D图中心部分的尺寸和颜色得到速率决定步骤和η，这取决于固定的ΔG(LiS3∙*)。 对于掺杂了hO和eqN的GNRs，决定速率步骤是LiS2∙*分解为LiS∙*，最大η分别为0.58和0.61 V。对于aO、pN、oB和egB掺杂的GNRs，决定速率步骤是Li2S2分解为LiS∙，最大η值分别为0.41、0.42、0.82和0.43 V。最大η由三个描述符控制(ΔG(LiS3∙*)、ΔG(LiS2∙*)和ΔG(LiS∙*))。结果表明，在不对称机制下，最佳的电催化剂应具有理想的吸附吉布斯自由能平衡，对于ΔG(LiS3∙*)、ΔG(LiS2∙*)和ΔG(LiS∙*)分别为−2.20、−2.25和−2.15 eV，从而产生较小的过电位。

05、成果启示

本工作通过DFT计算系统地研究了锂硫电池中的SRR机制，并建立了电催化模型来预测电催化剂的活性。在电催化模型中全面讨论了对称和不对称机理。前者是指由Li2S4直接生成Li2S2，而后者则经历了有Li2S3的路径。LiSy∙自由基的吸附吉布斯自由能是确定SRR过电位和速率决定步骤的关键描述符。因此，综合考虑了三个描述符(ΔG(LiS3∙*)、ΔG(LiS2∙*)和ΔG(LiS∙*))，构造了一个区域图模型来可视化过电位和速率决定步骤。该研究在原子水平上建立了SRR电催化模型，加深了对SRR机理的理解，从而可以实现先进SRR催化剂的合理设计。

审核编辑：郭婷