RC电路耦合、相移、滤波、微分、积分的知识

所谓RC电路，就是电阻R和电容C组成的一种分压电路。如下图1所示：输入电压加于RC串联电路两端，输出电压取自于电阻R或电容C。由于电容的特殊性质，对下图(a)和(b)不同的输出电压取法，呈现出不同的频率特性。

由此RC电路在电子电路中作为信号的一种传输电路，根据需要的不同，在电路中实现了耦合、相移、滤波等功能，并且在阶跃电压作用下，还能实现波形的转换、产生等功能。所以，看起来非常简单的RC电路，在电子电路中随处可见，有必要对它的基本应用加以讨论。

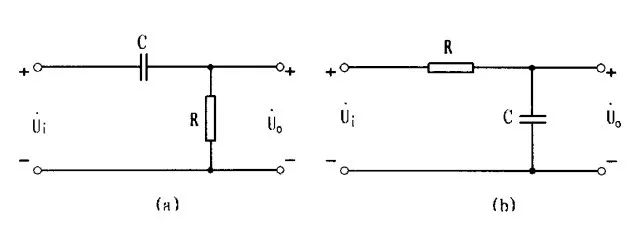
图1：基本RC电路  1RC耦合电路

RC耦合电路即阻容耦合电路，是多级放大器级间耦合方式的基本形式。如下图2所示为两级放大器，第一级的输出电压就是通过如下图3所示的RC阻容耦合电路加到第二级上的，其中C=C2，R为R5与rbe2 + ( 1+β) R6的并联，Ui就是第一级的空载输出电压，Uo就是第二级的输入电压。实际上整个放大器的输入耦合电路、输出耦合电路都是一个输出电压取自于电阻的如图3所示的RC耦合电路。对这种耦合电路输出电压可表示为：  

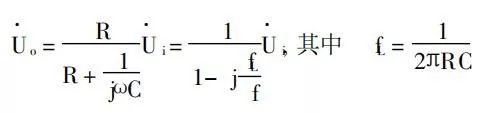
  当传输信号的频率很高时，即：f＞fL时:Uo=Ui，即第二级得到的输入电压等于第一级的输出电压，耦合电容相当于通路。即这种情况下，RC耦合电路将被传输的信号无衰减地、且无相移地由上级耦合到下级。   当被传输信号的频率降低到f=fL时:输出电压的大小等于输入电压大小的1/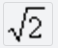且相位超前45度。由通频带的概念，这就是下界频率。由上可见，RC电路作为耦合电路，能否将被传送的信号顺利地耦合下去，完全由被传送信号频率和RC电路的参数比较后决定的。一般来说，RC电路的时间τ=RC远大于被传送信号的周期T，即被传输信号的频率远大于由电路参数决定的下界频率时，这种RC耦合电路中的电容相当于通路。  

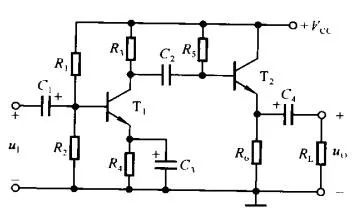
图2：两级放大电路

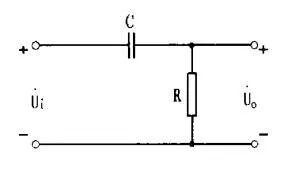
图3：RC耦合电路  2RC相移电路

RC电路作为二端传输网络，若输出电压取自于电阻，则输出电压的相位超前；若输出电压取自于电容，则输出电压的相位落后。这种超前或落后最大可达90度，但此时输出电压的幅值也趋近于0。一般在电路中，使之信号通过RC电路，既有一定的相移，又有一定的电压幅值，这样RC电路就成了一个相移电路。在电路中，根据需要的不同，将若干节RC电路串联去实现对某一频率的信号进行一定角度的相位移动。图4是一个RC相移式正弦波振荡器电路。   三节RC相移电路在振荡电路中，既是正反馈网络，又是选频网络，合理选其电路参数，对某一频率的信号通过RC相移电路，使之每一节的平均相移为60度，总相移为180度，从而满足振荡平衡条件，对这一频率的信号发生振荡。  3滤波电路

滤波电路是一种能使有用频率信号顺利通过，而对无用频率信号起抑制和衰减作用的电子电路。由于电容阻低频通高频的基本性质，滤波电路的基本组成部分仍是一个RC电路，当输出电压取自于电阻时，它就是一个高通滤波器；当输出电压取自于电容时，它就是一个低通滤波器。   为了隔断负载对RC电路的影响，常将RC电路和集成运放组合起来组成有源滤波器，如图5所示为一阶有源低通滤波器电路。将图中的R和C的位置互换，即得到一阶有源高通滤波器。为了使被抑制的频率成分在截止频率以外衰减更快，可以将几节RC电路串联使用，而得到高阶有源滤波器，也可将不同性质的RC电路相互串并联使用，得到所谓带通滤波器和带阻滤波器等。  

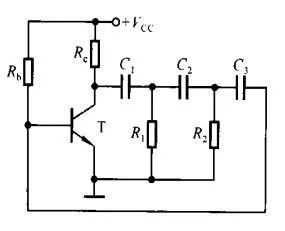
图4：RC相移振荡电路

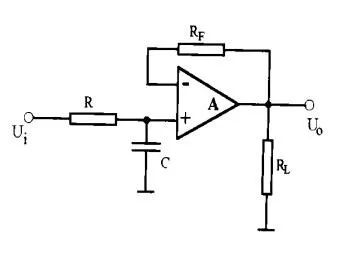
图5：一阶低通滤器  4微分电路和积分电路

前面三个问题讨论的是不同频率的正弦信号通过RC电路时，电路所反映出的性质。当电路中信号电压发生阶跃变化时，由于电容的充放电的性质，使之被传输的信号发生另一种变化，这就微分电路和积分电路。  4.1、微分电路  所谓微分电路仍是一节RC电路，输出电压取之于电阻R。当输入电压为阶跃变化的矩形脉冲时，且RC电路的充放电时间常数τ=RC＜TK(脉冲宽度)时，能将输入的矩形脉冲变成宽度为τ的尖脉冲。如图6所示，由于时间常数远小于脉冲宽度，脉冲上升沿来到时，电容通过电阻R充电，很快充满，电路中的电流变为零，输出电压变为零，由此在R上得到一个与上升沿相对应的正的尖脉冲。   当脉冲下降沿来到时，电容通过电阻R反向放电，同理放电过程很快，在电阻R上得到一个与下降沿对应的负的尖脉冲。由于通过电容的电流为：  

 

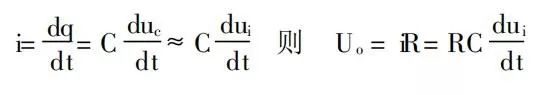
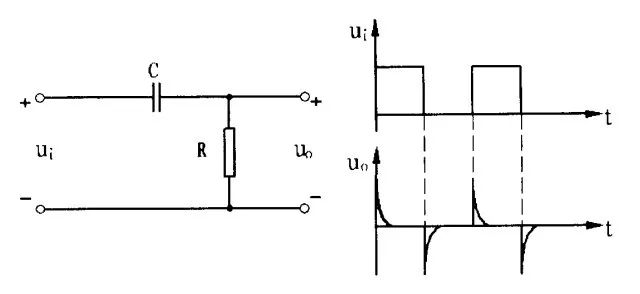
图6：微分电路将矩形脉冲变成尖脉冲   即输出电压近似与输入电压的微分成正比，微分电路由此得名。为使输出电压不受负载的影响，RC电路跟运放组合接成如图7所示的形式，由于运放反向端虚地，输出电压取之于反馈电阻R。微分电路的本质仍是RC电路，运放在此起隔离和缓冲作用。  

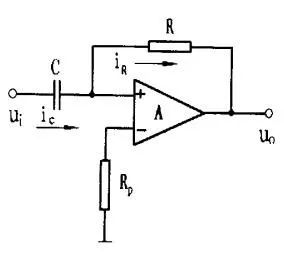
图7：由运放组成的微分电路  4.2、积分电路  与微分电路相反，积分电路中输出电压取之与电容。如图8所示，当RC电路的时常数τ=RC＞TK(脉冲宽度)时，能将输入的矩形脉冲变成幅度随时间线性变化的锯齿波。由于RC电路的充放电时间常数τ远大于脉冲宽度TK，脉冲上升沿来到时，电容通过电阻R充电，远没有充满，即刚经过充电曲线的起始部分，脉冲下降沿来到，电容又开始放电，远没有放完，又在上升沿作用下充电，由此在电容上得到随时间近似成线性变化的锯齿波电压。

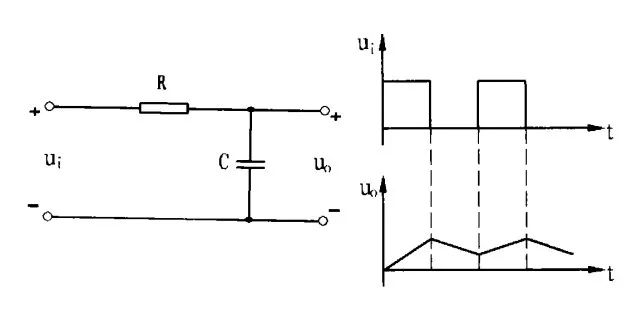
图8：积分电路将矩形脉冲变为锯齿波   因为τ＞TK在输入矩形脉冲的持续时间内，电容上的电压上升不多，即：Uo＜UR，则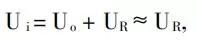： 由此得到：  

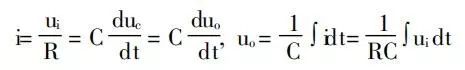
  即输出电压与输入电压的积分成正比，由此得名积分电路。同理，为使RC积分电路不受负载的影响，同样跟运放组合接成如图9形式的电路。运放反向端虚地，输出电压取之于电容。.可见积分电路的本质仍是RC电路，运放在此起隔离和缓冲作用。由上讨论可知：微分电路和积分电路从本质来说都是一节RC电路，微分电路中输出电压取之于电阻，其时间常数远小于脉冲宽度。积分电路中输出电压取之于电容，其时间常数远大于脉冲宽度。  

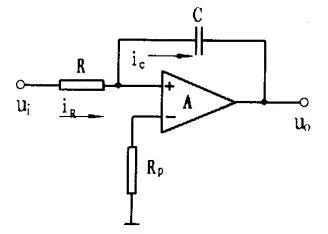
图9：由运放组成的积分电路   除了上述的四种情况以外，还有一种重要的应用，即根据电容充放电时其两端电压的变化情况，在电路中起延时开关作用，在波形产生电路中和定时电路中有着广泛的应用。  5结论

RC电路的本质就是一个分压电路，电路中的传输信号、电路状态发生变化时的跃信号都可作为RC电路的输入电压，根据需要的不同从电阻R或电容C取出输出电压，并根据电容C的充放电性质，巧妙地选取电路参数和电路结构，使RC电路成为电路中信号传输的桥梁，波形变换的转换器，选取有用信号的滤波器或选频网络。  

审核编辑 ：李倩