

使用两点校准消除ADC失调和增益误差
模拟技术
描述
通过示例了解用于补偿模数转换器 (ADC) 偏移和增益误差的两点校准方法和定点实现。
在之前的文章中,我们讨论了可以使用单点校准来消除 ADC 偏移误差。为了补偿偏移和增益误差,我们需要两点校准。在本文中,我们将探讨两点校准方法,并通过示例了解该技术的定点实现。
确定实际 ADC 失调和增益误差的两点校准测试
图 1 显示了受偏移和增益误差影响的单极性 12 位ADC的特性曲线。
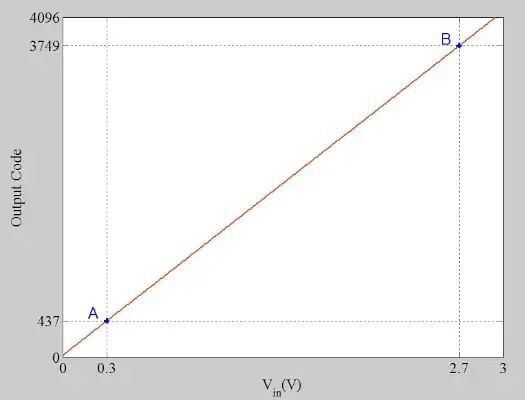
图 1.受偏移和增益误差影响的单极性 12 位 ADC 的特性曲线。
ADC 的满量程值为 3 V。在 ADC 满量程范围的 10% 和 90% 处选择两个测试输入,即点 A 和 B,以确定 ADC 偏移和增益误差。在 0.3 V 和 2.7 V 时,测得的输出代码分别为 437 和 3749。测量传递函数的斜率可以计算为:
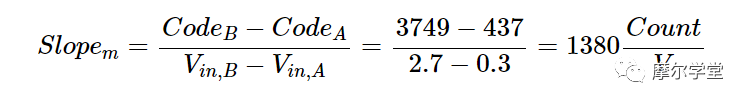
使用点 A 的 x 和 y 值,我们得到以下线性方程:
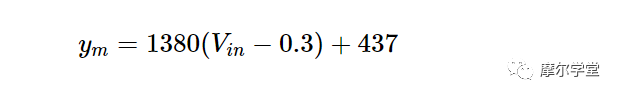
通过代入 V in = 0,可以发现偏移误差为 +23 LSB。下面的等式描述了理想 12 位 ADC 的线性模型:
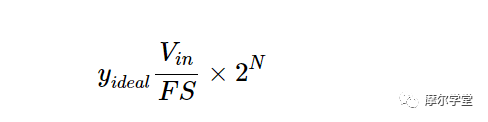
因此,0.3 V 和 2.7 V 时的理想代码值分别为 409 和 3686。使用这些值,可获得理想响应的斜率:
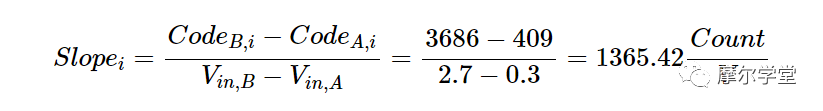
现在我们可以计算ADC的增益误差如下:
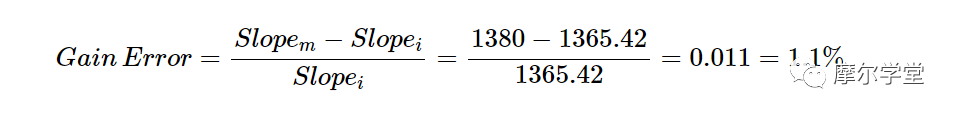
两点校准——修正 ADC 失调误差和增益误差
了解实际响应后,我们现在可以轻松地消除数字域中的偏移和增益误差。首先,我们可以从每个输出代码中减去偏移量,得到一个通过原点且斜率为 Slope m的响应。接下来,将结果乘以 (frac{Slope_{i}}{Slope_{m}}) 围绕原点旋转获得的直线并生成斜率为 Slope i的直线。SlopeiSlopem围绕原点旋转获得的线并产生斜率为 Slope 的直线
这些数学运算将实际响应的直线映射到理想 ADC 的直线。图 2 使用一个夸张的例子来说明校准概念。
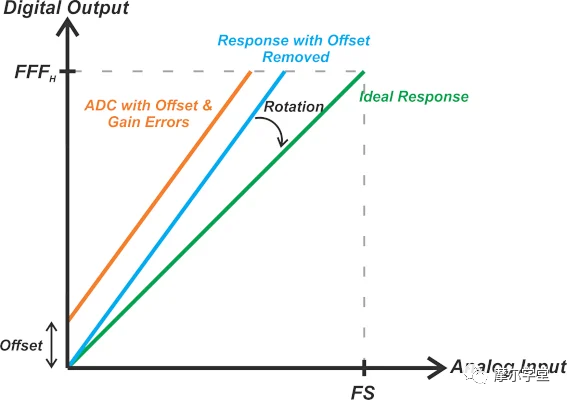
图 2. 显示 ADC 校准的示例响应。
因此,校准后的输出代码 Code Cal可以通过应用等式 1 从实际代码 Code a计算得出:
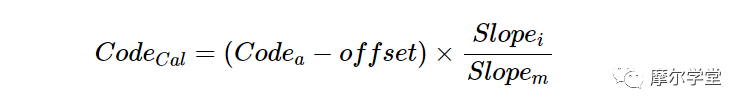
等式 1。
定点校准实现
另一方面,如果我们试图补偿偏移和增益误差的固定值,我们可以简化方程式 1 并实现计算效率更高的系统。继续我们的例子,我们可以将 offset = 23,Slope i = 1365.42,Slope m = 1380 代入等式 1,得到以下关系:
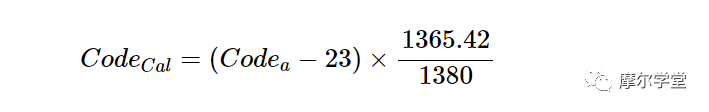
为了节省系统处理器的一些CPU(中央处理器)周期,我们可以将上面的等式简化为等式 2:
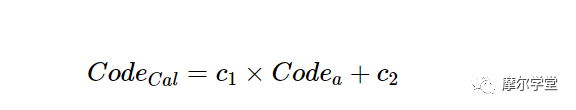
等式 2。
在这里:
c 1 = 0.989434782
c 2 = -22.757
虽然我们可以使用浮点运算来实现上述等式,但定点实现可能更高效且更具成本效益。我们有两个小数,c 1和 c 2。为了以定点格式表示小数,我们将使用隐含的二进制小数点。这意味着我们将假设寄存器的一定数量的位代表整数部分,而其余位代表数字的小数部分。
然后使用 Q 格式符号来指定整数和小数部分的位数。例如,101.0011 可以是 Q3.4 格式的数字,因为它使用三位整数和四位小数部分。
请注意,二进制小数点实际上并未在硬件中实现;这只是一个允许我们在定点处理器中表示小数的概念。此外,给定 Q 格式中的数字可能表示正值或负值。
回到我们的 ADC 校准示例,我们有两个小数,c 1和 c 2,它们应该以适当的定点格式表示。假设使用二进制补码格式的有符号 16 位寄存器来存储这些常量。由于c 1小于1,整数部分只需要一位符号。剩余的位可以表示小数部分,从而形成 Q1.15 格式。
为找到 c 1的定点表示,我们将其乘以 2 15,将其四舍五入为最接近的整数,并将四舍五入的结果转换为二进制形式。
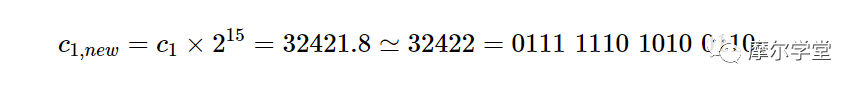
由于 c 2在 16 和 32 之间,我们需要 5 位用于整数部分,1 位用于符号。这为小数部分留下了 10 位。因此,c 2的适当表示是 Q6.10 格式。为了以这种格式表示,我们将 c 2乘以2 10,将其四舍五入为最接近的整数,并将四舍五入的结果转换为二进制形式。
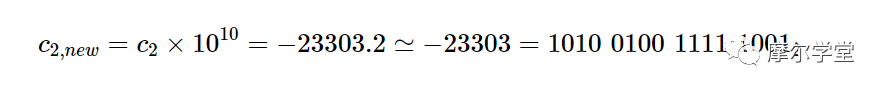
请注意,c 2是二进制补码格式的负数。由于新系数使用不同的比例因子,我们需要仔细跟踪比例因子对我们计算的影响。让我们定义一个新的临时变量 Var 1来存储 c 1、新的和未校准的 ADC 读数的乘积,如等式 3:
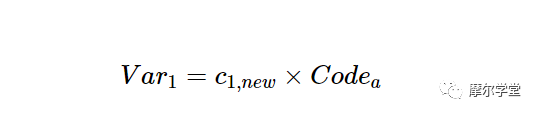
等式 3。
这将产生等式 2 右侧的第一项。假设 ADC 的 12 位输出存储在我们的 C 程序中的带符号 16 位寄存器中。因此,Code a可以认为是Q16.0号码。这意味着实现公式 3 需要将 Q1.15 值乘以 Q16.0 值。变量 Var 1应该是一个 32 位的寄存器来存储这个乘法的结果。此外,由于 Q16.0 数字乘以 Q1.15 值,因此 Var 1为 Q17.15 格式。如果您需要复习使用定点表示的乘法,请参阅本文。
如您所见,乘法运算增加了数据字长。在实现DSP(数字信号处理器) 算法时,我们通常会截断或舍入乘法输出,以防止字长无限增长。然而,在截断或舍入乘法输出之前,我们应该考虑对数据的下一步操作。
在本例中(公式 2),乘法结果将添加到 Q6.10 格式的 c 2, new中。考虑到 c 2, new的小数部分,我们可以丢弃 Var 1的五个最低有效位,并将截断的结果存储在新变量 Var 2中。C 编程中的右移运算符可用于执行此操作:
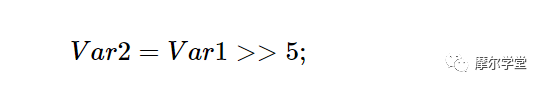
等式 4。
如果我们的系统中有任意长度的寄存器(例如,就像我们在FPGA中那样),我们可以使用 Q17.10 格式的 27 位寄存器存储 Var 2 。但是在C编程中,Var 2还是要存放在一个32位的寄存器中。如果我们截断 Q17.15 数字的五个最低有效位并将结果存储在 32 位寄存器中,我们将获得 Q22.10 数字。最后,我们可以将新的 c 2添加到 Var 2,并丢弃 10 个最低有效位以获得校准的 ADC 值,得到公式 5:
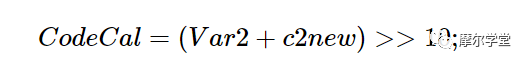
等式 5。
作为旁注,为避免混淆,我想提一下等式 4 和 5 中的变量不使用下标,因为这两行被假定为伪代码。例如,文中的Var 2在方程式4和方程式5中写为Var2。
ADC 定点校准验证
让我们看看上面的定点系数(c 1,new = 32422 和 c 2,new = 23303)是否可以将测得的 ADC 响应映射到理想的直线模型。在图 1 中的 A 点,ADC 输出为 437。应用公式 3,可得 Var 1为:
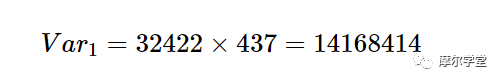
将其转换为二进制格式,右移 5 位,然后找到等效的十进制,我们得到:
Var2=442762
现在,我们添加 c 2,new,并将结果的二进制等效项右移 10 位,得到:
CodeCal=409
您可以类似地验证 B 点也映射到理想代码 3686。请注意,计算机程序使用系数的二进制等效值,我只是使用十进制值来阐明计算。我们可以类似地检查测得的 ADC 响应中的其他点,以确保定点实现产生所需的值。如果不满足,我们将不得不使用更大的寄存器来存储校准系数。
ADC 未使用的输出代码和输入范围
之前,我们讨论了偏移和增益误差会导致未使用的输出代码。上面讨论的校准技术是在 A/D 转换之后执行的。结果,它无法解决未使用的代码问题。为阐明这一点,请考虑图 3 中所示的示例。
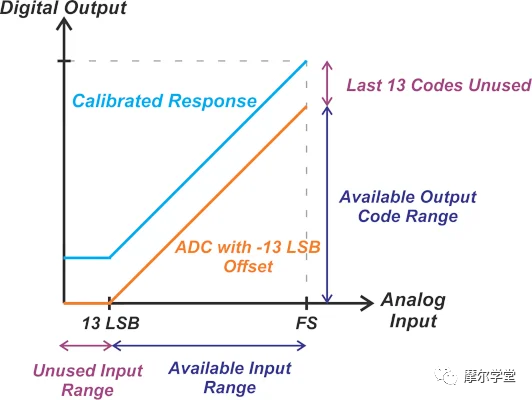
图 3. 显示未使用和可用输入范围和输出代码范围的示例。
在这个例子中,显示了一个偏移量为 -13 LSB 的单极性 ADC。可以通过将 ADC 读数加 13 来校准偏移误差。但是,请注意 ADC 输出小于 13 LSB 的输入值的全零代码。该输入范围在校准响应中仍然不可用,因为校准是在 A/D 转换之后执行的。校准仅向实际 ADC 响应添加恒定偏移,在上例中为所有低于 13 LSB 的值生成代码 13。需要注意的是,一些 ADC 具有与本文讨论的转换后方法不同的内置校准功能。这些内置校准技术可能能够保留 ADC 的原始范围。这种内置校准技术用于 12 位 ADC来自 TI 的TMS320280x 和 TMS3202801x 设备。
审核编辑:汤梓红
-
CYT2B9使用没有偏移和增益调整的ADC,ADC误差会出现A_TEB (+/-12LSB) 吗?2024-01-22 682
-
深度解析精密ADC中的自校准和内部校准2023-12-04 2358
-
AD7403/AD7405的失调和增益误差效应2023-11-29 444
-
基于Arm Cortex-M0+的MCU上的ADC增益误差和失调误差校准2023-09-25 485
-
调整和校准精密DAC中的失调和增益误差2023-02-27 7535
-
了解ADC积分非线性(INL)误差2023-01-27 3151
-
深入探讨模数转换器ADC的失调和增益误差规格2022-12-14 1317
-
了解精密ADC中的自校准和内部校准2022-12-12 2066
-
ADC失调误差和增益误差2022-11-29 1430
-
双极ADC失调误差和增益误差2022-09-13 4299
-
ADC中的增益误差和失调误差的分析2021-04-01 2080
-
如何通过校准来计算和消除增益和偏移误差2019-04-12 7820
全部0条评论

快来发表一下你的评论吧 !

