

傅里叶变换、拉普拉斯变换、Z变换剖析
描述
为什么要读书?
为什么要读书?
书本里,有几千年的哲学观点、有几百年的科学规律、几十年的技术总结。
多读书,可以帮助看明白这个世界,看明白人。
时域、频域、s域、z域
大学《信号与系统》讲了四种域:时域、频域、s域、z域。
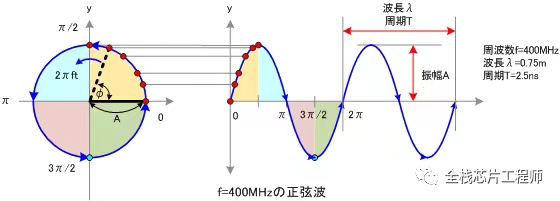
本质上,频域、s域、z域,都是从时域变换到频域。
时域:
连续信号:x(t)
离散信号:x[n]
频域:
连续信号:X(jw)
离散信号:X(e^jw)
转换关系
时域与频域:傅里叶变换
时域与s域:拉普拉斯变化
时域与z域:z变换
频域与s域:jw = s
频域与z域:e^jw = z
为何傅里叶变换?
为什么时域要变化到频域?
当信号从时域变换到频域后。可以观察到很多时域看不到的现象。特别是很多在时域看似不可能的数学操作,在频域反而so easy!
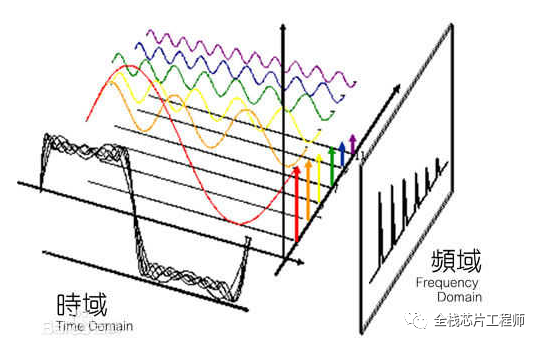
比如,纸上动笔画一个sin(x)函数波形,很简单!
那让你画一个sin(3x)+sin(5x)波形呢?无从动笔?
那给你一个sin(3x)+sin(5x)波形,让你画一个sin(5x)波形呢?
在频域,sin(3x)+sin(5x)就两条竖线!剔除sin(5x)是不是很简单。
从一条曲线中,去除一些特性频率成分,就是信号处理中的滤波。
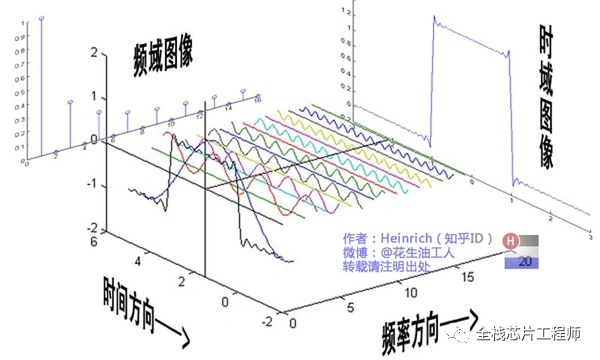
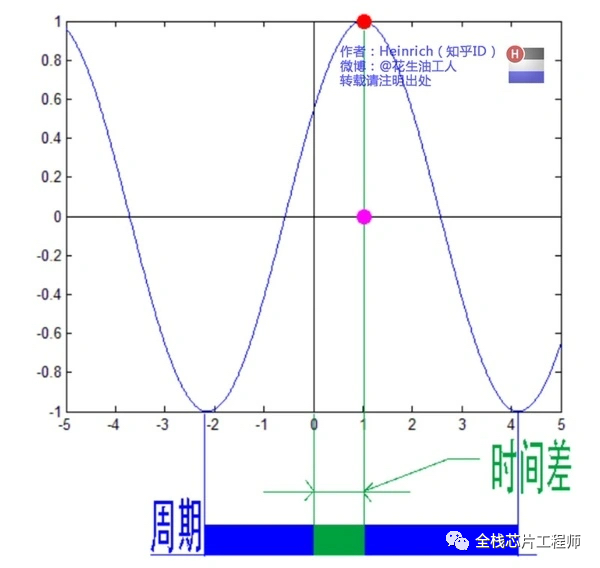
频谱只代表每一个正弦波的振幅,没有相位信息。相位如何表示?
鉴于正弦波是周期的,我们用下图红色点来标记离频率轴最近的波峰:
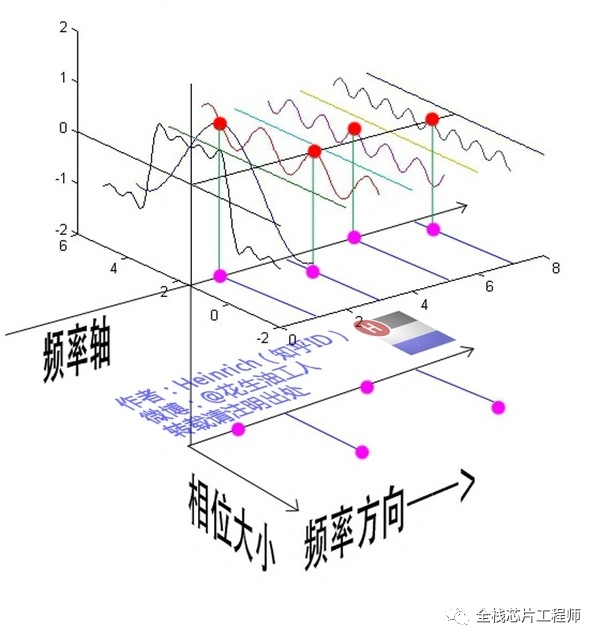
为了看清楚,我们将红色点往下平面投影成粉色点,粉色点与频率轴的距离,这个距离占正弦波的周期的百分比,乘以360°就是相位。
为何要拉普拉斯变换?
为何要拉普拉斯变换?
傅里叶变化只能对能量有限的信号进行变换(也就是可以收敛的信号),无法对能量无限的信号进行变换(无法收敛),因此,拉普拉斯应运而生,在原先的傅里叶变换公式中乘以一个衰减因子,使得无限能量的信号也能进行时频变换。
换而言之,傅里叶变换不能分析系统的稳定性,而拉普拉斯变换转成s域就能分析系统的稳定性。
很多曲线,都可以用这些不同频率,连续旋转的圆,通过线性叠加得到,而傅里叶定律,就是对这个结论的数学描述,傅里叶定律说:只要一个函数满足如狄利赫里条件,都能分解为复指数函数之和,哪怕是如拉格朗日提到的带有棱角的方波函数。狄利赫里条件为:

傅里叶变换有一个很大局限性,那就是信号必须满足狄利赫里条件才行,特别是那个绝对可积的条件,一下子就拦截掉了一大批函数。比如函数f(t)=t^2就无法进行傅里叶变换。这点难度当然拿不到聪明的数学家们,他们想到了一个绝佳的主意:把不满足绝对的可积的函数乘以一个快速衰减的函数,这样在趋于正无穷时原函数也衰减到零了,从而满足绝对可积。
数学描述是:
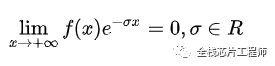

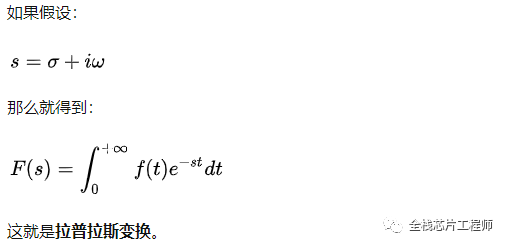
先上图,我们下文讲零极点稳定性问题。
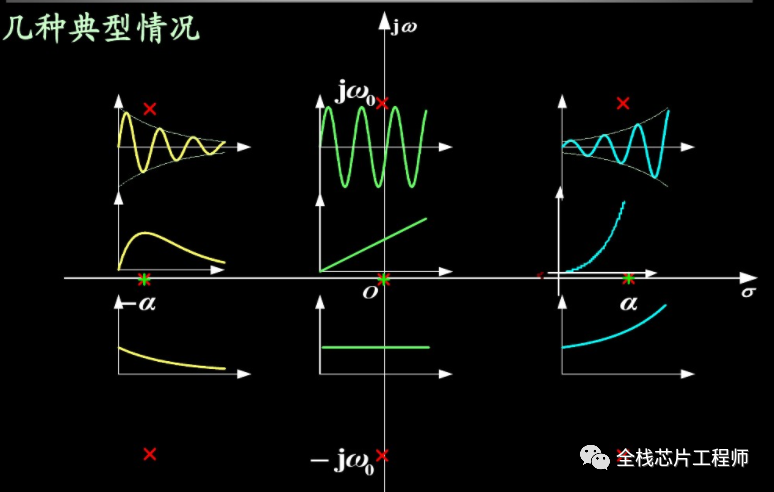
零点、极点分析
1、零点
零点:使系统传递函数G(s)为0的s的值,其中s为复数。比如:
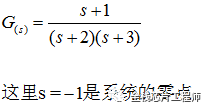
s=-1是零点。
2、极点
极点:使系统传递函数G(s)分母为0的s的值,其中s为复数。比如:
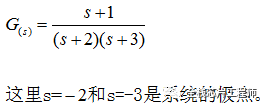
s=-2、s=-3是极点。
为何Z变换?
我们知道,傅里叶变换公示如下:
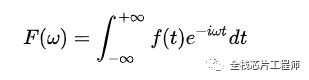
在函数收敛情况下,才可傅里叶变换,不收敛则乘以一个衰减函数形成拉普拉斯变换。
同样的,离散周期信号的傅里叶级数为:
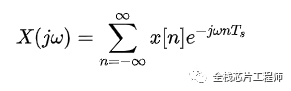

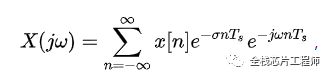
进一步化简:
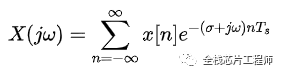
令:
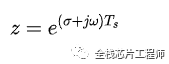
则DFT的表达式变为:这就是Z变换!!!
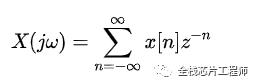
精采绝伦吗?继续high
由连续函数*衰减函数的傅里叶变换,即拉普拉斯变换,我们假定了:
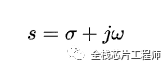
由离散函数*衰减函数的傅里叶变换,即Z变换,我们假定了:
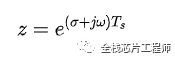
也就是说,z域和s域有如下关系:
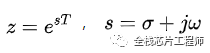


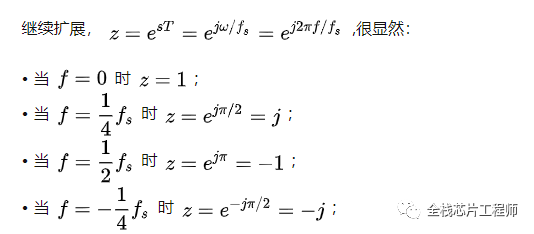
我们知道在s域上,虚轴上不同的点对应不同的频率,而z域上单位圆与s域虚轴对应,可见,z域单位圆上不同的点,代表了不同的频率。
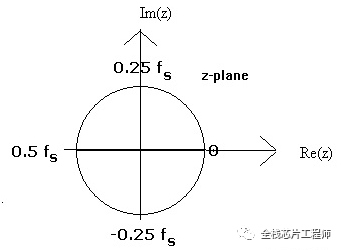
对于z域的传递函数的零极点,也有和s域零极点类似的结论:
规律1:如果在单位圆上有零点,则在零点所对应的频率上幅值响应为零;
规律2:对于不在单位圆上的零点,在单位圆上离零点最近的点对应的频率上幅值响应最小。
规律3:对于在单位圆内部的极点,在单位圆上离极点最近的点对应的频率上幅值响应最大。
规律4:如果极点和零点重合,对系统的频率响应没有影响。
零、极点影响频率响应
例子1:
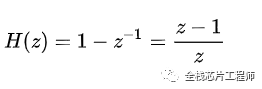
对于这个系统,在z=0有一个极点,在z=1时有一个零点。零、极点分布如下:
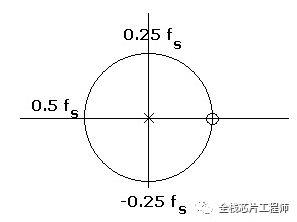
其中o表示零点,x表示极点。从z=1也就是单位圆上角度为零(也是频率为零)的点开始,此处z=1有一个零点,根据规律1,显然在频率为零时系统响应为零。
顺着单位圆沿逆时针方向旋转,我们离零点越来越远,零点的影响也越来越小,因此幅值响应会逐渐增大。当我们到达z=-1 ,也就是频率为1/2fs时,此时离零点最远,因此响应会达到一个最大值,当频率继续增大时,由于离零点又开始接近了,幅值响应又开始变小。
极点正好位于圆心位置,也就是说所有频率段离极点的距离都一样,因此可以认为都没影响。
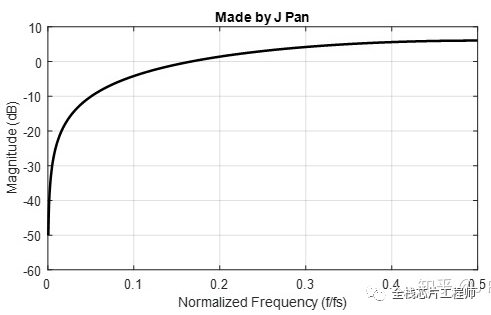
用freqz函数将系统的频响画出来,如下图,这个系统本质上是一个高通滤波器。
这个系统转换到时域:

是不是很惊喜,这本质就是一个差分,低频信号被过滤,高频信号通过。
这一个差分,对应连续系统的微分。我们知道微分对应的是传递函数是s,稳态时为s=jw,这显然是一个高通滤波器。
审核编辑 :李倩
-
傅里叶变换和拉普拉斯变换的关系是什么2024-02-18 3735
-
傅里叶变换和拉普拉斯变换的区别联系2023-09-07 4567
-
从傅里叶变换如何推换出拉普拉斯变换?2021-06-23 8327
-
傅里叶变换和拉普拉斯变换与Z变换到底有什么的联系和作用2021-02-15 9902
-
傅里叶变换与拉普拉斯变换的物理解释及区别pdf文档资料【下载】2017-12-19 1087
-
拉普拉斯变换及其逆变换表拉普拉斯变换及其逆变换表2017-12-05 265963
-
拉普拉斯变换及其应用_elecfans.com2015-10-28 1278
-
z变换与拉普拉斯变换的关系2009-09-30 1482
-
拉普拉斯变换与傅里叶变换的关系.ppt2009-09-16 4746
-
拉普拉斯变换的基本定理2009-07-27 26410
-
拉普拉斯变换课件教案2009-07-09 677
-
什么是拉普拉斯变换2009-07-08 7420
全部0条评论

快来发表一下你的评论吧 !

