1dB压缩点的定义

(一)非线性系统的模型

当信号幅度很小时，模拟和射频电路可以通过线性模型来近似，不过，小信号线性模型无法预测系统的非线性。

当需要考虑无记忆系统的非线性时，其输入/输出特性可以近似为：

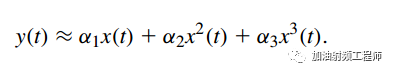
当信号很小时，后面两项可以忽略不计，因此此时，α1即为系统的小信号增益。

设：

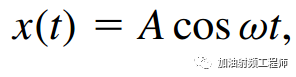
将上式代入输入/输出特性曲线，可得到：

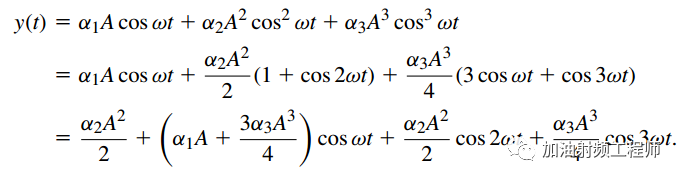
由上式可知，当输入为小信号时，系统的增益为

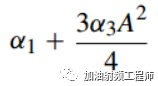
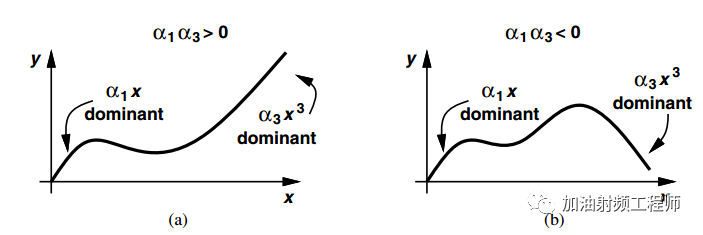
这边， α1 和α3的符号相反。

因为，如果α1 和α3的符号相同，则当信号足够大时，系统的增益也会变的很大，这是不现实的。

我们熟知的射频器件，比如说放大器等，在大信号输入时，增益都会压缩的。如下图所示。当 α1α3 < 0 时，信号x(t)=A cos ωt输入到系统后的增益随着 A 上升而下降。

(二) 1dB压缩点的定义

可以通过“1-dB 压缩点”来衡量增益下降的程度。

“输入1-dB 压缩点”定义为导致增益下降 1 dB 的输入信号电平，此时输出电平 Aout 在 1-dB 压缩点(Ain,1dB) 处低于其理想值 1dB。如下图所示。

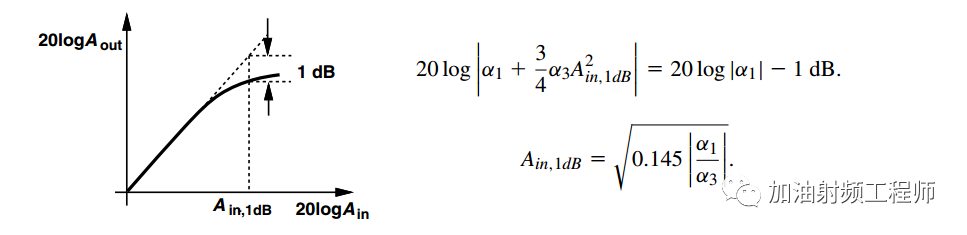
那1dB压缩点代表什么呢?

20log((0.89*A)/A)=-1dB。

所以,1dB压缩点代表系统增益下降约11%。

(三)系统增益压缩后的影响

系统增益压缩后，真的有关系么？

这要分情况讨论。

case1:

如果信号的幅度携带信息，那这个时候，信号会因压缩而失真，这个时候系统对增益压缩的容忍度是很低的。

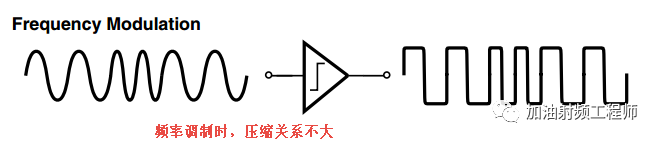
case2:

如果信号的幅度不携带信息(比如频率调制)，则可以容忍增益压缩。因为系统增益压缩了，代表输入信号足够大，接收机肯定能接收并解调出这个信号。

case3:

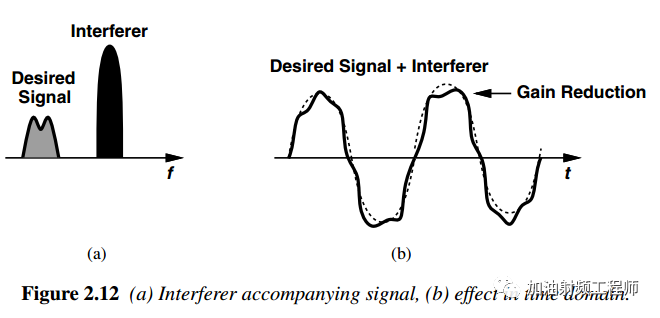
如果有用信号幅度比较小，但是旁边有比较大的干扰信号，如下图所示，这两个信号同时被接收机接收。这时，则会产生不利影响。

因为，虽然有用信号本身很小，但是因为干扰信号的存在，接收机的增益还是会被压缩。

这个时候，接收机的灵敏度会降低，即使在频率调制下也是如此。

（四）case3时的理论计算和仿真验证

那在case3时，到底会有多少影响呢？

假设，输入信号为：

经过一番推导，如下图所示：

所以，对于有用信号，其增益为：

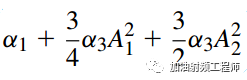
，因为A1<

对于干扰信号，其增益为：

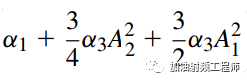
，因为A1<

所以 ，当 α1α3 < 0时，有用信号的增益和干扰信号的增益都会下降，但是下降的程度不太一样。

由下面的推导可知，当干扰信号的增益下降1dB时，有用信号的增益下降2.13dB。

现在用ADS进行仿真，看仿真值和理论计算值是否能吻合。

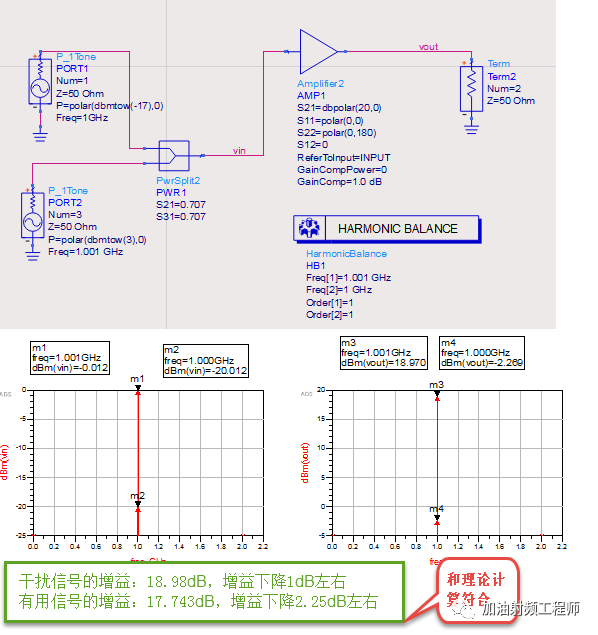
由上图仿真结果可知，仿真值和理论值符合。

当然，这也还只是仿真和理论值，如果要确认的话，还得实测。

有条件的朋友，可以在实验室搭个环境测试一下。

　　审核编辑：汤梓红