利用C语言实现高斯列主元消去法解线性方程组

这篇文章主要是用C语言实现高斯列主元消去法求解多元一次方程。

高斯列主元消去法

由于涉及到的数学公式太麻烦了，所以从网上找了一张图片，介绍高斯消去法的，如下图:

Gauss列主元素法

示例

假如现在有一个三元一次方程组，如下图：

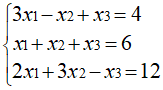
三元一次方程组

求解多元一次方程组可以分成三个步骤:

首先根据方程组构建增广矩阵

其次对增广矩阵经过行列式的初等变化变成上三角矩阵

最后从后往前回代求解。

构造增广矩阵

系数矩阵就是将方程组的系数组成矩阵。

而增广矩阵就是在系数矩阵的右边添上一列，这一列是线性方程组的等号右边的值。

下图即为行列式的增广矩阵：

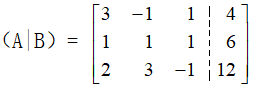
增广矩阵

组上三角矩阵

这里说的组上三角矩阵是指经过若干步初等变换，将矩阵左上角和右下角连线组成的对角线左下方的元素全部清零。

这个步骤主要涉及到主元以及初等变换两个概念。

主元指在消去过程中起主导作用的元素，主元通常选择绝对值最大的元素，用它做除法能够减小舍入误差的扩散，使得数值解比较可靠。

以下为行列式的初等变换：

换行变换:交换两行(列)

倍法变换:将行列式的某一行(列)的所有元素同乘以数k

消法变换:把行列式的某一行(列)的所有元素乘以一个数k并加到另一行(列)的对应元素上

而下面的图则是经过若干步初等变化组成的上三角矩阵:

迭代求解

在组成上三角矩阵之后，就可以从下往上依次回代求出方程的解了

C代码

#include
#include

#define MAX_MATRIX 10

/**
 * @brief SwapRow 进行行交换
 * @param m 待计算的矩阵
 *        row 待交行的行
 *        max_row 待交换的另一行
 *        n 矩阵行数
 */
static void SwapRow(double m[][MAX_MATRIX], int row, int max_row, int n) {
  double swap;
  for (int k = row; k <= n; k++) {
    swap = m[row][k];
    m[row][k] = m[max_row][k];
    m[max_row][k] = swap;
  }
}

/**
 * @brief 组上三角矩阵
 * @param m 待计算的矩阵
 *        n 矩阵行数
 */
static void SelectColE(double m[][MAX_MATRIX], int n) {
  int max_row_e = 0;  //主元所在行
  double ratio = 0;   //消元因数
  for (int j = 0; j < n; j++) {
    max_row_e = j;
    for (int i = j; i < n; i++) {
      if (fabs(m[i][j]) > fabs(m[max_row_e][j])) {
        max_row_e = i;
      }
    }
    if (max_row_e != j) {
      SwapRow(m, j, max_row_e, n);   //与最大主元所在行交换
    }
    //消元
    for (int i = j + 1; i < n; i++) {
      ratio = m[i][j] / m[j][j];
      for (int k = j; k < n + 1; k++) {
        m[i][k] -= m[j][k] * ratio;
      }
    }
  }
}

/**
 * @brief: Gauss 高斯列主元消元法求解线性方程(A*X = B)
 * @param: m 由于A|B组成的增广矩阵,X为待求的解
 *         n 求解的元数,n要小于MAX_MATRIX
 * @result:所求结果存放在m[][n]中
 */
void Gauss(double m[][MAX_MATRIX], int n) {
  SelectColE(m, n);   // 列选主元并消元成上三角
  // 回代求解,结果存在m[][n]中
  for(int i = n - 1; i >= 0; i--) {
    for(int j = i + 1; j < n; j++) {
      m[i][n] -= m[i][j] * m[j][n];
    }
    m[i][n] /= m[i][i];
  }
}

double a[3][MAX_MATRIX] = {
  {3,-1, 1, 4},  //A|B
  {1, 1, 1, 6},
  {2, 3,-1, 12}
};

int main(int argc ,char **argv) {
  Gauss(a, 3);
  printf("%f,%f,%f
",a[0][3], a[1][3], a[2][3]);
  return 0;
}

上述程序运行完成之后，终端输出：2.000000,3.000000,1.000000

审核编辑：郭婷