

三维点云配准的相关知识学习技巧
描述
1
点云配准过程就是求一个两个点云之间的旋转平移矩阵(rigid transform or euclidean transform 刚性变换或欧式变换),将源点云(source cloud)变换到目标点云(target cloud)相同的坐标系下。 可以表示为以下的方程:  其中
其中
 就是target cloud与source cloud中的一对对应点。 而我们要求的就是其中的R与T旋转平移矩阵。 这里,我们并不知道两个点集中点的对应关系。这也就是配准的核心问题。
就是target cloud与source cloud中的一对对应点。 而我们要求的就是其中的R与T旋转平移矩阵。 这里,我们并不知道两个点集中点的对应关系。这也就是配准的核心问题。
2
配准分为粗配准与精配准两步粗配准就是再两个点云还差得十万八千里、完全不清楚两个点云的相对位置关系的情况下,找到一个这两个点云近似的旋转平移矩阵(不一定很精确,但是已经大概是对的了)。 精配准就是在已知一个旋转平移的初值的情况下(这个初值大概已经是正确的了),进一步计算得到更加精确的旋转平移矩阵。 这里从精配准开始讲起。 精配准的模式基本上已经固定为使用ICP算法及其各种变种。ICP算法由Besl and McKay 1992, Method for registration of 3-D shapes文章提出。 文中提到的算法不仅仅考虑了点集与点集之间的配准,还有点集到模型、模型到模型的配准等。 简要介绍一下点集到点集ICP配准的算法:1) ICP算法核心是最小化一个目标函数:

(这里的表述与原文略微有些不同,原文是用四元数加上一个偏移向量来表达旋转平移变换。) 就是一对对应点,总共有
就是一对对应点,总共有 对对应点。这个目标函数实际上就是所有对应点之间的欧式距离的平方和。2) 寻找对应点可是,我们现在并不知道有哪些对应点。因此,我们在有初值的情况下,假设用初始的旋转平移矩阵对source cloud进行变换,得到的一个变换后的点云。 然后将这个变换后的点云与target cloud进行比较,只要两个点云中存在距离小于一定阈值(这就是题主所说的ICP中的一个参数),我们就认为这两个点就是对应点。这也是"最邻近点"这个说法的来源。3) R、T优化有了对应点之后,我们就可以用对应点对旋转R与平移T进行估计。这里R和T中只有6个自由度,而我们的对应点数量是庞大的(存在多余观测值)。因此,我们可以采用最小二乘等方法求解最优的旋转平移矩阵。一个数值优化问题,这里就不详细讲了。4) 迭代我们优化得到了一个新的R与T,导致了一些点转换后的位置发生变化,一些最邻近点对也相应的发生了变化。 因此,我们又回到了步骤2)中的寻找最邻近点方法。2)3)步骤不停迭代进行,直到满足一些迭代终止条件,如R、T的变化量小于一定值,或者上述目标函数的变化小于一定值,或者邻近点对不再变化等。(这里也是题主所说的ICP算法中的一个参数) 算法大致流程就是上面这样。这里的优化过程是一个贪心的策略。首先固定R跟T利用最邻近算法找到最优的点对,然后固定最优的点对来优化R和T,依次反复迭代进行。 这两个步骤都使得目标函数值下降,所以ICP算法总是收敛的,这也就是原文中收敛性的证明过程。这种优化思想与K均值聚类的优化思想非常相似,固定类中心优化每个点的类别,固定每个点的类别优化类中心。 关于参数的选择: ICP算法的参数主要有两个。一个是ICP的邻近距离,另外一个是迭代的终止条件。这些参数的选择,与实际的工程应用相关。比如说你的仪器精度是5mm,那么小于5mm是可以认为是对应点,而最终的迭代终止条件也就是匹配点之间平均距离小于5mm。 而且这些参数可以由算法逐步迭代减小,最初使用较大的对应点距离参数,然后逐步减小到一个较小的值。(问过师兄才知道实际过程这样操作会比较合适。)需要手动调整一些参数。(这跟机器学习调参比起来,简直不是事~)
对对应点。这个目标函数实际上就是所有对应点之间的欧式距离的平方和。2) 寻找对应点可是,我们现在并不知道有哪些对应点。因此,我们在有初值的情况下,假设用初始的旋转平移矩阵对source cloud进行变换,得到的一个变换后的点云。 然后将这个变换后的点云与target cloud进行比较,只要两个点云中存在距离小于一定阈值(这就是题主所说的ICP中的一个参数),我们就认为这两个点就是对应点。这也是"最邻近点"这个说法的来源。3) R、T优化有了对应点之后,我们就可以用对应点对旋转R与平移T进行估计。这里R和T中只有6个自由度,而我们的对应点数量是庞大的(存在多余观测值)。因此,我们可以采用最小二乘等方法求解最优的旋转平移矩阵。一个数值优化问题,这里就不详细讲了。4) 迭代我们优化得到了一个新的R与T,导致了一些点转换后的位置发生变化,一些最邻近点对也相应的发生了变化。 因此,我们又回到了步骤2)中的寻找最邻近点方法。2)3)步骤不停迭代进行,直到满足一些迭代终止条件,如R、T的变化量小于一定值,或者上述目标函数的变化小于一定值,或者邻近点对不再变化等。(这里也是题主所说的ICP算法中的一个参数) 算法大致流程就是上面这样。这里的优化过程是一个贪心的策略。首先固定R跟T利用最邻近算法找到最优的点对,然后固定最优的点对来优化R和T,依次反复迭代进行。 这两个步骤都使得目标函数值下降,所以ICP算法总是收敛的,这也就是原文中收敛性的证明过程。这种优化思想与K均值聚类的优化思想非常相似,固定类中心优化每个点的类别,固定每个点的类别优化类中心。 关于参数的选择: ICP算法的参数主要有两个。一个是ICP的邻近距离,另外一个是迭代的终止条件。这些参数的选择,与实际的工程应用相关。比如说你的仪器精度是5mm,那么小于5mm是可以认为是对应点,而最终的迭代终止条件也就是匹配点之间平均距离小于5mm。 而且这些参数可以由算法逐步迭代减小,最初使用较大的对应点距离参数,然后逐步减小到一个较小的值。(问过师兄才知道实际过程这样操作会比较合适。)需要手动调整一些参数。(这跟机器学习调参比起来,简直不是事~)
3
粗配准前面介绍到了,ICP算法的基本原理。它需要一个旋转平移矩阵的初值。这个初值如果不太正确,那么由于它的greedy优化的策略,会使其目标函数下降到某一个局部最优点(当然也是一个错误的旋转平移矩阵)。因此,我们需要找到一个比较准确的初值,这也就是粗配准需要做的。 粗配准目前来说还是一个难点。针对于不同的数据,有许多不同的方法被提出。 我们先介绍配准的评价标准,再在这个标准下提出一些搜索策略。 评价标准:比较通用的一个是LCP(Largetst Common Pointset)。给定两个点集P,Q,找到一个变换T(P),使得变换后的P与Q的重叠度最大。在变换后的P内任意一点,如果在容差范围内有另外一个Q的点,则认为该点是重合点。重合点占所有点数量的比例就是重叠度。 解决上述LCP问题,最简单粗暴的方法就是遍历。假设点集P,Q的大小分别为m,n。而找到一个刚体变换需要3对对应点。 那么brute force 搜索的需要的复杂度。对于动辄几百万个点的点云,这种时间复杂度是不可接受的。 因此,许多搜索策略被提出。比较容易想到的是RANSAC之类的搜索方法。而对于不同的场景特点,可以利用需配准点云的特定信息加快搜索。(例如知道点云是由特定形状的面构成的)这里先介绍一个适用于各种点云,不需要先验信息的搜索策略,称为4PC(4 Point Congruent)。 搜索策略:4PC搜索策略是在P,Q中找到四个共面的对应点。
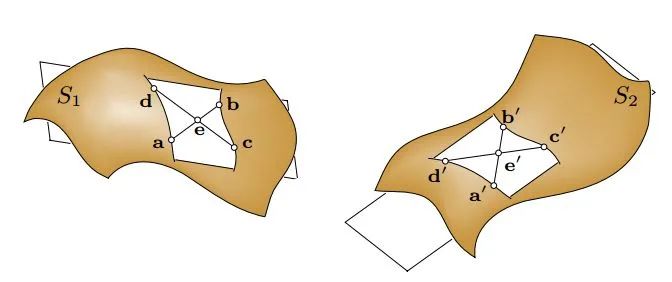
如上图所示(来自4PC原文),这四个共面的点相交于e。这里有两个比例在刚体变化下是不变的。(实际上在仿射变换下也是不变的) 
 而4PC将对于三个点的搜索转换为对e,e'的搜索,从而将复杂度降低到了
而4PC将对于三个点的搜索转换为对e,e'的搜索,从而将复杂度降低到了 。 这四个点的距离越远,计算得到的转换越稳健。但是这里的四个点的搜索依赖于两个点云的重叠度。 具体的算法可以参考4-Points Congruent Sets for Robust Pairwise Surface Registration的原文。 4PC算法通用性较好,但是对于重叠度较小、或是噪声较大的数据也会出现配准错误或是运行时间过长的问题。针对于不同的场景很多其他的搜索策略也被提出。 这里安利一下我师兄的论文吧~Automatic registration of large-scale urban scene point clouds based on semantic feature points 我们课题组主要是研究室外地面站LiDAR获取的点云配准问题。这种情形下,由于扫描仪内有自动安平装置,Z轴都是竖直方向(重力方向),刚体变换只存在三维平移与平面(XoY面上的)旋转。我们就在场景中搜索竖直的特征线并且得到它们与地面的交点。
。 这四个点的距离越远,计算得到的转换越稳健。但是这里的四个点的搜索依赖于两个点云的重叠度。 具体的算法可以参考4-Points Congruent Sets for Robust Pairwise Surface Registration的原文。 4PC算法通用性较好,但是对于重叠度较小、或是噪声较大的数据也会出现配准错误或是运行时间过长的问题。针对于不同的场景很多其他的搜索策略也被提出。 这里安利一下我师兄的论文吧~Automatic registration of large-scale urban scene point clouds based on semantic feature points 我们课题组主要是研究室外地面站LiDAR获取的点云配准问题。这种情形下,由于扫描仪内有自动安平装置,Z轴都是竖直方向(重力方向),刚体变换只存在三维平移与平面(XoY面上的)旋转。我们就在场景中搜索竖直的特征线并且得到它们与地面的交点。
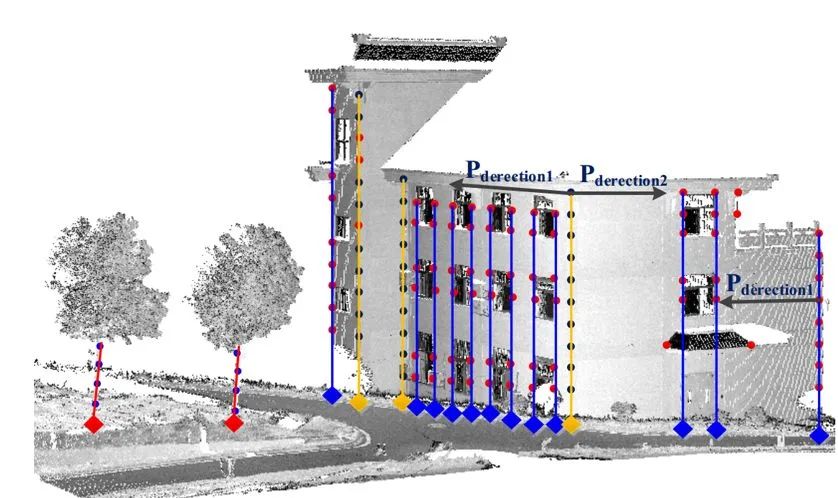
再将这些交点构建出三角形,以三角形的全等关系来得到匹配。
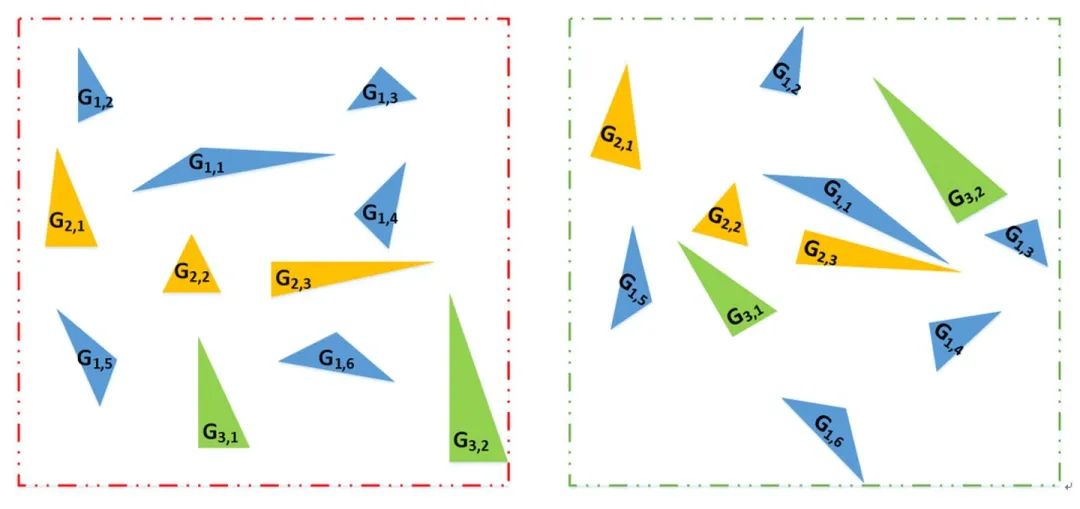
找出其中一致性最好的三角形集合,作为匹配的集合,进行粗配准。 这种方法适用于竖直线较多的场景,比如城区的建筑物的边线、林区树木的树干等。设计的方法还是很巧妙的。当然如果场景内这种特征较少,就比较难以配准。
参考文献
[1] Besl P J, Mckay N D. Method for registration of 3-D shapes[C]// Robotics - DL tentative. International Society for Optics and Photonics, 1992:239-256. [2] Aiger D, Mitra N J, Cohen-Or D. 4-points congruent sets for robust pairwise surface registration[J]. Acm Transactions on Graphics, 2008, 27(3):85. [3] Yang B, Dong Z, Liang F, et al. Automatic registration of large-scale urban scene point clouds based on semantic feature points[J]. Isprs Journal of Photogrammetry & Remote Sensing, 2016, 113:43-58.
-
三维快速建模技术与三维扫描建模的应用2018-08-07 3874
-
基于二维激光测距仪的三维模型配准研究2013-09-16 1260
-
一种快速的三维点云自动配准方法2013-09-23 708
-
三维颅骨自动非刚性配准方法2017-12-09 634
-
基于分层策略的三维非刚性模型配准算法2019-01-23 1353
-
计算机视觉:三维点云数据处理学习内容总结2020-11-27 5628
-
基于深度学习的三维点云语义分割研究分析2021-04-01 1334
-
点云的概念以及与三维图像的关系2021-08-17 8397
-
基于深度学习的三维点云配准方法2022-11-29 2381
-
基于深度学习的三维点云配准新方法2023-06-17 2176
-
三维场景点云理解与重建技术2023-08-08 2343
-
三维点云配准过程详解:算法原理及推导2023-09-21 2083
-
三维点云配准算法原理及推导2023-09-25 1732
-
AI 驱动三维逆向:点云降噪算法工具与机器学习建模能力的前沿应用2025-08-20 503
全部0条评论

快来发表一下你的评论吧 !

