

关于采样率,您真正需要了解的内容
描述
总的来说,对采样率的讨论就像看着油漆变干。我们真的需要深入了解细节吗?毕竟,每个人都知道,您只需要以目标信号频率的两倍进行采样即可获得良好的结果,对吧?如果你对最后一句话的回答是“对!”,也许你应该继续读下去。虽然所谓的奈奎斯特速率(即最高信号频率分量的两倍)确实是消除混叠频率所需的采样速率,但该规则经常被忽视的限定符是,被数字化的信号必须被带宽限制在等于奈奎斯特速率一半的值。重要的不仅仅是您感兴趣的频率,还有您数字化的信号中包含的所有频率以及它们与您选择的采样率的比较情况。让我们回到基础。
什么是别名频率?
韦伯斯特将“别名”定义为假名或附加名称。出于数据采集的目的,我们可以更准确地将别名定义为假定频率或附加频率。
在观看超速行驶的汽车的电影时,您看着汽车的车轮,它们似乎旋转得不可思议,甚至向后旋转。您看到的是由汽车车轮的快速旋转速率与用于记录图像的相机的慢得多的帧速率之间的数学碰撞引起的混叠频率。你下意识地从对图像的解释中过滤掉这种异常,因为从其他参考系中很容易确定汽车正在高速前进。但是,如果您正在观看一部关于汽车车轮的电影呢?在这种情况下,如果被要求确定汽车移动的速度和方向,你可能会得出一个完全不同的、错误的和令人尴尬的结论。
扩展上面的例子,您可以将相机视为数据采集系统,将旋转轮视为它正在数字化的信号。如果数据采集系统的采样速率相对于信号频率太慢,您的测量就会崩溃。你没有电影的方便参考框架。您所拥有的只是随时间变化的信号幅度的集合。哪些是真实的,哪些是别名?就像试图通过只看车轮来解释电影中汽车的运动一样,这是不可能知道的,而且你的测量值有太多的东西无法猜测。
别名频率的数学
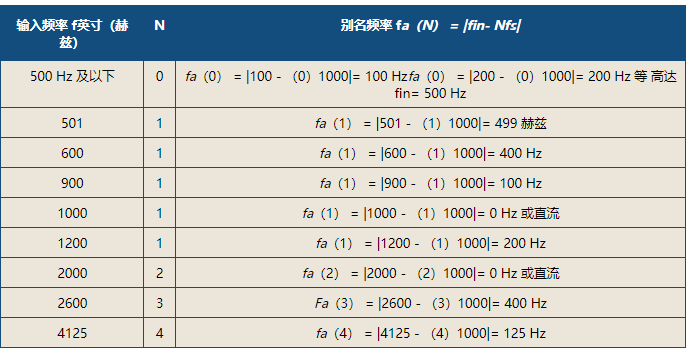
如果我们知道输入信号的频率和采样率,我们可以预测混叠频率。公式(1)表明,混叠频率是输入信号频率与采样率的最接近整数倍之差绝对值的函数。

让我们用一些例子来扩展这个等式。表1是以1000 Hz的固定速率采样的各种正弦输入信号频率(fin)以及使用公式(1)计算得出的混叠频率的汇编。常数 (N) 是一个整数,它假定使项 Nfs最接近输入信号频率 (fin) 所需的值。例如,如果输入频率为 150 Hz,采样率为 75 Hz,则 N等于 2。如果输入信号频率增加到 188 Hz,N 将变为3,因为 75 和 3 (225) 的乘积比 75 和 2 (150) 的乘积更接近 188。
从表1可以看出,任何小于或等于500 Hz奈奎斯特值(采样率的一半)的输入信号频率都会被准确再现。任何大于此值的频率都会产生不准确的混叠频率,甚至在输入频率是采样速率的精确倍数时再现直流信号的程度也是如此。显然,当输入信号的频率成分超过采样率的一半时,所有的赌注都是错误的。
表 1:固定 1000 Hz 采样率下的混叠与输入频率的关系
混叠频率是什么样的?这是阴险的事情。它看起来就像真实数据一样。如果我们按照表(1)中所述的方式采集数据,当fin等于900 Hz时,我们会看到图1所示的灰色100 Hz别名波形,而不是实际连接到数据采集系统的黑色900 Hz波形。除了较低的频率,你能分辨出真实信号和鬼影之间的区别吗?更复杂的是,我们大多数人不会四处奔波获取纯正弦波。典型的波形是许多频率的复杂组合,而混叠的录制波形可能看起来非常合理,但会导致您得出完全错误的结论。
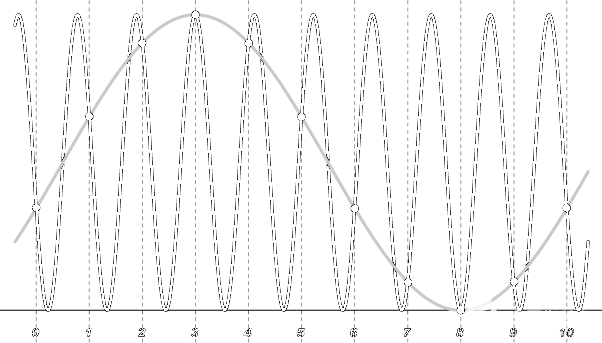
图1 - 900 Hz波形(黑色)在1000 Hz采样不足时产生混叠的100 Hz波形(灰色)
解决方案是什么?
回到本应用笔记开始的地方,只有确保信号中不存在高于此限值的其他频率分量,我们才能满足奈奎斯特采样率准则,即目标最大信号频率的两倍。除非我们对信号源的频率成分有高度的置信度,否则达到这一条件的唯一方法是在数字化之前将输入信号应用于低通抗混叠滤波器。对抗混叠滤波器的深入讨论超出了本应用笔记的范围,但其显著特性可归纳如下:
低通设计
选择转折频率以达到您感兴趣的最大频率(即采样率的一半)
从通带到阻带的陡峭过渡带滚降。
图2是上述理想抗混叠滤波器的图形表示。请注意,在实际滤波器设计中,过渡带的理想垂直形状是不可能的,而是会产生带有一些负斜率的滚降。这种现实迫使以较低的转折频率或较高的采样率的形式进行折衷。例如,人耳可以响应高达 20 kHz 的频率。如果可以使用符合理想的抗混叠滤波器,则可以使用40 kHz的采样率对音乐进行数字化。然而,44.1 kHz的标准速率既反映了滤波器实现不理想的现实,也反映了保持20 kHz完整响应的愿望。
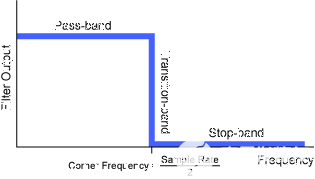
图2 - 理想抗混叠滤波器的图形表示。
您真的需要抗锯齿过滤器吗?
该领域的权威人士坚持认为,在没有抗锯齿滤波器的情况下获取的数据是无用的。这些人可能会坚持让你系安全带只是为了把车开进车库,因为“安全带可以挽救生命”。事实上,在日常测量中采集的大部分数据不需要抗混叠滤波器来产生完全准确和可操作的结果,这就是为什么绝大多数数据采集和数据记录仪仪器不会在每个测量通道中内置一个。任何不同意这种说法的人都应该问问自己是否需要滤波器来测量电池电压 - 纯 0 Hz。如果没有,那么我们至少已经打开了妥协的大门,我们可以进一步打开它,包括其他直流或近直流信号的测量:温度、湿度、直流电流、流量、压力、负载、扭矩、频谱图、GSR、平滑和骨骼肌浴等。那么频率成分被明确定义和包含的信号呢:50/60/400 Hz 电压和电流、血压和流量,甚至一些生物电位,如 ECG 和 EMG?我们开始覆盖许多测量领域,而无需过滤器。还有更多的例子,但过滤器确实有其位置。
基于加速度计的测量是抗混叠滤波器几乎需要的最佳示例。大多数压电加速度计的频率响应超过15 kHz。尽管您感兴趣的频率可能远低于此频率(例如,由于轴承磨损而导致的 40 Hz 电机隆隆声),但您不能忽视传感器可以并且将会通过更高频率的事实。如果你已经读到这里,你应该知道,仅仅因为你对40 Hz以上的频率不感兴趣并不意味着你只需要在80 Hz左右采样,如果传感器可以通过更高几个数量级的频率。
您可能需要过采样
到目前为止,我们已经看到,带宽受限的输入信号以至少两倍于抗混叠滤波器转折频率的速率采样,可以再现输入信号的频率成分。如果您只对被测系统的频率内容感兴趣,并且有些应用是分析的范围,那就太好了。回到加速度计的例子,你真的不在乎波形是什么样子的,因为它是频谱来传达电机隆隆声的存在和频率。但是对于波形形状确实传达信息的其他应用,祝你好运,每个周期从两个样本中提取信息。参考图1所示的100 Hz混叠波形,您甚至无法仅用两个点远程重建正弦波。每当您需要精确的波形再现时,您唯一的办法就是以超过奈奎斯特最小值 2 倍(通常为 10 倍或更多)的速率进行过采样。假设您已经准确地考虑了信号的频率内容并消除了混叠频率的可能性,则您选择的实际倍数由个人喜好决定。
审核编辑:郭婷
-
如何优化adc的采样率2024-10-31 2486
-
USB 3.2双通道操作:您需要了解的内容2024-08-30 584
-
adc采样率和带宽的关系2023-09-12 20116
-
什么叫采样率 数字信号处理时钟与采样率的关系2023-08-17 6522
-
什么是信号采样率?如何更改信号的采样率?2023-06-20 5397
-
做好准备:关于 ESD 和 RF 设备您需要了解什么2022-12-26 2213
-
嵌入式主板真正需要做什么2021-12-16 849
-
关于电池管理,您需要了解的内容2021-05-12 638
-
关于1Gsa/s采样率的介绍研究2019-10-10 21797
-
什么是消费者真正需要的物联网产品2018-07-18 4602
-
差分对:你真正需要了解的内容2015-09-03 6192
-
正需要这些,楼主辛苦了!!!2013-04-18 3977
-
示波器的采样率和存储深度2009-08-24 7726
全部0条评论

快来发表一下你的评论吧 !

