数据采集参数的设置方式使ADC分辨率低于总线

每个人都同意更高分辨率的模数转换器（ADC）更好，对吧？那么，为什么这么多最终用户为一个用户掏钱，然后却没有利用这一优势呢？我的意思是，当我们从客户那里收到数据文件时，我们经常感到震惊，其中数据采集参数的设置方式使ADC分辨率低于总线。一个例子可能会有所帮助，这里只是众多例子中的一个（客户将永远保持无名）：

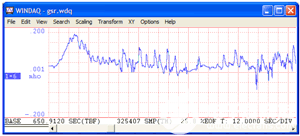
图1 — 客户通常查看的渠道数据看起来正常。

图 1 是从WinDaq回放软件查看的WinDaq 获取数据的屏幕截图。波形是用14位ADC采集的。看起来还行吧？啊，但我让你处于劣势。客户垂直缩放了跟踪，只提供一切良好的错觉。事实上，这个渠道是以我们亲切地称之为“在泥泞中”的方式获得的。

利用名为“显示动态范围”的WinDaq功能（见图 2），我可以强制所选通道自动缩放，以适应 ADC 测量范围的上限和下限，以提供 ADC 在数字化通道数据时看到的直观图像。

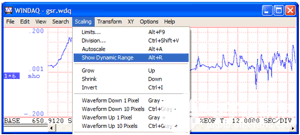
图 2 — 调用 WinDaq 的“显示动态范围”函数讲述真实情况

结果是图3，走线几乎消失，这意味着ADC没有太多信号可以使用（即信号“在泥泞中”）。

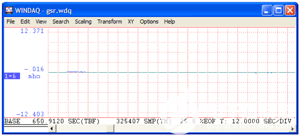
图 3 — 这是 ADC 看到的 WinDaq 的显示动态范围功能所显示的内容。

那么，问题出在哪里呢？

您可以将在满量程范围如此小的百分比下采集数据视为ADC分辨率的有效降低，我们可以用数学方式描述这种降低，本质上是反向工作以确定ADC的有效位分辨率。

我们可以首先定义一个方程，将ADC计数与ADC的分辨率（假设为双极性范围）以及满量程信号和ADC范围的比值（以工程单位表示）：

　　

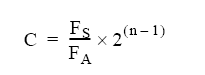
　　等式 1 其中：

　　C = 应用于测量的 ADC 计数。

　　F S = 以工程单位表示的满量程信号范围 FA = 以工程单位

　　表示的满量程 ADC 范围 n= ADC 位分辨率

　　从公式（1）可以看出，如果信号的满量程范围（F S）小于ADC的满量程范围（F A），则应用于测量的ADC计数将减少比率FS：FA。如果FS等于FA，则所有ADC计数都应用于测量，这是理想情况。在这种情况下，公式（1）简化为：

　　

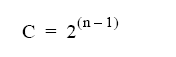
　　等式2

　　接下来，我们可以代数操作方程（2）来求解n，因为我们对ADC在FS

　　

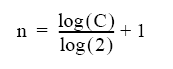
　　等式3

等式（3）基本上扭转了分辨率问题。给定根据公式（1）计算出的信号，其偏移仅为C ADC计数，公式（3）描述了处理该信号所需的ADC的有效位分辨率。

将一切整合在一起

让我们看看数学如何在客户数据文件的上下文中进行排序。我们将首先使用公式 （1） 计算 C。

从WinDaq回放软件的统计功能中，我可以很容易地确定：FS = 0.171 mho

从图 3 中，我可以看到WinDaq显示的满量程动态范围为：FA= 12.371 mho

我们还知道，测量是使用14位双极性ADC进行的。现在我们有足够的信息来确定使用公式（1）测量的总ADC计数：

 

现在，我几乎可以肯定，如果我们的客户在购买ADC数据手册之前查看了它，并看到其分辨率低于8位，他会立即转向其他供应商。然而，通过以他的方式获取数据，这就是他对测量的所有分辨率。不要陷入陷阱，认为他只遭受了44%的惩罚（14到7.84位）。请记住，ADC计数与位分辨率呈指数相关。事实上，我们的客户遭受了超过 98% 的性能影响：2 14 到 27.82，或16384到 226 ADC 计数。哎哟！

获得救援

那么如何解决这一困境呢？客户以 1 的增益因子获取了我们的示例数据文件，但他用于执行此操作的仪器也允许应用 10 和 100 的可编程增益因子。应用大于 1 的增益因数会影响将 ADC 的满量程范围（公式 （1） 中的变量 F A降低等于增益因数的倒数乘以 FA。图灵到我们的示例计算，如果客户以10的增益获取信号（增益为100太大，会使FS>FA），则应用于测量的总ADC计数将为：

 

 

应用10的增益因数可有效地将ADC位分辨率从7.82位提高到11.15位。就所有重要的ADC计数而言，这提高了近900%。

结论

本应用笔记的重点并不是说在获取数据之前需要浏览方程。提供这些只是为了强调以下论点：在ADC满量程范围的极低百分比下采集的信号在有效ADC位分辨率方面会受到严重的性能影响。您的经验法则应该是确保您希望获取的信号的预期满量程偏移至少消耗ADC满量程范围的一半。如果没有，则利用大多数中到高性能数据采集硬件产品中内置的增益功能。

最后，为了您的方便，我准备了表（1），以便快速查看您在各种FS：FA比率下将遭受的性能影响（作为ADC分辨率的函数）。明智地使用它。

FS/FA	本机 ADC 分辨率	性能影响 （%）
8 位	10 位	12 位	14 位	16 位
有效的ADC分辨率（ne)
1.00	8.0	10.0	12.0	14.0	16.0	0
0.90	7.8	9.8	11.8	13.8	15.8	10
0.80	7.7	9.7	11.7	13.7	15.7	20
0.70	7.5	9.5	11.5	13.5	15.5	30
0.60	7.3	9.3	11.3	13.3	15.3	40
0.50	7.0	9.0	11.0	13.0	15.0	50
0.40	6.7	8.7	10.7	12.7	14.7	60
0.30	6.3	8.3	10.3	12.3	14.3	70
0.20	5.7	7.7	9.7	11.7	13.7	80
0.10	4.7	6.7	8.7	10.7	12.7	90

表 1 - 性能影响衡量可用 ADC 计数的减少与峰值信号与满量程 ADC 范围之比的函数关系。